基于Python实现的Apriori算法和FP-Growth算法的频繁项集挖掘的研究与实现
摘 要
随着科技的快速发展和存储技术的飞速提升,使得我们生活在了数据的海洋,各行各业都积累着海量数据。我们如何利用这些数据,发掘出隐藏在其中的有价值的信息是数据挖掘诞生的重要因素。上世纪90年代,沃尔玛在其海量交易数据中发现了经典的“啤酒与尿布的故事”,揭示了美国人的某种购物习惯,并根据该特点调整布局,利润大幅提升,该过程被称作“购物篮分析”。这是数据挖掘早期在实际应用中的成功案例,也是频繁项集挖掘的起源。
现如今,人们越来越重视隐藏在海量数据下的潜在价值,数据挖掘技术不断被运用到互联网、电信、金融、商业等领域。其中,频繁项集挖掘技术在商业领域的运用成为重要的研究课题。
以下是本篇论文的主要内容:
- 对频繁项集挖掘的有关概念以及理论做了具体的阐述;
- 详细介绍两类最经典的频繁项集挖掘算法:apriori算法和fp-growth算法;
- 分别实现这两个算法,详细介绍apriori如何迭代生成所有的频繁项集,fp-growth的fp-tree的构造过程以及如何通过fp-tree发掘频繁项集,根据频繁项集计算关联规则,对算法运行结果加以分析。
- 对比分析apriori算法和fp-growth算法各自的优缺点及适用场景。
关键词:数据挖掘;Apriori算法;FP-Growth算法;购物篮分析
Abstract
With the rapid development of science andtechnology and the rapid improvement of storage technology, we have been livingin the ocean of data, and all trades and professions are accumulating hugeamounts of data. How to use these data to discover valuable information hiddenin it is an important factor in the birth of data mining. In the 90s of lastcentury, WAL-MART found the classic "story of beer and diaper" in itsmassive transaction data, revealing some of the Americans' shopping habits, andadjusting their distribution according to the characteristics. The profit wasgreatly improved. The process was called "shopping basket analysis".This is a successful case in the early application of data mining, and also theorigin of frequent itemsets mining.
Nowadays, people pay more and more attentionto the potential value hidden under mass data. Data mining technology has beenused in the fields of Internet, telecommunications, finance, commerce and soon. Among them, the application of frequent itemsets mining technology in thecommercial field has become an important research topic.
The following is the main content ofthis paper:
- the concepts and theories offrequent itemsets mining are elaborated.
- introduce two kinds of classicfrequent itemsets mining algorithm: Apriori algorithm and FP-growth algorithm.
- the two algorithms are implementedin detail, in detail, how Apriori iteratively generates all the frequentitemsets, the construction process of FP-growth FP-tree and how to discoverfrequent itemsets through FP-tree, and calculate the association rulesaccording to the frequent itemsets, and analyze the results of the algorithm.
- comparative analysis of theadvantages and disadvantages of Apriori algorithm and FP-growth algorithm andits application scenarios.
Keywords: Data mining; Apriori algorithm; FP-Growth algorithm; Shopping basket analysis
第一章 绪论
1.1 选题背景与研究意义
互联网的发展让我们处在了一个信息时代,人们的生产生活越来越离不开信息资源,并且时时刻刻也在产生更多的数据,数据规模不断地增长,自从数据存储技术逐渐成熟之后,数据的计量单位也不只是从前的B、KB、MB、GB、TB,如今我们不得已使用更大的单位,比如PB、EB、ZB、YB、BB等等来衡量这不断增长的数据,并且不仅仅是数据量,数据的种类也很繁多,数据中所蕴藏的价值也是难以估量的。倘若我们依然使用传统的数据分析工具或使用我们的大脑来分析这些数据只能是管中窥豹,只见一斑,这就造成了信息过载。目前,数据存储技术以及互联网的发展程度使得数据的采集和存储已经不再是难题。而如何从如此庞大的数据中挖掘出人们感兴趣的信息,进而来预测未来事务的发展导向,提供决策支持,才是摆在人们面前的首要问题。
显然,人们早已意识到了数据挖掘的重要性,并且许多的人已经投入到数据挖掘与机器学习的研究中,并且我们也已经从中受益,越来越多的成果进入我们的生活,比如搜索引擎,个性化推荐等,不仅仅是互联网业、制造业、金融业、零售、电商、生物工程等等,无处不在。而最贴近人们生活的,还应当属数据挖掘在电商以及零售业的运用。通过对消费者的购买记录进行分析,发掘出人们的某种购买共性,从而精确的进行产品推荐、折扣促销、广告投放、商品陈列布局的调整等等一系列的措施来实现销量的提升,当年沃尔玛“啤酒与尿布”的故事被传为佳话,现如今,淘宝,京东等电商的个性化推荐定位精确。
基于以上背景,该论文对频繁项集挖掘算法进行深入学习和钻研,并且实现了Apriori算法和Fp-growth算法,理解频繁项集的产生过程,推导出关联规则,并使用真实的购物数据对算法进行检验,对两种算法的效率进行比较,分析各自的特点。
1.2 应用领域
目前,随着数据挖掘及相关技术的成熟,数据挖掘已经应用到各行各业,关联分析作为数据挖掘的主要研究课题之一,早已经融入我们的生活。
现代经济社会中,很多行业,比如农业、旅游业等都与天气变化息息相关,人们对气象信息的需求越来越大,对气象信息的准确度要求也越来越高,而目前我们已经拥有了近60年的中国地面气象历史数据,运用数据挖掘技术,提升气象数据处理的质量,准确建立气象预测模型,助力现代经济的发展,提升人们的生活品质。
随着会联网的发展,越来越多的人将阅读对象从传统的书刊报纸转向在线阅读,诸多新闻类门户网站迅速兴起,例如网易新闻、今日头条等。研究表明,同一用于所浏览的不同新闻之间存在着内容上的某些关联,因此,我们希望标记出用户的浏览兴趣和规律,做及时准确的预测及推荐。
在金融行业中,关联规则挖掘也有广泛的应用,银行可以用它来分析客户的需求,调整自身的产品推广方案。举个例子,假设某人更换了在银行的预留地址,我们可以预测它大概是更换了一套更大的房子,于是他将需要更高的额度限制,或者需要申请房贷车贷等,于是银行可以根据这些数据,预测出用户的兴趣。
自古有神农尝百草,华佗悬壶济世,中医在经过了几千年的历史积淀,成为了我国文化瑰宝。但是到目前为止,中医的望闻问切依然是全凭经验,具有很强的主观性,缺乏系统的归纳和统计,这使得中医的发展被制约。因而,使中医由前人经验变为有理有据的现代医学已经是大势所趋。目前,我们已经积累了大量地医学数据,可以合理的利用这些数据,挖掘出病症与病理之间的联系,为医生提供诊断辅助和决策帮助,目前数据挖掘在该领域取得了了不少研究成果。
频繁项集挖掘技术不仅仅是应用在商业分析中,在其他领域比如建筑,医疗,电信,保险等等,都有广泛应用,而且取得了丰硕的成果。
1.3 主要研究内容
本文研究了频繁项集挖掘算法,主要针对电商或者超市的销售数据,分析用户的购买行为,发现隐藏其中的关联关系,为商家提供决策支持。具体工作如下:
-
搜集数据,主要针对超市或电商的销售的订单数据。
-
编程实现Apriori算法,并使用它挖掘出实验数据中的频繁模式。
-
编程实现Fp-growth算法,用同样的支持度和置信度对实验数据进行挖掘。
-
比较Apriori算法与Fp-growth算法,检验二者的运行结果是否一致,并且阐述了两种算法的各自的特点。
-
根据生成的频繁模式寻找关联关系,根据最小置信度找出强关联规则,对结果进行分析。
1.4 论文组织结构
本文有五个章节组成,组织结构如下:
-
第一章 绪论:该章节介绍了毕业设计的选题背景与研究意义,毕业设计所做的主要工作和论文的组织结构。
-
第二章 理论基础:该章节介绍了什么是数据挖掘,并论述了数据挖掘的一般过程,对选题的频繁项集挖掘做了重点介绍,详细介绍了频繁项集和关联规则的知识,还对数据的预处理过程进行论述。
-
第三章 算法实现:该章节分别介绍了Apriori算法和Fp-growth算法,详细介绍了算法原理以及实现过程,演示了如何构造Fp树以及挖掘频繁项集。
-
第四章 挖掘关联规则:本章根据前两章挖掘出的频繁项进行关联规则的挖掘,并计算规则的可信度,求出强关联。并且对两种算法进行了性能比较,阐述了各自的特点和缺陷,适应哪些场景等。
-
第五章 总结与展望:本章总结了毕业设计的所有工作,分析了工作中的不足,并且提出了解决方案。
第二章 理论基础
2.1 数据挖掘
数据挖掘(datamining),又名数据勘探、数据采矿,是指从大量数据中通过算法挖掘出隐藏其中的有价值的信息的一般过程,数据挖掘技术的发展离不开数据库技术的成熟,故又称数据挖掘为数据库中的知识发现。数据挖掘是一门交叉学科,通常与计算机科学有关,并涉及神经网络、遗传算法、回归、统计分析、机器学习、聚类分析等诸多方法来实现。
数据挖掘的一般过程分为数据收集、数据集成、数据规约、数据清理、数据转换、数据挖掘、模式评估和知识表示等八个步骤。
-
信息收集:分析所要挖掘的事务,抽象出有用的属性,构造相应数据集。现实应用中,数据都是海量的,合理的数据存储和管理方式至关重要。
-
数据集成:将搜集来的杂乱数据集成在一起,实现同构。
-
数据规约:由于数据挖掘在显示应用中的数据量一般都很大,执行时间过长,数据规约可以将数据集进行规约表示,此时数据量会大幅度缩小,并且挖掘的结果和规约前高度相同。
-
数据清理:由于数据集中某些数据不完整,或者某些数据包含错误属性,因此需要进行数据清理,将完整的、正确的,格式统一的数据数据保留。
-
数据转换:将数据转换成适用于数据挖掘的形式。
-
数据挖掘:分析数据特征,选择相符合的算法构建恰当的模型,挖掘出有用信息。
-
模式评估:由行业专家来验证结果的准确性。
-
知识表示:将数据挖掘的结果可视化供。
其中,数据集成、数据规约、数据清理统称为数据预处理。
数据挖掘的技术可粗略划分为:统计分析方法、机器学习方法、神经网络方法和数据库方法。而数据挖掘的主要任务可划分为:建模预测、关联分析、聚类分析、异常检测等。建模预测用于训练模型来预测事务,使其无限接近真实值,其可以用于预测天气情况,病人的患病情况,以及交通状况;关联分析用来发掘出潜藏在事务数据中的关联规则,从而提取有用的模式,它可以用于分析客户的购买行为,个性化推荐等;聚类分析用来找出数据中的群组,使得同一群组中的数据具有极大相似属性,聚类分析可以用于保险公司对客户群体进行分组,对生物基因进行功能分类等;异常检测用来识别数据中特征属性明显不同于其他数据的异常数据,它可以用来检测网络攻击,识别诈骗行为等。
目前,数据挖掘技术已趋于成熟,并应用于商业、金融、医疗、互联网、制造业等诸多领域,并取得丰硕的成果。
2.2 频繁项集
通常把含有0个或多个项的集合叫作项集,若项集中有N个项,那么它就是N项集。
候选项集:用来获得频繁项集的候选项,它是I中一个或多个项的组合,若包含N个项就成为候选N项集。从候选项集中挑出大于等于min_support的项集,则产生了频繁N项集。
支持度计数:是指项集在总的数据集合中出现的频度,该值对筛选频繁模式和强关联模式起至关重要的作用。
频繁项集:是指总的事务数据集合中频繁出现的项的集合,一般情况,当项集出现的频率满足某一参数时就可以认为它是频繁的,这一参数叫做最小支持度,不满足这一参数的项集叫做非频繁项集。根据以上定义可以得出两个重要定理:
-
如果一个项集是频繁的,那么它的所有子集也都是频繁的。
-
如果一个项集是非频繁的,那么它的所有父集都是非频繁的。
2.3 关联规则
关联规则描述的是事务间的联系,若它们有因果关系或者某种特殊规律,我们就称它为关联。设A,B两个集合没有交集,分别代表不同事件,那么称表达式A→B为关联规则。频繁项集挖掘的目的就是发掘出隐藏在数据库中的关联信息,例如超市或电商根据关联分析得出消费者购买某些商品的同时还可能购买哪些商品,或者计算购买某些商品的同时购买另一些商品的概率有多大。
关联规则的产生是基于对历史数据的概率统计而得出的,所以我们需要用一个度量单位来衡量该规则的强度,它就是置信度。置信度用来权衡规则是否可信,支持度主要反映该规则在整个数据集中的权重。
关联规则可以用条件概率来表示,例如规则A→B的支持度可表示为:
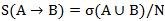
N表示数据集中的总项数。
置信度可表示为:

同时满足min_support和min_confidence的规则称为有趣规则,一般min_support和min_confidence的取值有相关领域的专家来指定。支持度较低的规则一般都具有较高的偶然性,最小支持度阈值用来过滤掉那些没有意义的规则。最小置信度用来挑选出有趣的关联规则,置信度越高,该规则对生产实践就越具有指导意义。发掘事务集中的频繁模式可分成以下两个步骤:
-
从候选集中剔除小于min_support的项,留下的就是频繁集。
-
对频繁集的所有非空子集进行排列组合,构成不同的规则,根据min_confidence阈值,筛选出强关联规则。
通常挖掘频繁项集所耗费的时间远大于计算关联规则所用时间,所以,频繁项集挖掘算法的效率取决于挖掘频繁项集的效率。
2.4 开发工具及语言
本次毕业设计的编码工具采用的是一个轻量、简洁、高效、跨平台的编辑器SublimeText3,它同时支持Windows/Linux/Mac等操作系统,无需安装,解压即可使用。SublimeText3支持语法高亮、自动补全、配色等诸多功能,为开发者提供了一个舒适美观的开发环境。它还有良好的扩展功能,只需要安装Package包即可。SublimeText3所支持的语言也特别丰富,不如主流的C,C++,C#,CSS,HTML,Java,JavaScript,MATLAB,PHP,Python,R,SQL,XML等等,对于这些语言都支持自动补全功能,非常智能。本次毕业设计使用SublimeText3编写Python代码,目前编写Python代码的开发工具有很多,比如Vim,Eclipse,PyCharm,NotePad++等等,他们都有一个共同的缺点就是重量级,启动速度慢,没有SublimeText3方便快捷。
Python是一个同时具有解释性、编译性、互动性和面向对象的脚本语言。Python语言语法简单,易于学习,是很多初学者的入门语言。尽管它语法简单,但是它可以实现非常复杂的程序。Python提供了非常完善的内置代码库,覆盖了网络、文件、GUI、数据库等方面,开发过程中,我们不用亲自实现那些功能,只需要调用库函数即可。除了内置库,Python还支持第三方库,别人开发好的用例经过封装之后就可以直接嵌入到自己的代码中使用,同时自己的代码也可以打包封装与别人共享。Python还具有良好的扩展性和嵌入性,我们能把其他语言编写的代码在Python程序中使用,也能将Python代码嵌入到其他语言为其提供脚本服务。Python还支持面向对象编程,与其他面向对象语言相比,Python以一种简单而又强大的方式实现面向对象编程。目前Python的主要应用领域有:云计算、Web开发、人工智能、系统运维以及图形GUI等,尤其是近两年人工智能与机器学习成为热门领域,Python也被越来越多的人使用。目前Python有2.X和3.X两个版本,两者语法上有小小的区别,Python3.X支持了2.X不支持的库,但是大多数Python库是同时支持的。
本次毕业设计采用Python内置的标准库Tkinter编写简单的交互界面。Tkinter可以非常便捷地编写GUI界面,不用安装任何插件,只需要在代码中导入Tkinter库,Python默认编辑器IDLE也是使用Tkinter实现的。
2.5 数据准备及预处理
通常在数据挖掘的完整流程中,数据准备和预处理可能占到六七成的时间,主要针对缺失和异常的数据,以及不同的数据格式。针对数据缺失,通常采用元组删除、数据补齐等方法处理,元组删除是指删除不完整的数据单元,从而使数据集具有完整的信息格式。这种方法并不是最佳的解决策略,它是以牺牲原始数据为代价的,被舍弃的信息严重影响到数据的客观性和挖掘结果的完整性;数据补齐是指用特定的值补充遗漏的信息,通常有均值填补法,特殊值填补法和人工填补法,倘若遗漏的信息是数值类型,则从其余数据中抽取对应元素的值,计算出平均值补到缺失的位置;若是非数值类型,则使用众数原理,将出现最多的值填补进去;特数值法是指将缺失的信息当做一个特殊的值看待,但是通常得到的结果偏离了实际;人工填补法是指让了解该数据的人手动填补该数据,这样得到的数据集偏离程度最小,效果也是最好的,但是当数据规模较大的时候,该方法的效率大大降低。异常数据同样可以使用办方法来纠正。
本次毕业设计主要是针对电商及超市等销售行业进行研究讨论,所以数据采用的是某超市一个月的销售订单数据,数据来源于CSDN博客用户分享的Kaggle竞赛公开数据集,数据集中包括销售订单表(order_id,product_id),商品信息表(product_id,product_name,aisle_id,department_id),商品分类表(aisle_id,aisle_name),共计十万多条销售订单。因为是竞赛公开的数据集,所以完备性较高,数据格式是统一的CSV文件格式进行保存的,其数据表的属性比较少,所以在数据处理阶段对于缺少信息的数据直接进行删除。因为订单数据、商品信息和分类信息存储在不同的表中于是在预处理阶段,使用Python将三张表中的信息进行了合并,构成了新的数据表products_aisle(product_id,aisle_id)用于发掘订单数据中商品类别之间的联系。
第三章 算法实现
3.1 Apriori算法
3.1.1 Apriori算法简介
Apriori算法是最经典的频繁项集挖掘算法,其目的是挖掘数据集中项与项之间的关系,整个工作流程由两个阶段构成,首先是发掘出频繁模式,然后由频繁项计算关联规则。该算法的核心内容就是找出数据集中的频繁模式,整个算法过程中该步骤占大部分时间,所以该算法的效率由挖掘频繁项集的效率所决定的,衡量该算法的优劣就看第一个步骤是否高效。
Apriori算法由两个重要定律,也是该算法的核心思想:
-
一个频繁项集所包含的子集都是频繁项集。我们假设有频繁项集{I1,I2,I3},支持度为S,最小支持度为min_support,由于它是频繁的所以S>=min_support,因为I1、I2、I3同时出现的概率大于等于min_support,并且他们自由组合形成的子集出现的频率大于等于S,所以,一个频繁项集所包含的子集也频繁的。
-
若一个项集不是频繁项集,那么它的的父集也一定不是频繁的。我们假设项集{I1}是非频繁项集,所以整个数据集中I1出现的频率小于min_support,所以任何包含I1的项集比如{I1、I2、I3}等出现的频率也都小于min_support,所以他们都不是频繁项集。
有了以上两个重要思想,我们就可以扫描数据集判断哪些项集是频繁的,首先先判断一项集,筛选出频繁一项集后进行随机地两两组合,构成候选的二项集,然后继续使用该思想筛选出频繁二项集,往复迭代下去,直至不能组合出新的候选项集为止,至此所有的频繁项集均已产生,需要特别强调的是,在相同的数据集下,min_support的值不同所产生的频繁项集也是不同的。
3.1.2 Apriori]算法原理
Apriori算法使用广度优先的方法,从候选项集中筛选频繁项,再有频繁项集自我连接产生候选项,如此迭代下去就挖掘出了所有的频繁项集,总结该过程可以分为连接和剪枝两个步骤,以下是具体过程:
假设有表3.1所示的初始数据集。
| TId | Items |
|---|---|
| 01 | L1,L2,L5 |
| 02 | L2,L4 |
| 03 | L2,L3 |
| 04 | L1,L2,L3,L4,L5,L6,L7 |
| 05 | L1,L2,L4 |
| 06 | L1,L3 |
| 07 | L2,L3 |
| 08 | L1,L3 |
| 09 | L1,L2,L3,L4,L5 |
| 10 | L1,L2,L3,L4 |
设min_support=3,min_confidence=0.7,这两个参数是频繁项集挖掘算法中最重要的两个参数,实际应用中可以进行适当的调整以适应算法。首次遍历数据集,计算出每项的支持度,生成候选项集C1,如表3.2所示。
| Item | Support |
|---|---|
| L1 | 7 |
| L2 | 8 |
| L3 | 7 |
| L4 | 5 |
| L5 | 3 |
| L6 | 1 |
| L7 | 1 |
然后根据C1表筛选出支持度计数大于min_support的项,因为{L6},{L7}的支持度计数小于3,故将这两项从候选项集中剔除,其余的项构成频繁一项集L1,结果如表3.3所示。
| Item | Support |
|---|---|
| L1 | 7 |
| L2 | 8 |
| L3 | 7 |
| L4 | 5 |
| L5 | 3 |
接下来的过程是利用L1进行迭代,迭代步骤分为:
连接:将频繁N-1项集每两个进行连接,生成候选N项集。在连接之前我们可以添加条件进行可行性判断,两个频集的前N-2个项是否相同;然后把其余项加在一起共同构成K项集,对所有的频繁K-1项集执行此过程就会得到所有的候选K项集Lk。
剪枝:倘若候选N项集中某一项的支持度小于min_support,则剔除此项;若候选项集中某一项含有非平凡项的子集,根据apriori定律此项也不满足频繁项集条件,也将其删掉,剩余的项构成了频繁K项集Ck。
由L1生成C2如表3.4所示。
| Item | Support |
|---|---|
| {L1,L2} | 5 |
| {L1,L3} | 5 |
| {L1,L4} | 4 |
| {L1,L5} | 3 |
| {L2,L3} | 5 |
| {L2,L4} | 5 |
| {L2,L5} | 3 |
| {L3,L4} | 3 |
| {L3,L5} | 2 |
| {L4,L5} | 2 |
从上表中剔除不满足min_support的项,得到频繁二项集L2,如表3.5所示。
| Item | Support |
|---|---|
| {L1,L2} | 5 |
| {L1,L3} | 5 |
| {L1,L4} | 4 |
| {L1,L5} | 3 |
| {L2,L3} | 5 |
| {L2,L4} | 5 |
| {L2,L5} | 3 |
| {L3,L4} | 3 |
对L2再进行连接步骤,得到候选三项集C3,如表3.6所示。
| Item | Support |
|---|---|
| {L1,L2,L3} | 3 |
| {L1,L2,L4} | 3 |
| {L1,L2,L5} | 3 |
| {L1,L3,L4} | 3 |
| {L1,L3,L5} | 2 |
| {L1,L4,L5} | 2 |
| {L2,L3,L4} | 3 |
| {L2,L3,L5} | 2 |
| {L2,L4,L5} | 2 |
根据min_support对C3进行筛选,得到三项频繁集L3,如表3.7所示。
| Item | Support |
|---|---|
| {L1,L2,L3} | 3 |
| {L1,L2,L4} | 3 |
| {L1,L2,L5} | 3 |
| {L1,L3,L4} | 3 |
| {L2,L3,L4} | 3 |
重复以上步骤,当不能再连接出频繁项集时结束。总的频繁项集如表3.8所示。
| Item | Support |
|---|---|
| {L1} | 7 |
| {L2} | 8 |
| {L3} | 7 |
| {L4} | 5 |
| {L5} | 3 |
| {L1,L2} | 5 |
| {L1,L3} | 5 |
| {L1,L4} | 4 |
| {L1,L5} | 3 |
| {L2,L3} | 5 |
| {L2,L4} | 5 |
| {L2,L5} | 3 |
| {L3,L4} | 3 |
| {L1,L2,L3} | 3 |
| {L1,L2,L4} | 3 |
| {L1,L2,L5} | 3 |
| {L1,L3,L4} | 3 |
| {L2,L3,L4} | 3 |
| {L1,L2,L3,L4} | 3 |
3.1.3 Apriori算法优缺点
Apriori算法最大的特点就是原理简单、易于理解,它使用逐层搜索的方法,利用Apriori的两大定律不断地迭代执行连接和剪枝步骤,大大压缩了数据集,省略了许多不必要的步骤,使得算法更加高效。而且的扩展性比价好,可应用于并行计算等领域。
Apriori的缺点也是决定该算法效率的两大重要因素,一是他要不断地扫描事务数据库,高频率的IO操作大大降低了算法的执行速率;二是在算法迭代时,生成了许多候选集,比如频繁一项集有1000个,那么执行连接步骤后得到的候选二项集可能会有上百万条,严重影响了算法效率。
3.2 Fp-growth算法
3.2.1 Fp-growth算法简介
Fp-growth算法是继Apriori算法之后的另一频繁模式算法,运用深度优先的递归策略。由于Apriori算法需要不断地遍历数据,而且生成大量地候选项,在大数据量的计算中很耗费时间,面对Apriori的缺陷,Fp-growth算法诞生了,该算法可以看做对Apriori算法的优化策略,将数据集存储在树形结构中,命名为Fp-tree,因为Fp-tree存储在内存中,所以在之后的计算中不用再进行IO操作,并且这种方法不会产生候选项,直接从树形结构中得到频繁项集,算法效率有了显著提高。
Fp-growth算法包含两个部分:
- 构建Fp-tree:首次遍历数据集,统计每个元素的支持度计数min_support,剔除掉支持度小于min_support的非频繁项,对余下的频繁项根据min_support由大到小排序得到项头表;再次遍历数据集,把每一条数据参考项头表中的次序添加到Fp树上。
- 挖掘频繁模式:构造好Fp-tree后,就可以通过这棵树发掘出全部频繁项集。首先从项头表排在最后的节点开始,在Fp-tree中自底向上,找出该节点的所有前缀路径,构成该节点的条件模式基,通过条件模式基构造条件Fp-tree,对该树中的节点进行全排列组合,就可以得到频繁项集。重复地迭代这两个步骤,到Fp树中只剩下一个叶节点时结束。
由于Fp-growth算法是直接从Fp-tree上挖掘频繁项,不用像Apriori算法那样不断地自我连接生成大量地候选项,也不用多次遍历数据集,所以它的效率远远大于Apriori算法。
3.2.2 Fp-growth算法原理
Fp-growth算法可以总结为两个核心步骤:构造Fp树和根据Fp树发掘频繁模式。它采用树状结构将数据压缩存储在内存里,然后自底向上进行挖掘。这里我们同样使用Apriori中的演示数据进行Fp-growth算法过程的分析,并且令min_support=3,min_config=0.7。
初始数据集如表3.9所示。
| TId | Items |
|---|---|
| 01 | L1,L2,L5 |
| 02 | L2,L4 |
| 03 | L2,L3 |
| 04 | L1,L2,L3,L4,L5,L6,L7 |
| 05 | L1,L2,L4 |
| 06 | L1,L3 |
| 07 | L2,L3 |
| 08 | L1,L3 |
| 09 | L1,L2,L3,L4,L5 |
| 10 | L1,L2,L3,L4 |
首先进行数据集的第一次遍历,统计各元素的支持度计数,删掉支持度比min_support小的项,剩下的就是频繁一项集,将频繁一项集根据其支持度计数进行降序排序构成项头表,如表3.10和表3.11所示。
| L1 | L2 | L3 | L4 | L5 | L6 | L7 |
|---|---|---|---|---|---|---|
| 7 | 8 | 7 | 5 | 3 | 1 | 1 |
| L2 | L1 | L3 | L4 | L5 |
|---|---|---|---|---|
| 8 | 7 | 7 | 5 | 3 |
| Null | Null | Null | Null | Null |
接下来将数据集中支持度小于min_support的元素删除,并将每一项的元素按照项头表中的顺进行序排,得到表3.12所示。
| TId | Items |
|---|---|
| 01 | L2,L1,L5 |
| 02 | L2,L4 |
| 03 | L2,L3 |
| 04 | L2,L1,L3,L4,L5 |
| 05 | L2,L1,L4 |
| 06 | L1,L3 |
| 07 | L2,L3 |
| 08 | L1,L3 |
| 09 | L2,L1,L3,L4,L5 |
| 10 | L2,L1,L3,L4 |
使用此表和项头表进行Fp树的构造。树中节点的结构为{元素:频度计数 },首先,置Fp-tree的根节点为null,然后将更新后的数据集逐条的插入树中,按照支持度顺序从根节点向下插入,如果待添加的顺序与树中的路径相同,则只需更新对应元素的计数,直至分叉节点,创建新的节点存储分叉节点信息。
向Fp-tree插入第一条数据{ L2,L1,L5 },如图3.1所示。

向Fp-tree插入第二条数据{ L2,L4 },如图3.2所示。

重复此过程,直至最后一条数据{L2,L1,L4,L3}插入到Fp-tree中,如图3.3所示。
至此Fp-tree创建完成,观察这棵树我们可以发现,元素在树中的位置不止一处,这是因为他们具有不同的前缀路径,在某一节点进行分叉。但是我们还是能观察到有很多的相同路径被合并,类似于哈夫曼树,出现频度高的节点靠近根节点,频度低的节点靠近叶子节点,这就实现了数据的压缩存储,使得相同路径上的节点共用内存,即降低了内存压力,也提高了算法效率,这就是在创建Fp-tree时使用降序的原因。到这里Fp-growth算法的第一个核心步骤执行完毕,接下来执行第二个步骤:从这棵树里挖掘出频繁项集。

从fp树中发掘频发模式需要按照项头表里元素的顺序,按照支持度由低到高的顺序进行。首先挖掘L5,由Fp-tree可以看出,从根节点到L5的路径有两条,分别是:

由这两条路径就可以得到L5的条件模式基,记为{L2,L1:1},{L2,L1,L3,L4:2},接下来根据条件模式基,我们可以像构造Fp-tree那样构造出该元素的条件Fp-tree,如图3.4所示。
将该树中支持度小于min_support的节点删除,该条件Fp-tree就可以化简为:{L2,L1:3},接下来根据条件Fp-tree产生频繁项集,首先将条件Fp树每条分支上的节点进行全排列组合,然后与自身节点连接就可得到频繁项集:{L2,L5:3},{L1,L5:3},{L2,L1,L5:3},{L5:3}
接下来该挖掘L4的频繁项集了,过程与上一步完全相同,先找出L4的全部前缀:
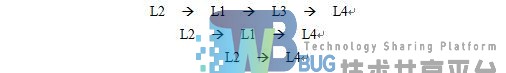
从路径中删除自身节点L4的到L4的条件模式基:{L2,L1,L3:3}
由条件模式基构建条件Fp-tree,如3.5所示。
根据该数可产生频繁模式:{L2,L4:5},{L1,L4:4},{L3,L4:3},{L2,L1,L4:3},{L2,L3,L4:3},{L1,L3,L4:3},{L2,L1,L3,L4:3}

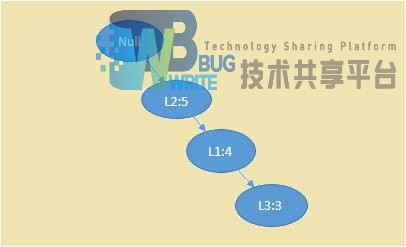
迭代执行上述步骤,直到Fp树中只剩下一个元素为止,所有的频繁项集都产生了,如表3.13所示。
| Frequent_item | Support |
|---|---|
| {L5} | 3 |
| {L2,L5} | 3 |
| {L1,L5} | 3 |
| {L2,L1,L5} | 3 |
| {L4} | 5 |
| {L2,L4} | 5 |
| {L1,L4} | 4 |
| {L3,L4} | 3 |
| {L2,L1,L4} | 3 |
| {L2,L3,L4} | 3 |
| {L1,L3,L4} | 3 |
| {L2,L1,L3,L4} | 3 |
| {L3} | 7 |
| {L2,L3} | 5 |
| {L1,L3} | 5 |
| {L2,L1,L3} | 3 |
| {L1} | 7 |
| {L2,L1} | 5 |
| {L2} | 8 |
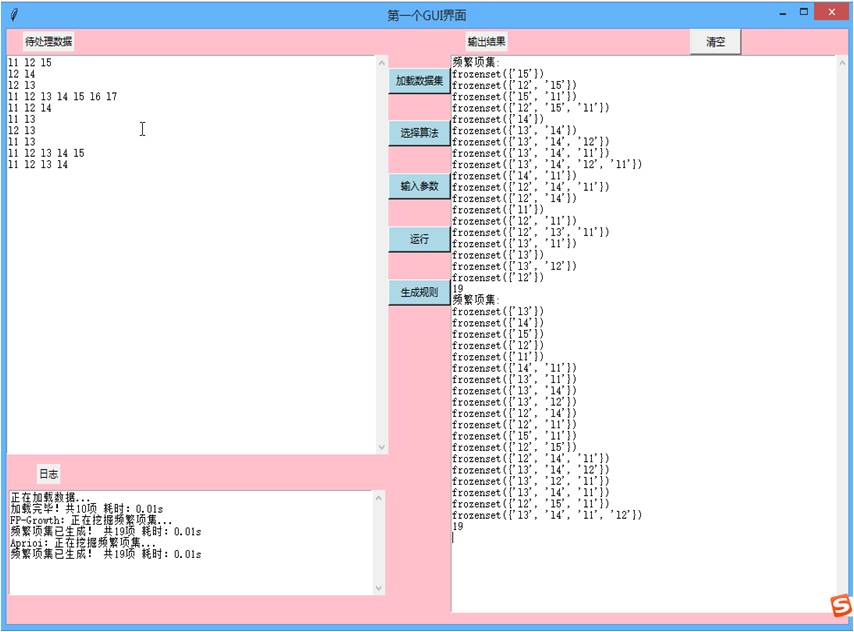
通过观察我们发现,在同一数据集上,采用同样的的最小支持度和最小置信度,Apriori算法和Fp-growth算法挖掘出来的结果是相同的,算法运行结果如图3.6所示。
3.2.3 Fp-growth算法优缺点
Fp-growth算法最大的优点就是它执行速率快,而且要比Apriori算法快一个数量级。整个算法过程只需要扫描两次数据库,可以不用产生候选项集而直接生成频繁项集,这样就节约了很大的内存资源,降低了空间复杂度。在创建Fp-tree的时候,采用了哈夫曼原理,大大压缩了存储空间。
但是Fp-growth算法并不是对所有的数据集上都能取得良好的效果,比如在一个稀疏的数据集上执行此算法,由于数据之间的交集很小,可以合并的元素少,创建的Fp-tree包含特别多的子孙节点,显得特别臃肿,将这样的树保存在内存中丝毫没有起到压缩效果,反而影响到了算法的效率。而且该算法在构造条件Fp树和条件模式基时使用了递归策略,空间复杂度相对较高,内存开销大。
第四章 挖掘关联规则
4.1 计算关联规则
Fp-growth算法和Apriori算法都是频繁模式算法,是整个挖掘过程的第一步,也是最耗时的一步。接下来就是发掘关联规则,其过程分为两步:
- 对任意一个频繁项集,分别列举出他们的非空子集
- 对任意一个子集S,都可产生类似S=>L-S格式的关联,并计算出support和confidence的值。
关联规则支持度的计算方法为:
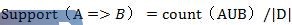
置信度计算方法为:
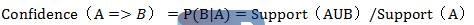
因为关联规则描述的是频繁项集的子集和该子集对应补集之间的联系,所以计算关联规则应该从频繁二项集开始计算。
对于频繁项集{L1,L2,L3,L4},它的所有子集为:{L1},{L2},{L3},{L4},{L1,L2},{L1,L3},{L1,L4},{L2,L3},{L2,L4},{L3,L4},{L1,L2,L3},{L1,L2,L4},{L2,L3,L4},{L1,L3,L4}。对于这些子集所产生的关联规则和规则的置信度如表4.1所示。
| Rules | Confidence |
|---|---|
| {L1}--> {L2,L3,L4} | 0.429 |
| {L2}-->{L1,L3,L4} | 0.375 |
| {L3}--> {L1,L2,L4} | 0.429 |
| {L4}-->{L1,L2,L3} | 0.6 |
| {L1,L2}-->{L3,L4} | 0.6 |
| {L1,L3}-->{L2,L4} | 0.6 |
| {L1,L4}-->{L2,L3} | 0.75 |
| {L2,L3}-->{L1,L4} | 0.6 |
| {L2,L4}-->{L1,L3} | 0.6 |
| {L3,L4}-->{L1,L2} | 1.0 |
| {L1,L2,L3}-->{L4} | 1.0 |
| {L1,L2,L4}-->{L3} | 1.0 |
| {L1,L3,L4}-->{L2} | 1.0 |
| {L2,L3,L4}-->{L1} | 1.0 |
观察表可以发现,这些关联规则的置信度参差不齐,关联规则挖掘的目的就是发现那些置信度高的规则,所以我们需要根据最小置信度min_support阈值来筛选置信度,将那些置信度低的规则舍弃,可得表4.2。
| Rules | Confidence |
|---|---|
| {L1,L4}-->{L2,L3} | 0.75 |
| {L3,L4}-->{L1,L2} | 1.0 |
| {L1,L2,L3}-->{L4} | 1.0 |
| {L1,L2,L4}-->{L3} | 1.0 |
对其他频繁项集同样做相同的操作,就可以得到在min_support=0.3,min_config=0.7下的所有关联规则,如表4.3所示。
| Rules | Confidence |
|---|---|
| {L1}-->{L2 } | 0.714 |
| {L1}-->{L3} | 0.714 |
| {L3}-->{L2} | 0.714 |
| {L3}-->{L1} | 0.714 |
| {L4}-->{L1} | 0.8 |
| {L4}-->{L2} | 1.0 |
| {L4}-->{L1,L2} | 0.8 |
| {L5}-->{L1} | 1.0 |
| {L5}-->{L2} | 1.0 |
| {L5}-->{L1,L2} | 1.0 |
| {L1 ,L2 }-->{L4} | 0.8 |
| {L1,L4}-->{L2} | 1.0 |
| {L1,L4}-->{L3} | 0.75 |
| {L1,L4}à{L2,L3} | 0.75 |
| {L1,L5}-->{L2} | 1.0 |
| {L2,L5}-->{L1} | 1.0 |
| {L2,L4}-->{L1} | 0.8 |
| {L3,L4}-->{L1} | 1.0 |
| {L3,L4}-->{L2} | 1.0 |
| {L3,L4}-->{L1,L2} | 1.0 |
| {L1,L2,L3}-->{L4} | 1.0 |
| {L1,L2,L4}-->{L3} | 0.75 |
| {L1,L3,L4}-->{L2} | 1.0 |
| {L2,L3,L4}-->{L1} | 1.0 |
4.2 结果分析
分别采用Apriori算法和Fp-growth算法对本次毕业设计所采用的十多万条购物订单数据进行统计分析,分别使用min_support=0.01,min_confidence=0.1,共得到频繁项集120项,其中频繁一项集105项,频繁二项集15项。共生成强关联规则26项,如图4.1所示。
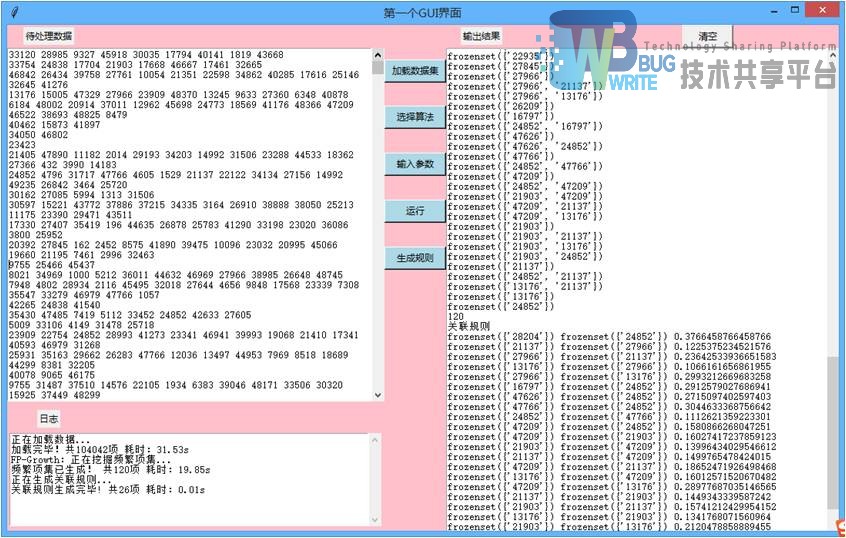
将关联规则中的商品编号和商品信息表products中的进行一一对应,就能看出该超市消费者的消费规律,结果如表4.4所示。
| Rules | Confidence |
|---|---|
| 有机富士苹果-->香蕉 | 0.38 |
| 有机草莓-->有机树莓 | 0.12 |
| 有机树莓-->有机草莓 | 0.24 |
| 有机香蕉袋-->有机树莓 | 0.11 |
| 有机树莓-->有机香蕉袋 | 0.30 |
| 草莓-->香蕉 | 0.29 |
| 大柠檬-->香蕉 | 0.27 |
| 有机鳄梨-->香蕉 | 0.30 |
| 香蕉-->有机鳄梨 | 0.11 |
| 有机哈斯鳄梨-->香蕉 | 0.16 |
| 有机哈斯鳄梨-->有机菠菜 | 0.16 |
| 有机菠菜-->有机哈斯鳄梨 | 0.14 |
| 有机草莓-->有机哈斯鳄梨 | 0.15 |
| 有机哈斯鳄梨-->有机草莓 | 0.19 |
| 有机香蕉袋-->有机哈斯鳄梨 | 0.16 |
| 有机哈斯鳄梨-->有机香蕉袋 | 0.29 |
| 有机草莓-->有机菠菜 | 0.14 |
| 有机菠菜-->有机草莓 | 0.16 |
| 有机香蕉袋-->有机菠菜 | 0.13 |
| 有机菠菜-->有机香蕉袋 | 0.21 |
| 香蕉-->有机菠菜 | 0.11 |
| 有机菠菜-->香蕉 | 0.22 |
| 有机草莓-->香蕉 | 0.22 |
| 香蕉-->有机草莓 | 0.12 |
| 有机草莓-->有机香蕉袋 | 0.23 |
| 有机香蕉袋-->有机草莓 | 0.16 |
观察该表可知,该超市香蕉,草莓,梨,菠菜,柠檬,苹果,树莓之间存在着关联信息。
同样我们用这两种算法对购物订单的商品类别进行分析,记min_support=0.1,min_confidence=0.5;则共生成频繁项集37项,强关联规则27项,结果如表4.5所示。
| Rules | Confidence |
|---|---|
| 酱油-->鲜果 | 0.69 |
| 面包-->鲜果 | 0.69 |
| 椒盐卷饼-->鲜果 | 0.62 |
| 酸奶-->鲜果 | 0.71 |
| 干酪-->蔬菜 | 0.59 |
| 包装蔬菜-->鲜果 | 0.74 |
| 蔬菜-->鲜果 | 0.72 |
| 鲜果-->蔬菜 | 0.57 |
| 苏打水-->鲜果 | 0.58 |
| 干酪-->鲜果 | 0.68 |
| 牛奶-->蔬菜 | 0.51 |
| 牛奶-->鲜果 | 0.68 |
| 酸奶-->蔬菜 | 0.55 |
| 包装蔬菜-->蔬菜 | 0.64 |
| 蔬菜-->包装蔬菜 | 0.53 |
| 酸奶、包装蔬菜-->鲜果 | 0.82 |
| 酸奶、鲜果-->包装蔬菜 | 0.55 |
| 酸奶、蔬菜-->鲜果 | 0.82 |
| 酸奶、鲜果-->蔬菜 | 0.63 |
| 牛奶、蔬菜-->鲜果 | 0.80 |
| 鲜果、牛奶-->蔬菜 | 0.61 |
| 蔬菜包装、蔬菜-->鲜果 | 0.80 |
| 鲜果、包装蔬菜-->蔬菜 | 0.69 |
| 鲜果、蔬菜包装-->蔬菜 | 0.59 |
| 包装蔬菜-->鲜果、蔬菜 | 0.51 |
| 干酪、蔬菜-->鲜果 | 0.78 |
| 干酪、鲜果-->蔬菜 | 0.67 |
由此表可以得出顾客在购买不同商品之间的关联关系,超市或者电商可以以此为根据来调整商品的布局,对用户进行精准推荐,合理的进行商品促销等,实现销量的提升。
4.3 算法对比
Apriori和Fp-growth算法都是关联规则挖掘中的经典算法,Apriori采用广度优先的迭代方法,Fp-growth采用深度优先的递归方法。两者各有利弊,有各自不同的使用情景。
Apriori算法的原理比较简单,就是一层一层地迭代,先生成候选项,然后根据min_support剔除掉非频繁项,得到该层的频繁项集,迭代此过程,这就是apriori算法的核心思想,正是由于它的结构简单,易于理解,才有了良好的发展和广泛的应用。在apriori算法的执行过程中,使用了很多技巧来提高算法的效率,比如剪枝策略,它可以剔除不满足apriori定律的候选项,使得候选项大幅度减少,这是专门针对apriori算法而设计的候选产生方法。而apriori也存在两个严重的缺陷,就是在算法迭代时需要不断地遍历数据集以及生成大量的候选项。每执行一次迭代就需遍历一次,需要挖掘频繁K项集就要遍历K次,当数据集比较大或者需要挖掘的频繁模式较长,则算法的效率大大降低。算法的迭代过程是在内存中进行的,所有的候选项也在内存中存储,当数据量较大时产生的候选项集数据非常巨大,严重影响了算法的适应性和效率。为了降低挖掘过程中的多次I/O,通常针对不同的数据集需要对算法进行适当的优化。
Fp-growth算法的提出大大弥补了Apriori算法的不足,Fp-growth算法思想中同样用到了Apriori定律,可以看做是对Apriori算法改良算法。该算法采用递归策略,将数据集以树形结构存储在内存中,既压缩了数据量,也减少了访问数据库的次数,大幅度提高了算法效率,这也是Fp-growth算法相对于Apriori算法最主要的优点。在创建Fp-tree时,由于许多节点出现的频率较高,于是可以将他们进行合并,这就实现了压缩效果,在挖掘频繁项集也是直接在这棵树上进行,不用再去扫描数据库,而且不会生成大量地候选项集,只得到条件模式基,大大缓解了内存压力。对于一个稠密数据集,使用该算法可以将数据压缩到比原来小很多,使得多条数据共享一个分支。由于只需要遍历两次数据集,大幅度地降低了I/O,算法效率显著提高。但是在稀疏数据集上,Fp-tree的压缩效果不是很明显,这是由于这些数据元素不能在fp树中共用节点,每个不同的元素都需要申请内存存放,当数据量大是该方法不可取。
第五章 总结与展望
5.1 总结
本文先是介绍了频繁项集挖掘的背景和意义,以及应用领域,接着介绍了数据挖掘的以及频繁模式的相关理论。着重介绍了频繁项集挖掘中的两个经典算法Apriori和Fp-growth,详细描述了两个算法产生频繁项集的过程。作为最经典、应用最广泛的数据挖掘算法,频繁项集和关联规则的挖掘一直是人们学习和研究的对象。
以下是本文所做的主要工作:
-
详细阐述了挖掘流程,对每个步骤都进行了简单描述,着重描述了数据预处理阶段,因为在一般的数据挖掘工作中,这一步可能消耗70%的时间。
-
分别使用Python语言实现了Apriori算法和Fp-growth算法,使用这两种算法对同一数据集采用相同的支持度和置信度进行挖掘,校验两者结果的准确性。对比两种算法的效率。
-
挖掘出频繁项集里的强关联规则,对照规则和原始数据对结果进行简单分析,分析用户的购买习惯以及规律。
-
使用Python内置的GUI库Tkinter编写简单的操作界面,使用该界面进行上述操作,实现交互功能。
5.2 展望
目前频繁项集挖掘算法已经被应用到各行各业,并且针对不同的应用领域做了适应性的优化。本文只是简单的针对经典的Apriori算法和Fp-growth算法进行研究和实现,还需要进一步优化算法来解决算法效率问题以及可能遇到的其他问题,主要考虑以下方面:
目前我们处在一个大数据时代,各行各业都积累了海量的数据,传统的Apriori算法没有经过优化无力应对如此庞大的数据集,可以考虑并行化处理,将数据分成很多个部分,分别计算出每个部分的频繁项集,然后将这些项集合在一起挖掘出最终的频繁项集。
由于Apriori算法在挖掘过程中会产生大量地候选项,既影响算法效率又占用内存,在今后的研究中可以考虑用hash函数来映射频繁项集,这样就可以数据集分成很多个部分,对照最小支持度,将小于最小支持度的那一部分删除,就可以减少不必要的操作,不用产生无用的候选项
使用抽样法对研究数据选取一个子集,对这个子集进行频繁项集挖掘,牺牲精确度来换取计算效率
致 谢
时光荏苒,大学四年的学习时光即将进入尾声,特别感谢母校对我的培养教育,为我创造积极地学术氛围和舒适的学习环境,也特别感谢恩师们大学四年对我的谆谆教诲和悉心关怀。
本论文是在老师的的悉心指导和严格要求下完成的,老师学识渊博、治学严谨、平易近人,从选题到中期检查和代码验收,以及论文的反复修改,整个过程都凝聚着老师的汗水和心血。同时也要感谢室友们这一路的陪伴,此次毕业设计中室友们也提供了很多帮助。也感谢本次毕业设计所参考到的书籍文献的给为作者,感谢你们为我铺路,让我汲取到这么多知识。
最后,向百忙之中审阅本论文的各位老师表示由衷的感谢!学海无涯,进无止境,今后我会铭记母校和恩师的教诲,继续保持着一颗积极好学的心,衷心祝愿母校蒸蒸日上,祝各位恩师身体健康。
参考文献
[1] JiaweiHan,MichelineKamber, JianPei,等. 数据挖掘:概念与技术[M].机械工业出版社,2012:146-181.
[2] 刘世平.数据挖掘技术及应用[M].高等教育出版社,2010:64-90.
[3] Kaur P,Attwal KS.Data Mining:Review[J].International Journal of Computer Science & Information Technolo,2014:155-190.
[4] 王爱平,王占凤,陶嗣干,等.数据挖掘中常用关联规则挖掘算法[J].计算机技术与发展,2010, 20(4):105-108.
[5] 郭涛,张代远.基于关联规则数据挖掘Apriori算法的研究与应用[J].计算机技术与发展,2011, 21(6):101-103.
[6] 徐辉增.关联规则数据挖掘方法的研究[J].科学技术与工程,2012, 12(1):60-63.
[7] Lin M Y, Lee P Y, Hsueh S C. Apriori-based frequent itemset mining algorithms on MapReduce[C]//Proceedings of the 6th international conference on ubiquitous information management and communication. ACM, 2012:144-217.
[8] Fernando B, Fromont E, Tuytelaars T. Effective use of frequent itemset mining for image classification[C]//European conference on computer vision. Springer, Berlin, Heidelberg, 2012: 214-227.
[9] 王祥瑞.数据挖掘技术中关联规则挖掘的应用研究[J].煤炭技术,2011, 30(8):205-207.
[10] 李瑞华,鱼斌.基于关联规则的数据挖掘算法研究[J].榆林学院学报,2010, 20(2):62-64.
[11] 刘步中.基于频繁项集挖掘算法的改进与研究[J].计算机应用研究,2012, 29(2):475-477.
参考文献
- 基于数据挖掘技术的企业员工信息系统设计与实现(燕山大学·韩旭)
- 结合时间和评分信息的关联规则推荐系统的研究(南京财经大学·颜文静)
- 频繁项集挖掘算法的研究与应用(南京邮电大学·蒋东洁)
- 面向数据流的近期加权频繁项集挖掘及应用(太原科技大学·贺慧爱)
- 基于J2EE的空间关联规则挖掘理论研究与原型系统实现(福州大学·张群洪)
- 个性化电影推荐系统的研究与实现(华侨大学·朱小琴)
- 基于Web使用挖掘的在线报名推荐系统的研究与实现(电子科技大学·王玥)
- 基于数据挖掘技术的企业员工信息系统设计与实现(燕山大学·韩旭)
- 基于关联规则的网上购物系统的研究与实现(山西财经大学·张栋)
- 基于Apriori算法的网络精准营销系统的设计与实现(河北科技大学·张波)
- 结合时间和评分信息的关联规则推荐系统的研究(南京财经大学·颜文静)
- 基于差分隐私保护的频繁项集挖掘算法研究(西安理工大学·罗沛)
- 旅游推荐系统的研究与设计(浙江理工大学·黄建)
- DM2平台的扩展及其在铁路货票数据上的挖掘应用研究(北京交通大学·王誉泽)
- 基于Hadoop的电商平台用户数据挖掘研究(华北电力大学·王治博)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:毕业设计客栈 ,原文地址:https://m.bishedaima.com/yuanma/35422.html