实验题目：北京地铁计价模型分析及计价系统设计

一．引言

2014年12月28日，北京地铁告别了"两元钱随便坐"的时代，实行了新的计费标准。新的计费标准按照乘坐里程计价。通过对离散数学图论部分的学习，我们通过此次实验调查了北京地铁的计价规则，并通过编程的方式对其进行复现，该计价系统只需要在确定起点和终点的情况下寻求最短路径，花费最少的费用完成路程转换，以达到在实际情况下提高所学知识运用能力的目的。

二．技术总结

1 资料查阅

根据《北京市城市辅导交通车票使用规则》第一章第三条，可知北京地铁按里程计价的规则：

本市轨道交通（除机场线外）实行计程限时票制，具体票价方案为起步6公里（含）内3元，6公里至12公里（含）4元，12公里至22公里（含）5元，22公里至32公里（含）6元，32公里以上部分，每增加1元可乘坐20公里。票价不封顶。乘客乘坐轨道交通一次行程在付费区内最多可停留4小时。

在遇到起点和终点存在多种换乘线路的情况时，应当按照最短换成里程计算票价。

由计价方式可将地铁计价问题抽象为图论中的最短路径问题：[]{#_Hlk531262996 .anchor}将地铁线路图抽象为无向简单赋权图，车站为图中的节点，地铁线路为边，将站间距离作为权值。通过求最短路径的算法即可求得其最短路径。利用最短路径长度通过计价标准计算可得票价。

站间距离可以从北京地铁官网(https://www.bjsubway.com/station/zjgls/）查询得到。

2 设计思路

此次实验的核心为利用迪杰斯特拉算法求出给定起点和终点之间的最短距离从而得出花费最低的票价完成目的。以下进行分析阐述。

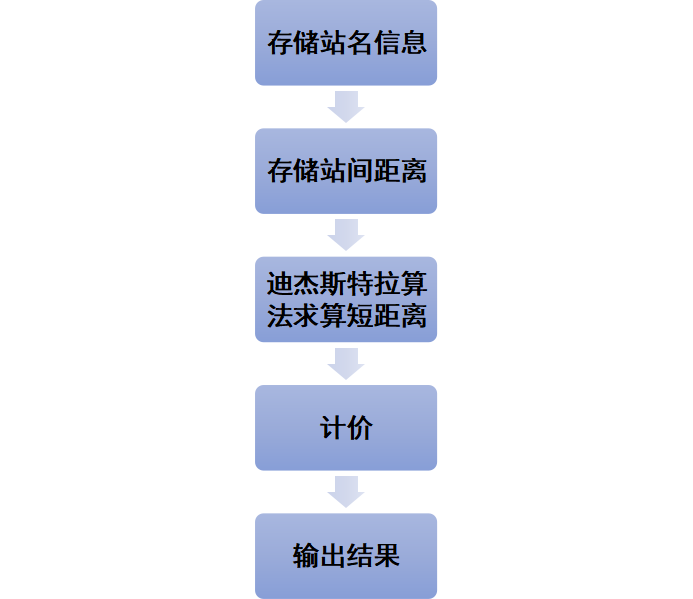
3 问题分析

首先将从北京地铁官网可获取本次实验所需要的1、2、10、13号线地铁线路图如下：

其次，根据所学图论知识，将图中车站画为节点，地铁线路为连结两节点的边，将站间距离作为权值赋权，通过手绘无向简单带权图，建立地铁线路系统分析的模型如下：

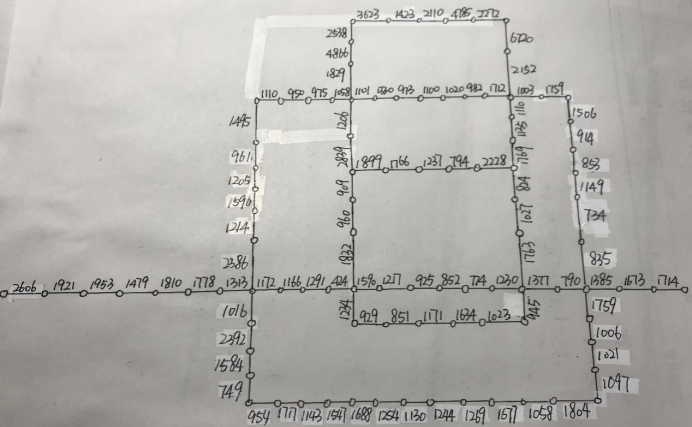
建立初步模型后，接下来就是搭建数据储存的几种机制。得出以下两种方式储存地铁站间距离，一是通过二维数组直接进行所有点间的权重（即距离）的遍历，二是通过一维数组进行相邻站点间的距离的储存，在调用时再新建邻接矩阵进行图的矩阵化。

在邻接矩阵准备完毕后，通过我们此次试验需要用到的核心算法Dijkstra算法进行计算得到最短路径来用于求取费用，最后输出我们想要的结果。

三．系统与算法

1 理论分析Dijkstra算法

Dijkstra算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法。

（1）算法特点：Dijkstra算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树。

（2）算法思想：设G=\<V,E>是一个带权有向图，把图中顶点分成两部分，一部分为最短路径已使用过的点的集合（设为S），另一部分为还未经过的点的集合（设为U），初始时S只有一个源点，按照最短路径长度的递增次序依次把U中的顶点加入到S中，在此过程中总是保持源点到S中顶点的最短路径长度不大于源点到U中任何顶点的最短路径。

每个顶点同时还对应一个距离，S中顶点的距离就是从源点到此顶点的最短路径长度。

（3）算法描述：

（a）初始时，S只包含起点v，U包含除源点v外的其他顶点，U中顶点的距离为源点v到该点的距离\<v,v'>，如果源点v与此顶点不可达，则距离为无穷大；

（b）从U中选出距离最短的顶点k，并将此点加入到S中，同时从U中移除；

（c）更新U中各顶点到源点v的距离（利用k来更新，用源点到U中顶点的距离与源点先到k再到U中顶点的距离进行比较，选择最小值更新源点v到U中各顶点的距离值；

（d）重复（b）（c）步，直到遍历到终点结束，找到源点到终点的最短路径。

在地铁收费系统中，利用Dijkstra算法求出最短路径后与收费标准进行比较，输出最终的票价。

2 计价系统数据处理和计费处理

（1）站名处理：定义一个常量字符串数组用于存放所有地铁站的英文名，据统计，四条线一共有94个不同的站点名，如下图所示：

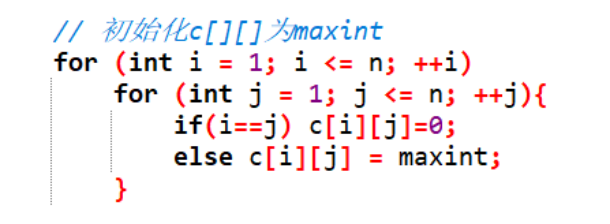
（2）站间距离处理：通过建立二维数组构建邻接矩阵，如下图，先将二维数组中不同点间距离置为无穷大，即maxint，相同点距离置为0，通过手动录入北京地铁官网所有两站的距离，可以发现两点间互通，得到的是无向图，邻接矩阵也是个对称矩阵。二维数组中的索引为1也就是我们一号线的起点"苹果园"的索引，索引为2也就是"古城"，以此类推。c[1][2]也就是存储了这两个索引之间的距离。

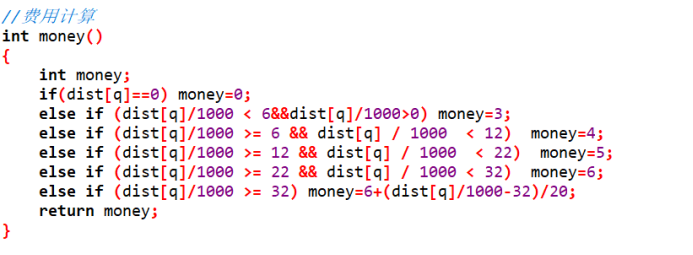
（3）计价处理，也就是将用Dijkstra算法获取的最短路径来用官网的计费公式实现：

3 Dijkstra算法源码展示

c++ void Dijkstra(int v, int \*dist, int \*path, int c\[maxnum\]\[maxnum\]) { bool s\[maxnum\]; // 判断是否已存入该点到S集合中 for (int i = 1; i \<= n; i++) { dist\[i\] = c\[v\]\[i\]; s\[i\] = 0; // 初始都未用过该点 if (dist\[i\] \< maxint) path\[i\] = v; else path\[i\] = 0; } dist\[v\] = 0; s\[v\] = 1; for (int i = 2; i \<= n; i++) { int distance = maxint; int k = v; // 找出当前未使用的点j的dist\[j\]最小值 for (int j = 1; j \<= n; j++) if ((!s\[j\]) && dist\[j\]\<distance) { k = j; // k保存当前邻接点中距离最小的点的号码 distance = dist\[j\]; } s\[k\] = 1; // 表示k点已存入S集合中 for (int j = 1; j \<= n; j++) // 更新dist if ((!s\[j\]) && c\[k\]\[j\]!=maxint) { int newdist = dist\[k\] + c\[k\]\[j\]; if (newdist \< dist\[j\]) { dist\[j\] = newdist; path\[j\] = k; } } } }

4 Dijkstra算法代码分析

（1）根据理论分析的Dijkstra算法的基本原理，为了避免重复返回查找，提高效率，定义了一个用来装已查询过得点的"盒子"，用于判断点是否被找寻连接过。例如：在无向图中A点找寻与其相邻的点B，C，D......紧接着从B点继续向周围找点是就不会再去找寻A点来计算，因为这一步是重复操作，没有必要进行的。在这个函数里我们可以用一个布尔类型的数组用来存放所有地铁站是否被访问过的状态。True即为访问过，False即为没有。

bool s[maxnum]; // 判断是否已存入该点到S集合中

（2）设置的参数v即为输入的站点的起点索引，参数dist数组便是存储当前最小距离，参数path数组存放每次计算的新起点的索引。首先初始化起点到其他各点的距离，并将这些所有点初始化未被访问过。并对找到的能通过联通的下一个点的索引存入path数组里作为下一轮的新起点。

for (int i = 1; i \<= n; i++)

{ dist[i] = c[v][i];

s[i] = 0; // 初始都未用过该点

if (dist[i] \< maxint) path[i] = v;

else path[i] = 0; }

（3）初始化之后，将起点初始最短距离置零,并将起点置为被访问过。

dist[v] = 0; s[v] = 1;

（4）通过循环遍历查找最短路径，distance存放新起点出发的邻近最短距离，定义k表示新的起点，在新的起点查找邻近点并排除访问过的点，找到联通的点并将距离存储在distance变量中，此时找到了下一个新的起点，同时将旧的起点设置为访问过。再次更新dist数组，在找出新的最短路径，也就是从最初我们输入的起点到遍历的最新点的距离的最短距离，也就是通过定义新的变量newdist暂时存储新的距离，与之前到达该点的距离进行比较，取最小的放入dist数组里。反复循环到所有点都访问过后。Dist[i]所存储的数据也就是以起点v到索引为i的地铁站的最短路径的距离了，这时候，我们把i赋值为我们要输入的终点的索引，也就完成了起点到终点的最短距离。

c++ int distance = maxint; int k = v; for (int j = 1; j \<= n; j++) if ((!s\[j\]) && dist\[j\]\<distance) { k = j; distance = dist\[j\]; } s\[k\] = 1; // 表示k点已存入S集合中 for (int j = 1; j \<= n; j++) // 更新dist if ((!s\[j\]) && c\[k\]\[j\]!=maxint) { int newdist = dist\[k\] + c\[k\]\[j\]; if (newdist \< dist\[j\]) { dist\[j\] = newdist; path\[j\] = k; } }

（5）由此可见，迪杰斯特拉算法的"贪心"之处也可见了，我们遍历了起点到所有其他地铁站的最短路径，却只需要用到其中一个最短的路径，也就是终点的路径距离，大部分的其他的都是我们不需要的距离。

5 Dijkstra算法代码模块的不同实现形式

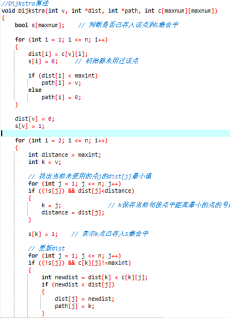
C++实现方案

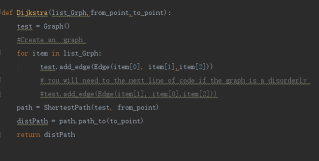
python实现方案

四．实验与测试

对于通过分析解决得到的代码体系，我们选取了三组有代表性的数据进行试验与测试，结果如下图展示：

选取的三组数据：

苹果园到五道口
北京站到草桥
巴沟到前门

图（a1）系统测试结果1

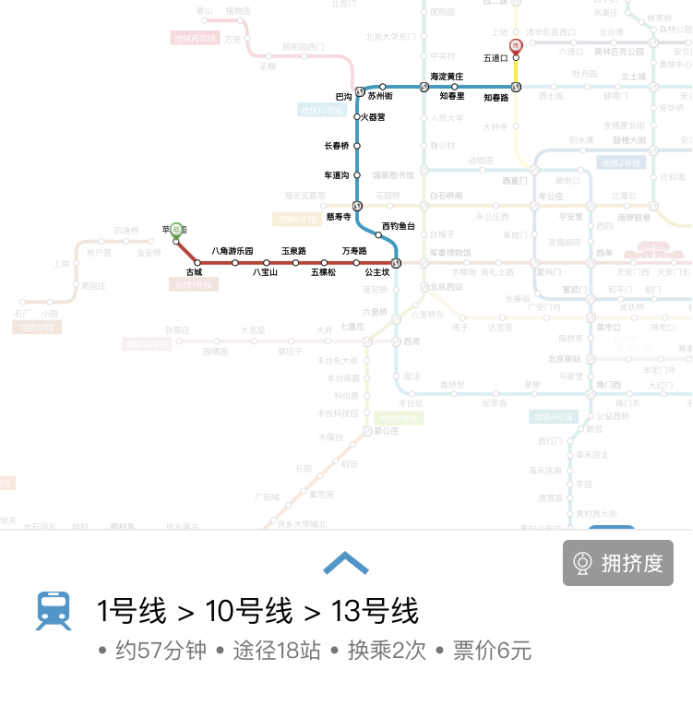
图（a2）北京地铁手机程序官方结果1

图（b1）系统测试结果2

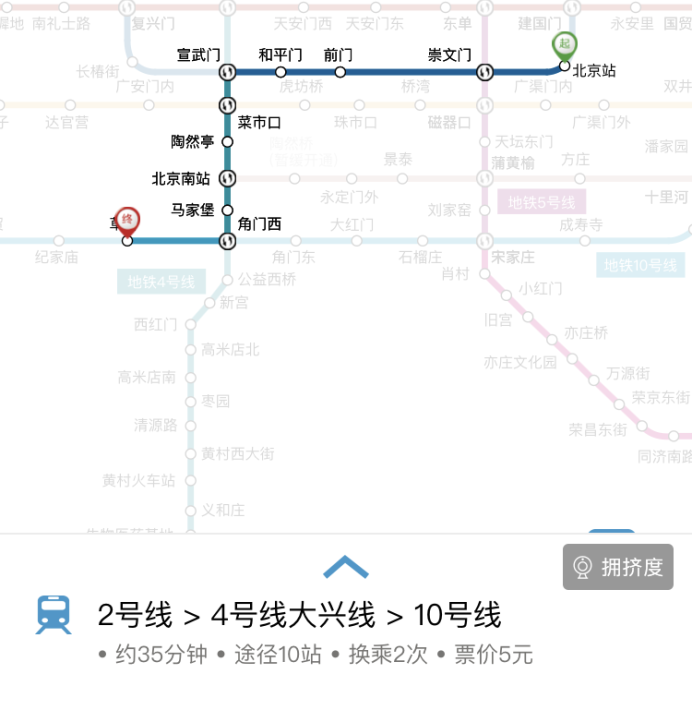
图（b2）北京地铁手机程序官方结果2

图（c1）系统测试结果3

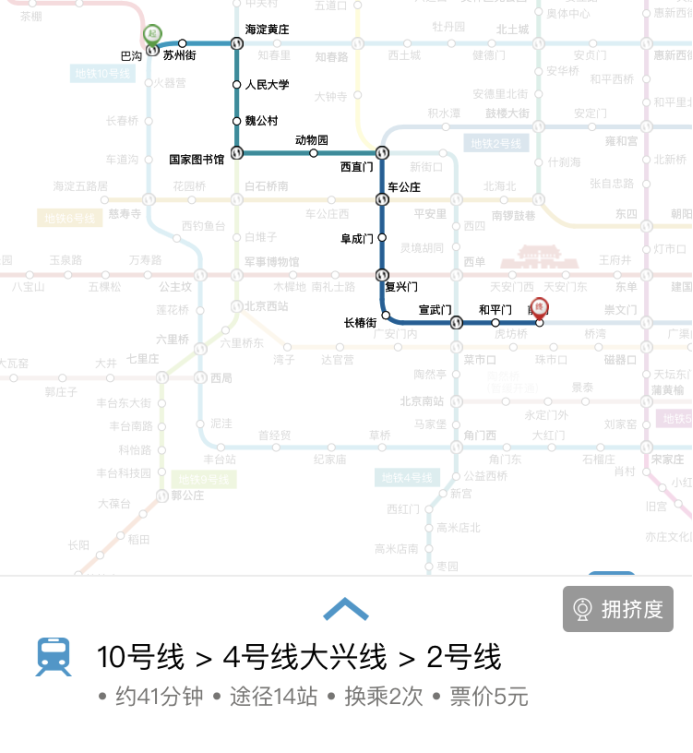
图（c2）北京地铁手机程序官方结果3

由上系列图可见，经过多组测试，实验与实际情况基本相符。

五．总结

地铁收费系统以Dijkstra算法求最短路径为主要算法，以北京市地铁收费标准为依据完成出从出发站到终点站的票价的计算。

在着手开始写代码之前，我们从北京地铁官网，以及实地乘坐地铁时收集相关信息，根据课件以及网上资料分析Dijkstra算法的过程，逐步实现向代码的转化。其中我觉得最大的困难是如何把地铁线路转图存放于矩阵中，并将代表站点名的字符串与站点间距一一对应，再通过查阅资料，询问同学后，用字典存放站点名及站点间对应的距离，解决了这个问题。在讲地铁线路转化成图后便可使用Dijkstra算法实现最短路径的计算，与区间票价比较得到最终票价。完成代码编译也出现了或多或少或大或小的问题，基本通过讨论分析，查阅资料一一解决了所有的问题，最终成功实现了地铁系统。

完成收费系统后，加深了我们对Dijkstra算法的认识，同时也对图论部分的知识有了更深刻的理解和感悟，在大作业的实现过程中，我们从最开始不太清楚离散数学这门课程与计算机或者说与专业的关系到逐渐认识到离散在计算机中的应用，这一过程以及这门课的学习对于我们未来的学习是很有帮助的。在这次实验中利用已学过的知识设计了一个完整的系统，深刻体会到了算法在这其中的作用。算法就像是一个系统的灵魂，它能让一个系统富有生机和活力。以前总觉得算法离我们很遥远，但它却应用在了生活的方方面面。离散数学的课程虽然已经结束，但我相信这门课程里学到的知识会让我受益匪浅。这次我们也发现了自己的问题，对就是代码运用不是很熟悉，很多东西需要不停的查找资料。此次实验锻炼了我们在实际问题中运用所学知识的能力。

除此之外，在田老师的陪伴下度过的八周离散数学的学习，我们都在共同进步。田老师您作为新教师，我们能感受到您对教育的热情以及你想让我们学习到更多的心意，从起初对您上课的意见到最后一节课，我们能感受到你的改变，您在努力，想要把更多的知识教授给我们，您用很形象的例子来给我们解释晦涩难懂的定理，我们更好地理解，收获很多。最后，表达我们对您忠心的感谢。