机器学习算法 Python 实现
目录
- 机器学习算法 Python 实现
- 一、线性回归
- 二、逻辑回归
- 逻辑回归_手写数字识别_OneVsAll
- 三、BP 神经网络
- 四、SVM 支持向量机
- 五、K-Means 聚类算法
- 六、PCA 主成分分析(降维)
- 七、异常检测 Anomaly Detection
一、 线性回归
1、代价函数
-
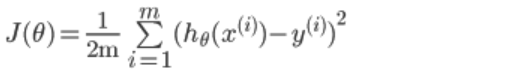
-
其中:
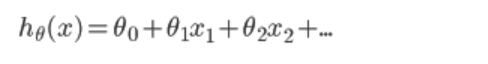
- 下面就是要求出 theta,使代价最小,即代表我们拟合出来的方程距离真实值最近
-
共有 m 条数据,其中
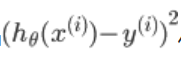 代表我们要拟合出来的方程到真实值距离的平方,平方的原因是因为可能有负值,正负可能会抵消
代表我们要拟合出来的方程到真实值距离的平方,平方的原因是因为可能有负值,正负可能会抵消
-
前面有系数
2的原因是下面求梯度是对每个变量求偏导,2可以消去 - 实现代码:
```
计算代价函数
def computerCost(X,y,theta): m = len(y) J = 0
J = (np.transpose(X*theta-y))*(X*theta-y)/(2*m) #计算代价J
return J
```
- 注意这里的 X 是真实数据前加了一列 1,因为有 theta(0)
2、梯度下降算法
-
代价函数对
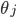 求偏导得到:
求偏导得到:
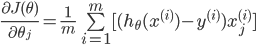
-
所以对 theta 的更新可以写为:
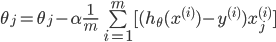
-
其中
 为学习速率,控制梯度下降的速度,一般取
0.01,0.03,0.1,0.3.....
为学习速率,控制梯度下降的速度,一般取
0.01,0.03,0.1,0.3.....
- 为什么梯度下降可以逐步减小代价函数
-
假设函数
f(x) -
泰勒展开:
f(x+△x)=f(x)+f'(x)*△x+o(△x) -
令:
△x=-α*f'(x),即负梯度方向乘以一个很小的步长α -
将
△x代入泰勒展开式中:f(x+x)=f(x)-α*[f'(x)]+o(△x) -
可以看出,
α是取得很小的正数,[f'(x)]也是正数,所以可以得出:f(x+△x)<=f(x) - 所以沿着 负梯度 放下,函数在减小,多维情况一样。
- 实现代码
```
梯度下降算法
def gradientDescent(X,y,theta,alpha,num_iters):
m = len(y)
n = len(theta)
temp = np.matrix(np.zeros((n,num_iters))) # 暂存每次迭代计算的theta,转化为矩阵形式
J_history = np.zeros((num_iters,1)) #记录每次迭代计算的代价值
for i in range(num_iters): # 遍历迭代次数
h = np.dot(X,theta) # 计算内积,matrix可以直接乘
temp[:,i] = theta - ((alpha/m)*(np.dot(np.transpose(X),h-y))) #梯度的计算
theta = temp[:,i]
J_history[i] = computerCost(X,y,theta) #调用计算代价函数
print '.',
return theta,J_history
```
3、均值归一化
- 目的是使数据都缩放到一个范围内,便于使用梯度下降算法
-

-
其中
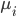 为所有此 feture 数据的平均值
为所有此 feture 数据的平均值
-
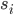 可以是
最大值-最小值
,也可以是这个 feature 对应的数据的
标准差
可以是
最大值-最小值
,也可以是这个 feature 对应的数据的
标准差
- 实现代码:
```
归一化feature
def featureNormaliza(X):
X_norm = np.array(X) #将X转化为numpy数组对象,才可以进行矩阵的运算
#定义所需变量
mu = np.zeros((1,X.shape[1]))
sigma = np.zeros((1,X.shape[1]))
mu = np.mean(X_norm,0) # 求每一列的平均值(0指定为列,1代表行)
sigma = np.std(X_norm,0) # 求每一列的标准差
for i in range(X.shape[1]): # 遍历列
X_norm[:,i] = (X_norm[:,i]-mu[i])/sigma[i] # 归一化
return X_norm,mu,sigma
```
- 注意预测的时候也需要均值归一化数据
4、最终运行结果
-
代价随迭代次数的变化

5、 使用 scikit-learn 库中的线性模型实现
- 导入包
from sklearn import linear_model
from sklearn.preprocessing import StandardScaler #引入缩放的包
- 归一化
# 归一化操作
scaler = StandardScaler()
scaler.fit(X)
x_train = scaler.transform(X)
x_test = scaler.transform(np.array([1650,3]))
- 线性模型拟合
# 线性模型拟合
model = linear_model.LinearRegression()
model.fit(x_train, y)
- 预测
#预测结果
result = model.predict(x_test)
二、 逻辑回归
1、代价函数
-
可以综合起来为:
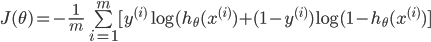 其中:
其中:
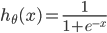
- 为什么不用线性回归的代价函数表示,因为线性回归的代价函数可能是非凸的,对于分类问题,使用梯度下降很难得到最小值,上面的代价函数是凸函数
-
 的图像如下,即
的图像如下,即
y=1时: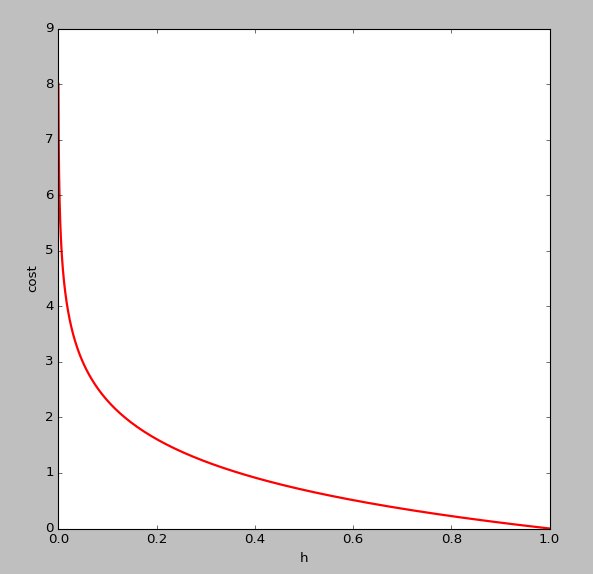
可以看出,当
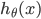 趋于
趋于
1
,
y=1
,与预测值一致,此时付出的代价
cost
趋于
0
,若
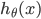 趋于
趋于
0
,
y=1
,此时的代价
cost
值非常大,我们最终的目的是最小化代价值
-
同理
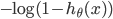 的图像如下(
的图像如下(
y=0):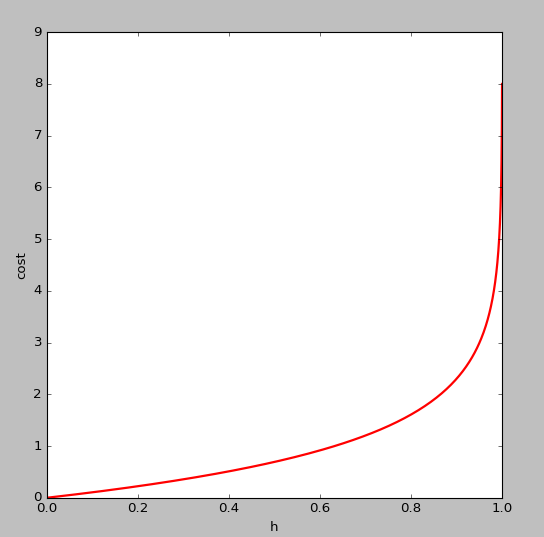
2、梯度
-
同样对代价函数求偏导:
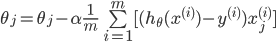 可以看出与线性回归的偏导数一致
可以看出与线性回归的偏导数一致
-
推到过程
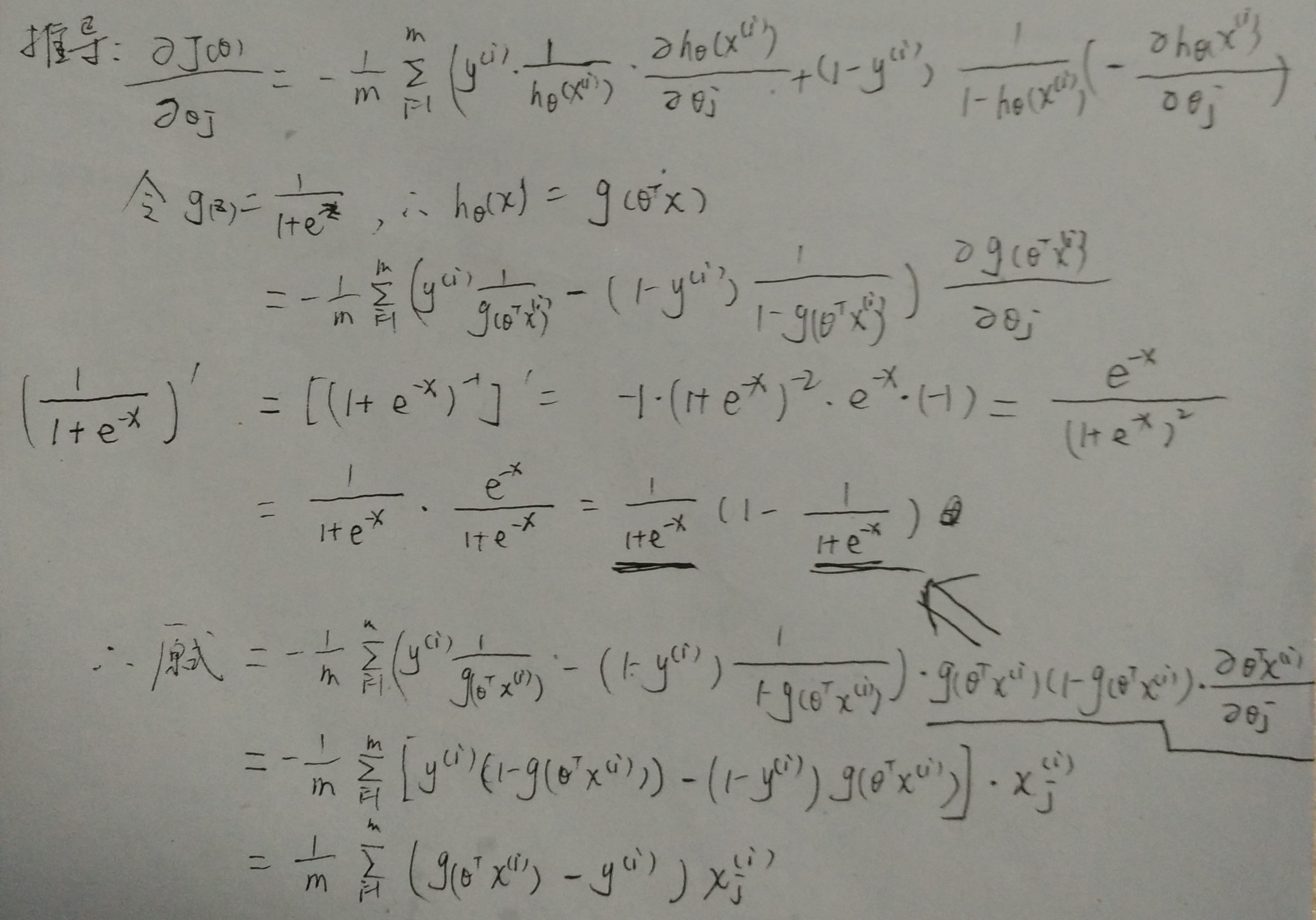
3、正则化
- 目的是为了防止过拟合
-
在代价函数中加上一项
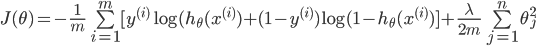
- 注意 j 是重 1 开始的,因为 theta(0)为一个常数项,X 中最前面一列会加上 1 列 1,所以乘积还是 theta(0),feature 没有关系,没有必要正则化
- 正则化后的代价:
```
代价函数
def costFunction(initial_theta,X,y,inital_lambda): m = len(y) J = 0
h = sigmoid(np.dot(X,initial_theta)) # 计算h(z)
theta1 = initial_theta.copy() # 因为正则化j=1从1开始,不包含0,所以复制一份,前theta(0)值为0
theta1[0] = 0
temp = np.dot(np.transpose(theta1),theta1)
J = (-np.dot(np.transpose(y),np.log(h))-np.dot(np.transpose(1-y),np.log(1-h))+temp*inital_lambda/2)/m # 正则化的代价方程
return J
```
- 正则化后的代价的梯度
```
计算梯度
def gradient(initial_theta,X,y,inital_lambda): m = len(y) grad = np.zeros((initial_theta.shape[0]))
h = sigmoid(np.dot(X,initial_theta))# 计算h(z)
theta1 = initial_theta.copy()
theta1[0] = 0
grad = np.dot(np.transpose(X),h-y)/m+inital_lambda/m*theta1 #正则化的梯度
return grad
```
4、S 型函数(即
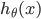 )
)
- 实现代码:
```
S型函数
def sigmoid(z): h = np.zeros((len(z),1)) # 初始化,与z的长度一置
h = 1.0/(1.0+np.exp(-z))
return h
```
5、映射为多项式
- 因为数据的 feture 可能很少,导致偏差大,所以创造出一些 feture 结合
-
eg:映射为 2 次方的形式:
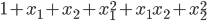
- 实现代码:
```
映射为多项式
def mapFeature(X1,X2): degree = 3; # 映射的最高次方 out = np.ones((X1.shape[0],1)) # 映射后的结果数组(取代X) ''' 这里以degree=2为例,映射为1,x1,x2,x1^2,x1,x2,x2^2 ''' for i in np.arange(1,degree+1): for j in range(i+1): temp = X1 (i-j)*(X2 j) #矩阵直接乘相当于matlab中的点乘.* out = np.hstack((out, temp.reshape(-1,1))) return out ```
6、使用
scipy
的优化方法
-
梯度下降使用
scipy中optimize中的fmin_bfgs函数 - 调用 scipy 中的优化算法 fmin_bfgs(拟牛顿法 Broyden-Fletcher-Goldfarb-Shanno
- costFunction 是自己实现的一个求代价的函数,
- initial_theta 表示初始化的值,
- fprime 指定 costFunction 的梯度
- args 是其余测参数,以元组的形式传入,最后会将最小化 costFunction 的 theta 返回
result = optimize.fmin_bfgs(costFunction, initial_theta, fprime=gradient, args=(X,y,initial_lambda))
7、运行结果
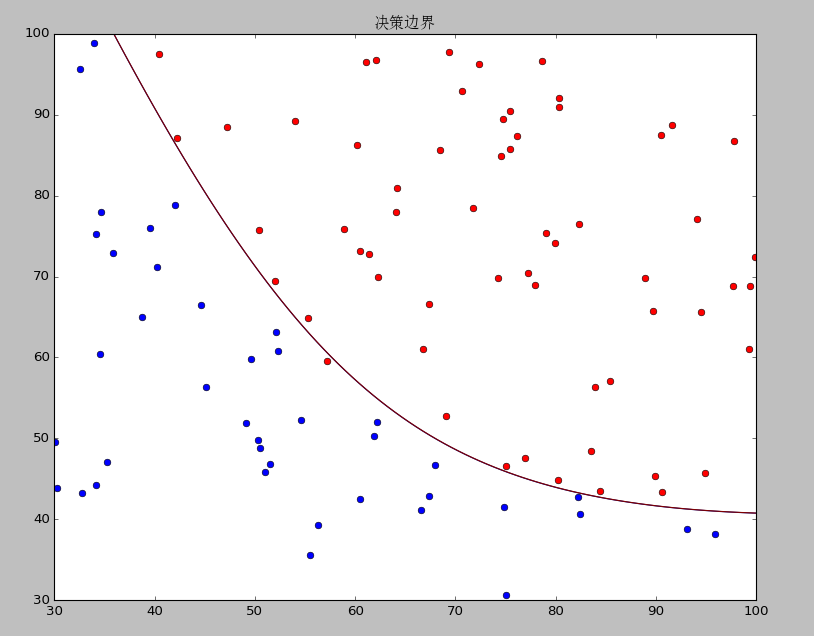
-
data1 决策边界和准确度

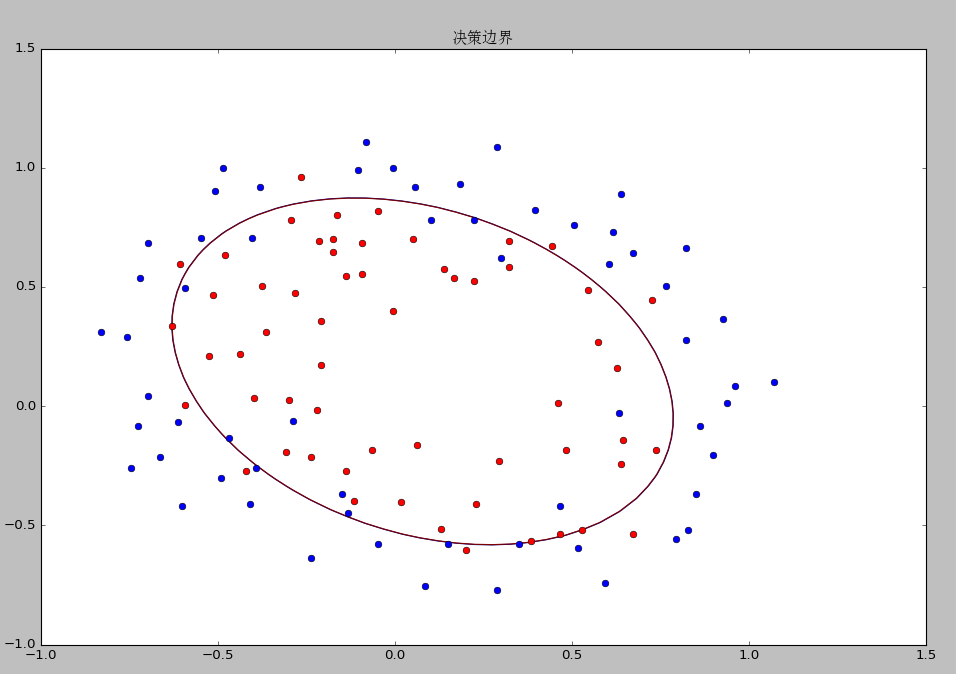
-
data2 决策边界和准确度

8、 使用 scikit-learn 库中的逻辑回归模型实现
- 导入包
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.cross_validation import train_test_split
import numpy as np
- 划分训练集和测试集
# 划分为训练集和测试集
x_train,x_test,y_train,y_test = train_test_split(X,y,test_size=0.2)
- 归一化
# 归一化
scaler = StandardScaler()
scaler.fit(x_train)
x_train = scaler.fit_transform(x_train)
x_test = scaler.fit_transform(x_test)
- 逻辑回归
#逻辑回归
model = LogisticRegression()
model.fit(x_train,y_train)
- 预测
``` # 预测 predict = model.predict(x_test) right = sum(predict == y_test)
predict = np.hstack((predict.reshape(-1,1),y_test.reshape(-1,1))) # 将预测值和真实值放在一块,好观察
print predict
print ('测试集准确率:%f%%'%(right*100.0/predict.shape[0])) #计算在测试集上的准确度
```
逻辑回归_手写数字识别_OneVsAll
1、随机显示 100 个数字
-
我没有使用 scikit-learn 中的数据集,像素是 20*20px,彩色图如下
 灰度图:
灰度图:

- 实现代码:
```
显示100个数字
def display_data(imgData): sum = 0 ''' 显示100个数(若是一个一个绘制将会非常慢,可以将要画的数字整理好,放到一个矩阵中,显示这个矩阵即可) - 初始化一个二维数组 - 将每行的数据调整成图像的矩阵,放进二维数组 - 显示即可 ''' pad = 1 display_array = -np.ones((pad+10 (20+pad),pad+10 (20+pad))) for i in range(10): for j in range(10): display_array[pad+i (20+pad):pad+i (20+pad)+20,pad+j (20+pad):pad+j (20+pad)+20] = (imgData[sum,:].reshape(20,20,order="F")) # order=F指定以列优先,在matlab中是这样的,python中需要指定,默认以行 sum += 1
plt.imshow(display_array,cmap='gray') #显示灰度图像
plt.axis('off')
plt.show()
```
2、OneVsAll
- 如何利用逻辑回归解决多分类的问题,OneVsAll 就是把当前某一类看成一类,其他所有类别看作一类,这样有成了二分类的问题了
-
如下图,把途中的数据分成三类,先把红色的看成一类,把其他的看作另外一类,进行逻辑回归,然后把蓝色的看成一类,其他的再看成一类,以此类推...
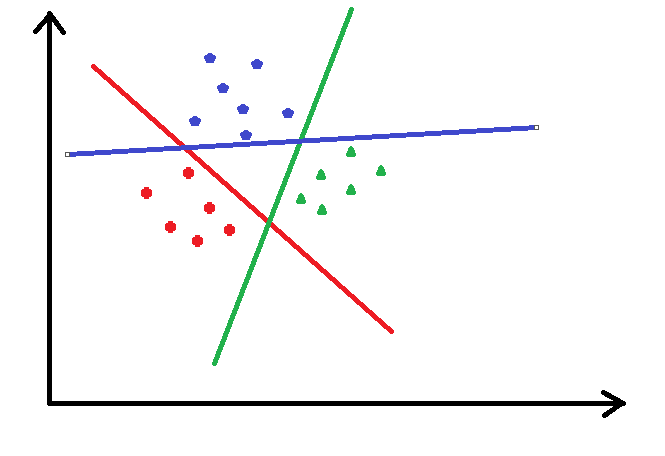
- 可以看出大于 2 类的情况下,有多少类就要进行多少次的逻辑回归分类
3、手写数字识别
- 共有 0-9,10 个数字,需要 10 次分类
-
由于
数据集 y
给出的是
0,1,2...9的数字,而进行逻辑回归需要0/1的 label 标记,所以需要对 y 处理 -
说一下数据集,前
500个是0,500-1000是1,...,所以如下图,处理后的y, 前 500 行的第一列是 1,其余都是 0,500-1000 行第二列是 1,其余都是 0....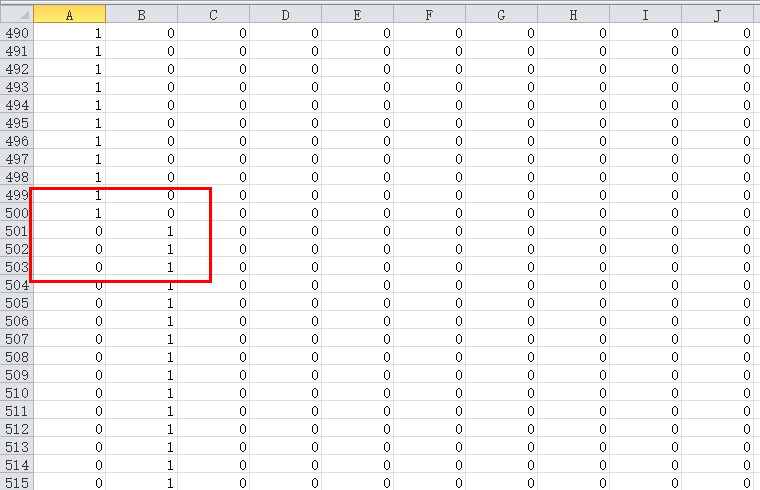
-
然后调用
梯度下降算法
求解
theta - 实现代码:
```
求每个分类的theta,最后返回所有的all_theta
def oneVsAll(X,y,num_labels,Lambda): # 初始化变量 m,n = X.shape all_theta = np.zeros((n+1,num_labels)) # 每一列对应相应分类的theta,共10列 X = np.hstack((np.ones((m,1)),X)) # X前补上一列1的偏置bias class_y = np.zeros((m,num_labels)) # 数据的y对应0-9,需要映射为0/1的关系 initial_theta = np.zeros((n+1,1)) # 初始化一个分类的theta
# 映射y
for i in range(num_labels):
class_y[:,i] = np.int32(y==i).reshape(1,-1) # 注意reshape(1,-1)才可以赋值
#np.savetxt("class_y.csv", class_y[0:600,:], delimiter=',')
'''遍历每个分类,计算对应的theta值'''
for i in range(num_labels):
result = optimize.fmin_bfgs(costFunction, initial_theta, fprime=gradient, args=(X,class_y[:,i],Lambda)) # 调用梯度下降的优化方法
all_theta[:,i] = result.reshape(1,-1) # 放入all_theta中
all_theta = np.transpose(all_theta)
return all_theta
```
4、预测
-
之前说过,预测的结果是一个
概率值
,利用学习出来的
theta代入预测的 S 型函数 中,每行的最大值就是是某个数字的最大概率,所在的 列号 就是预测的数字的真实值,因为在分类时,所有为0的将y映射在第一列,为 1 的映射在第二列,依次类推 - 实现代码:
```
预测
def predict_oneVsAll(all_theta,X): m = X.shape[0] num_labels = all_theta.shape[0] p = np.zeros((m,1)) X = np.hstack((np.ones((m,1)),X)) #在X最前面加一列1
h = sigmoid(np.dot(X,np.transpose(all_theta))) #预测
'''
返回h中每一行最大值所在的列号
- np.max(h, axis=1)返回h中每一行的最大值(是某个数字的最大概率)
- 最后where找到的最大概率所在的列号(列号即是对应的数字)
'''
p = np.array(np.where(h[0,:] == np.max(h, axis=1)[0]))
for i in np.arange(1, m):
t = np.array(np.where(h[i,:] == np.max(h, axis=1)[i]))
p = np.vstack((p,t))
return p
```
5、运行结果
-
10 次分类,在训练集上的准确度:

6、 使用 scikit-learn 库中的逻辑回归模型实现
- 1、导入包
from scipy import io as spio
import numpy as np
from sklearn import svm
from sklearn.linear_model import LogisticRegression
- 2、加载数据
data = loadmat_data("data_digits.mat")
X = data['X'] # 获取X数据,每一行对应一个数字20x20px
y = data['y'] # 这里读取mat文件y的shape=(5000, 1)
y = np.ravel(y) # 调用sklearn需要转化成一维的(5000,)
- 3、拟合模型
model = LogisticRegression()
model.fit(X, y) # 拟合
- 4、预测
``` predict = model.predict(X) #预测
print u"预测准确度为:%f%%"%np.mean(np.float64(predict == y)*100)
```
-
5、输出结果(在训练集上的准确度)

三、BP 神经网络
1、神经网络 model
- 先介绍个三层的神经网络,如下图所示
-
输入层(input layer)有三个 units(
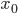 为补上的 bias,通常设为
为补上的 bias,通常设为
1) -
 表示第
表示第
j层的第i个激励,也称为为单元 unit -
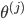 为第
为第
j层到第j+1层映射的权重矩阵,就是每条边的权重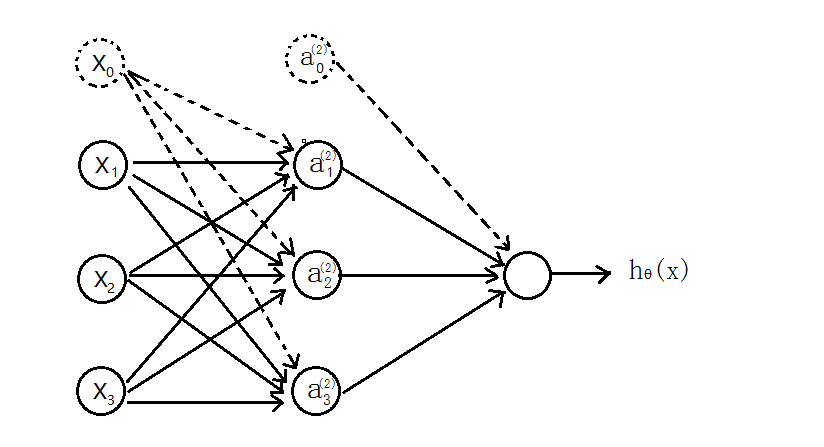
- 所以可以得到:
-
隐含层:
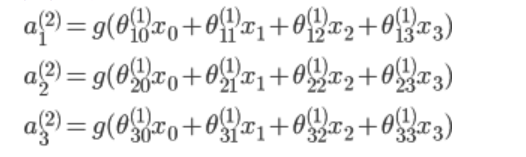
-
输出层
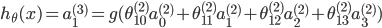 其中,
S 型函数
其中,
S 型函数
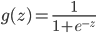 ,也成为
激励函数
,也成为
激励函数
-
可以看出
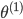 为 3x4 的矩阵,
为 3x4 的矩阵,
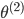 为 1x4 的矩阵
为 1x4 的矩阵
-
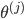 ==》
==》
j+1的单元数 x(j层的单元数 +1)
2、代价函数
-
假设最后输出的
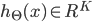 ,即代表输出层有 K 个单元
,即代表输出层有 K 个单元
-
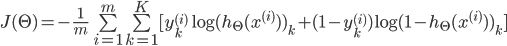 其中,
其中,
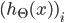 代表第
代表第
i个单元输出 -
与逻辑回归的代价函数
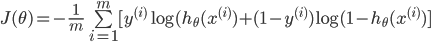 差不多,就是累加上每个输出(共有 K 个输出)
差不多,就是累加上每个输出(共有 K 个输出)
3、正则化
-
L--> 所有层的个数 -
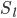 --> 第
--> 第
l层 unit 的个数 -
正则化后的
代价函数
为
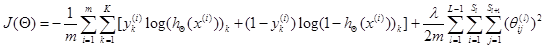
-
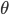 共有
共有
L-1层, - 然后是累加对应每一层的 theta 矩阵,注意不包含加上偏置项对应的 theta(0)
- 正则化后的代价函数实现代码:
```
代价函数
def nnCostFunction(nn_params,input_layer_size,hidden_layer_size,num_labels,X,y,Lambda): length = nn_params.shape[0] # theta的中长度 # 还原theta1和theta2 Theta1 = nn_params[0:hidden_layer_size (input_layer_size+1)].reshape(hidden_layer_size,input_layer_size+1) Theta2 = nn_params[hidden_layer_size (input_layer_size+1):length].reshape(num_labels,hidden_layer_size+1)
# np.savetxt("Theta1.csv",Theta1,delimiter=',')
m = X.shape[0]
class_y = np.zeros((m,num_labels)) # 数据的y对应0-9,需要映射为0/1的关系
# 映射y
for i in range(num_labels):
class_y[:,i] = np.int32(y==i).reshape(1,-1) # 注意reshape(1,-1)才可以赋值
'''去掉theta1和theta2的第一列,因为正则化时从1开始'''
Theta1_colCount = Theta1.shape[1]
Theta1_x = Theta1[:,1:Theta1_colCount]
Theta2_colCount = Theta2.shape[1]
Theta2_x = Theta2[:,1:Theta2_colCount]
# 正则化向theta^2
term = np.dot(np.transpose(np.vstack((Theta1_x.reshape(-1,1),Theta2_x.reshape(-1,1)))),np.vstack((Theta1_x.reshape(-1,1),Theta2_x.reshape(-1,1))))
'''正向传播,每次需要补上一列1的偏置bias'''
a1 = np.hstack((np.ones((m,1)),X))
z2 = np.dot(a1,np.transpose(Theta1))
a2 = sigmoid(z2)
a2 = np.hstack((np.ones((m,1)),a2))
z3 = np.dot(a2,np.transpose(Theta2))
h = sigmoid(z3)
'''代价'''
J = -(np.dot(np.transpose(class_y.reshape(-1,1)),np.log(h.reshape(-1,1)))+np.dot(np.transpose(1-class_y.reshape(-1,1)),np.log(1-h.reshape(-1,1)))-Lambda*term/2)/m
return np.ravel(J)
```
4、反向传播 BP
-
上面正向传播可以计算得到
J(θ),使用梯度下降法还需要求它的梯度 - BP 反向传播的目的就是求代价函数的梯度
-
假设 4 层的神经网络,
 记为-->
记为-->
l层第j个单元的误差 -

-
没有
 ,因为对于输入没有误差
,因为对于输入没有误差
-

- 反向传播计算梯度的过程为:
-

-

-
最后
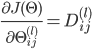 ,即得到代价函数的梯度
,即得到代价函数的梯度
- 实现代码:
```
梯度
def nnGradient(nn_params,input_layer_size,hidden_layer_size,num_labels,X,y,Lambda):
length = nn_params.shape[0]
Theta1 = nn_params[0:hidden_layer_size
(input_layer_size+1)].reshape(hidden_layer_size,input_layer_size+1).copy() # 这里使用copy函数,否则下面修改Theta的值,nn_params也会一起修改
Theta2 = nn_params[hidden_layer_size
(input_layer_size+1):length].reshape(num_labels,hidden_layer_size+1).copy()
m = X.shape[0]
class_y = np.zeros((m,num_labels)) # 数据的y对应0-9,需要映射为0/1的关系
# 映射y
for i in range(num_labels):
class_y[:,i] = np.int32(y==i).reshape(1,-1) # 注意reshape(1,-1)才可以赋值
'''去掉theta1和theta2的第一列,因为正则化时从1开始'''
Theta1_colCount = Theta1.shape[1]
Theta1_x = Theta1[:,1:Theta1_colCount]
Theta2_colCount = Theta2.shape[1]
Theta2_x = Theta2[:,1:Theta2_colCount]
Theta1_grad = np.zeros((Theta1.shape)) #第一层到第二层的权重
Theta2_grad = np.zeros((Theta2.shape)) #第二层到第三层的权重
'''正向传播,每次需要补上一列1的偏置bias'''
a1 = np.hstack((np.ones((m,1)),X))
z2 = np.dot(a1,np.transpose(Theta1))
a2 = sigmoid(z2)
a2 = np.hstack((np.ones((m,1)),a2))
z3 = np.dot(a2,np.transpose(Theta2))
h = sigmoid(z3)
'''反向传播,delta为误差,'''
delta3 = np.zeros((m,num_labels))
delta2 = np.zeros((m,hidden_layer_size))
for i in range(m):
#delta3[i,:] = (h[i,:]-class_y[i,:])*sigmoidGradient(z3[i,:]) # 均方误差的误差率
delta3[i,:] = h[i,:]-class_y[i,:] # 交叉熵误差率
Theta2_grad = Theta2_grad+np.dot(np.transpose(delta3[i,:].reshape(1,-1)),a2[i,:].reshape(1,-1))
delta2[i,:] = np.dot(delta3[i,:].reshape(1,-1),Theta2_x)*sigmoidGradient(z2[i,:])
Theta1_grad = Theta1_grad+np.dot(np.transpose(delta2[i,:].reshape(1,-1)),a1[i,:].reshape(1,-1))
Theta1[:,0] = 0
Theta2[:,0] = 0
'''梯度'''
grad = (np.vstack((Theta1_grad.reshape(-1,1),Theta2_grad.reshape(-1,1)))+Lambda*np.vstack((Theta1.reshape(-1,1),Theta2.reshape(-1,1))))/m
return np.ravel(grad)
```
5、BP 可以求梯度的原因
-
实际是利用了
链式求导法则 - 因为下一层的单元利用上一层的单元作为输入进行计算
-
大体的推导过程如下,最终我们是想预测函数与已知的
y非常接近,求均方差的梯度沿着此梯度方向可使代价函数最小化。可对照上面求梯度的过程。
-
求误差更详细的推导过程:
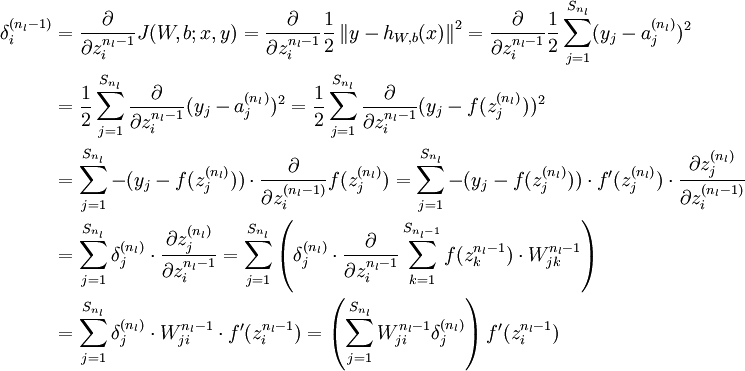
6、梯度检查
-
检查利用
BP求的梯度是否正确 -
利用导数的定义验证:
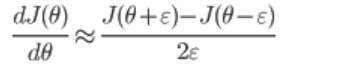
- 求出来的数值梯度应该与 BP 求出的梯度非常接近
- 验证 BP 正确后就不需要再执行验证梯度的算法了
- 实现代码:
```
检验梯度是否计算正确
检验梯度是否计算正确
def checkGradient(Lambda = 0): '''构造一个小型的神经网络验证,因为数值法计算梯度很浪费时间,而且验证正确后之后就不再需要验证了''' input_layer_size = 3 hidden_layer_size = 5 num_labels = 3 m = 5 initial_Theta1 = debugInitializeWeights(input_layer_size,hidden_layer_size); initial_Theta2 = debugInitializeWeights(hidden_layer_size,num_labels) X = debugInitializeWeights(input_layer_size-1,m) y = 1+np.transpose(np.mod(np.arange(1,m+1), num_labels))# 初始化y
y = y.reshape(-1,1)
nn_params = np.vstack((initial_Theta1.reshape(-1,1),initial_Theta2.reshape(-1,1))) #展开theta
'''BP求出梯度'''
grad = nnGradient(nn_params, input_layer_size, hidden_layer_size,
num_labels, X, y, Lambda)
'''使用数值法计算梯度'''
num_grad = np.zeros((nn_params.shape[0]))
step = np.zeros((nn_params.shape[0]))
e = 1e-4
for i in range(nn_params.shape[0]):
step[i] = e
loss1 = nnCostFunction(nn_params-step.reshape(-1,1), input_layer_size, hidden_layer_size,
num_labels, X, y,
Lambda)
loss2 = nnCostFunction(nn_params+step.reshape(-1,1), input_layer_size, hidden_layer_size,
num_labels, X, y,
Lambda)
num_grad[i] = (loss2-loss1)/(2*e)
step[i]=0
# 显示两列比较
res = np.hstack((num_grad.reshape(-1,1),grad.reshape(-1,1)))
print res
```
7、权重的随机初始化
-
神经网络不能像逻辑回归那样初始化
theta为0,因为若是每条边的权重都为 0,每个神经元都是相同的输出,在反向传播中也会得到同样的梯度,最终只会预测一种结果。 - 所以应该初始化为接近 0 的数
- 实现代码
```
随机初始化权重theta
def randInitializeWeights(L_in,L_out): W = np.zeros((L_out,1+L_in)) # 对应theta的权重 epsilon_init = (6.0/(L_out+L_in)) 0.5 W = np.random.rand(L_out,1+L_in) 2 epsilon_init-epsilon_init # np.random.rand(L_out,1+L_in)产生L_out*(1+L_in)大小的随机矩阵 return W ```
8、预测
- 正向传播预测结果
- 实现代码
```
预测
def predict(Theta1,Theta2,X): m = X.shape[0] num_labels = Theta2.shape[0] #p = np.zeros((m,1)) '''正向传播,预测结果''' X = np.hstack((np.ones((m,1)),X)) h1 = sigmoid(np.dot(X,np.transpose(Theta1))) h1 = np.hstack((np.ones((m,1)),h1)) h2 = sigmoid(np.dot(h1,np.transpose(Theta2)))
'''
返回h中每一行最大值所在的列号
- np.max(h, axis=1)返回h中每一行的最大值(是某个数字的最大概率)
- 最后where找到的最大概率所在的列号(列号即是对应的数字)
'''
#np.savetxt("h2.csv",h2,delimiter=',')
p = np.array(np.where(h2[0,:] == np.max(h2, axis=1)[0]))
for i in np.arange(1, m):
t = np.array(np.where(h2[i,:] == np.max(h2, axis=1)[i]))
p = np.vstack((p,t))
return p
```
9、输出结果
-
梯度检查:
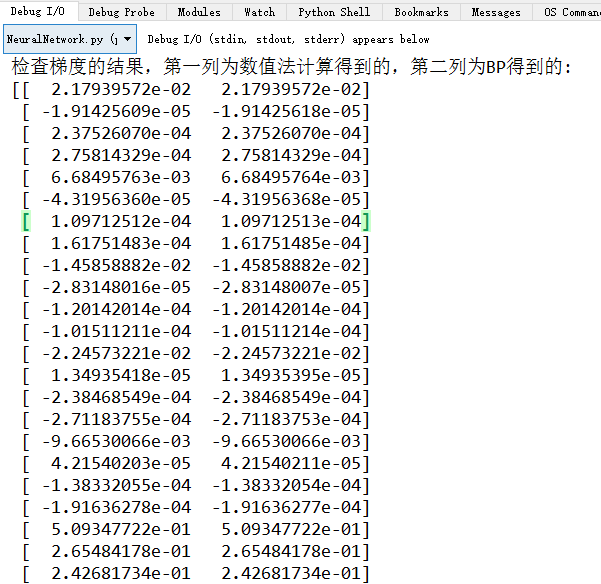
-
随机显示 100 个手写数字

-
显示 theta1 权重
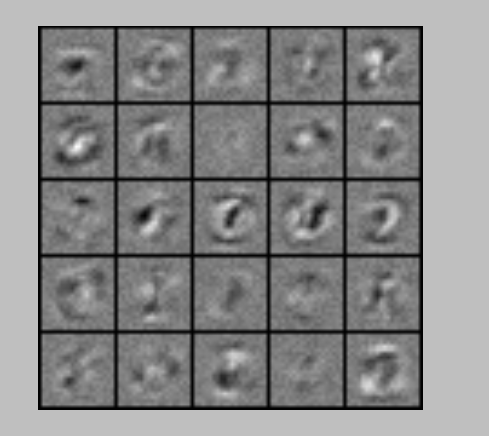
-
训练集预测准确度

-
归一化后训练集预测准确度

四、SVM 支持向量机
1、代价函数
-
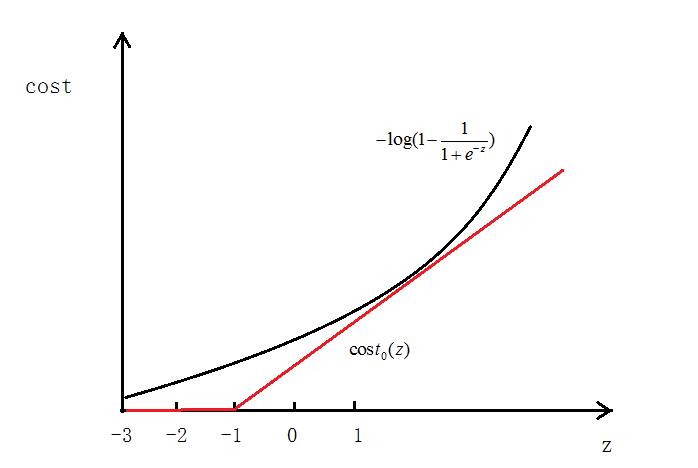
在逻辑回归中,我们的代价为:

-
如图所示,如果
y=1,cost代价函数如图所示

-
当
y=0时同样,用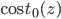 代替
代替
-
最终得到的代价函数为:
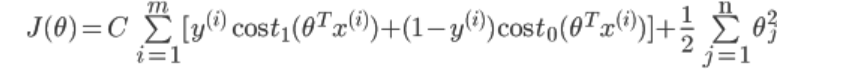 最后我们想要
最后我们想要
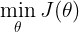
-
之前我们逻辑回归中的代价函数为:
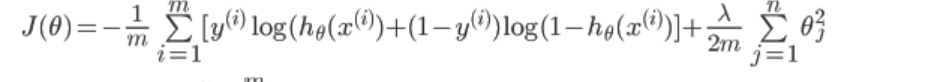 可以认为这里的
可以认为这里的
 ,只是表达形式问题,这里
,只是表达形式问题,这里
C的值越大,SVM 的决策边界的margin也越大,下面会说明
2、Large Margin
-
如下图所示,SVM 分类会使用最大的
margin将其分开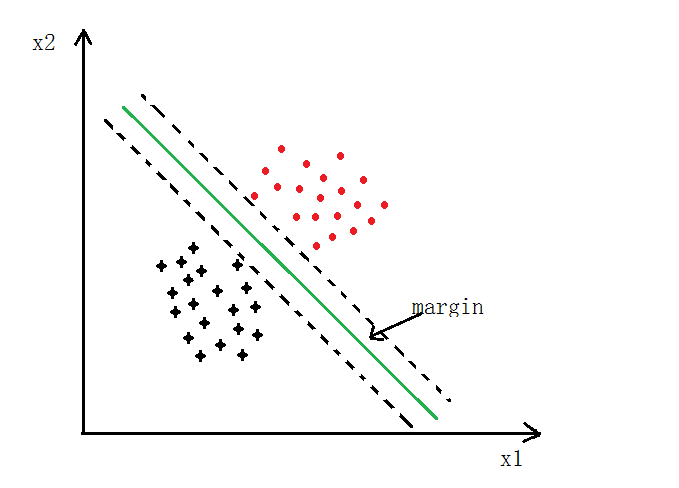
- 先说一下向量内积
-

-

-
向量V在向量u上的投影的长度记为p,则:向量内积:
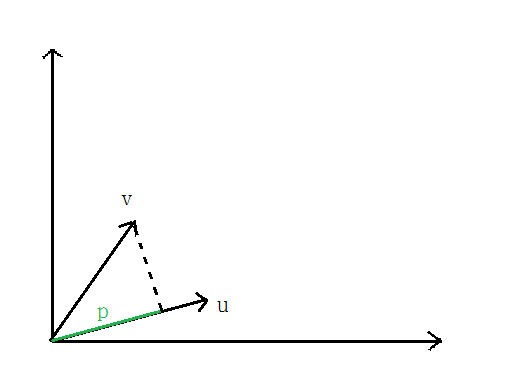 根据向量夹角公式推导一下即可,
根据向量夹角公式推导一下即可,
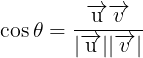
-
前面说过,当
C越大时,margin也就越大,我们的目的是最小化代价函数J(θ),当margin最大时,C的乘积项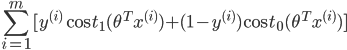 要很小,所以近似为:
要很小,所以近似为:
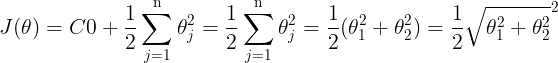 ,
我们最后的目的就是求使代价最小的
,
我们最后的目的就是求使代价最小的
θ -
由
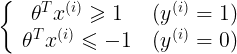 可以得到:
可以得到:
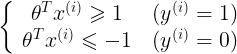 ,
,
p即为x在θ上的投影 -
如下图所示,假设决策边界如图,找其中的一个点,到
θ上的投影为p,则 或者
或者
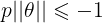 ,若是
,若是
p很小,则需要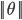 很大,最后求的是
很大,最后求的是
large margin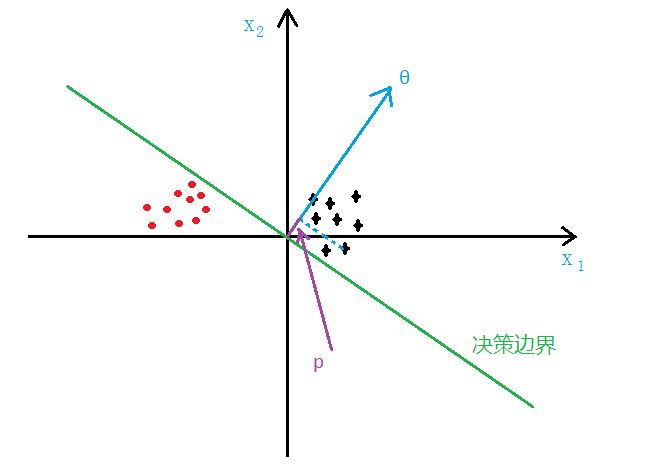
3、SVM Kernel(核函数)

-
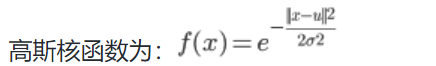
- 假设如图几个点,
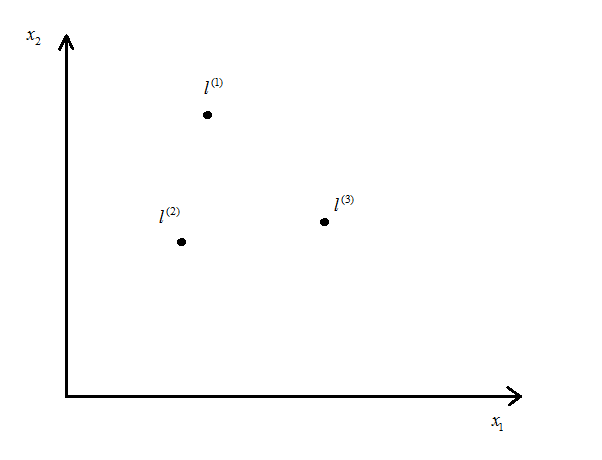
令
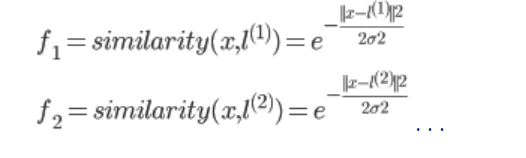
-
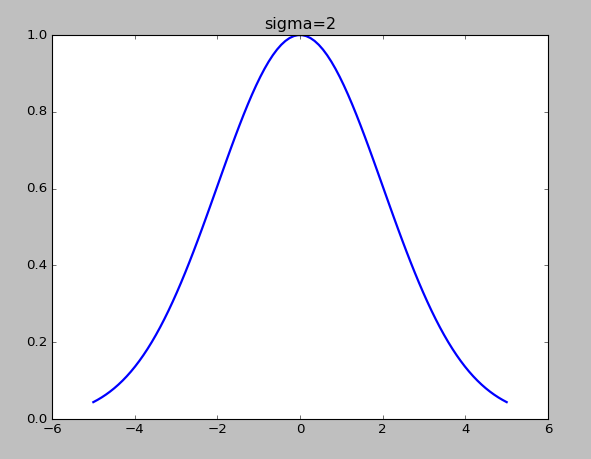
高斯核函数的
σ越小,f下降的越快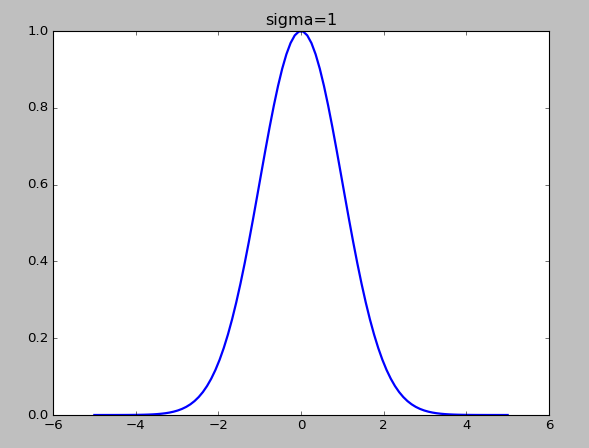
-
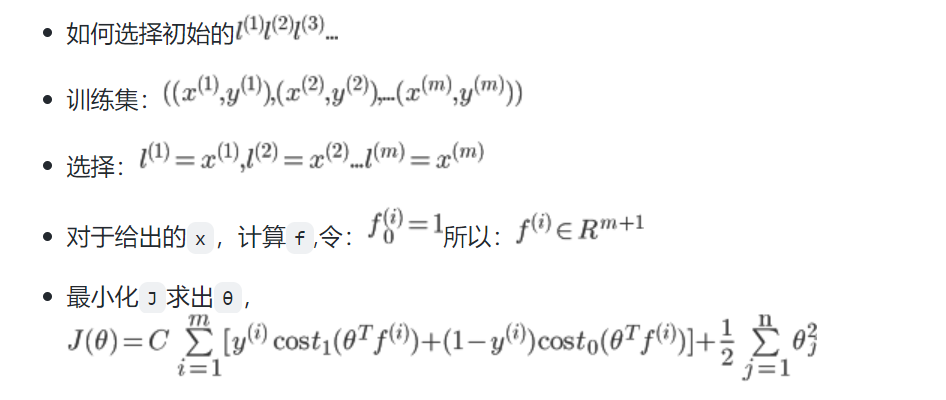
-
最小化
J求出θ,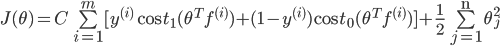
-
如果
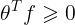 ,==》预测
,==》预测
y=1
4、使用
scikit-learn
中的
SVM
模型代码
- 全部代码
-
线性可分的,指定核函数为
linear:
``` '''data1——线性分类''' data1 = spio.loadmat('data1.mat') X = data1['X'] y = data1['y'] y = np.ravel(y) plot_data(X,y)
model = svm.SVC(C=1.0,kernel='linear').fit(X,y) # 指定核函数为线性核函数
```
-
非线性可分的,默认核函数为
rbf
``` '''data2——非线性分类''' data2 = spio.loadmat('data2.mat') X = data2['X'] y = data2['y'] y = np.ravel(y) plt = plot_data(X,y) plt.show()
model = svm.SVC(gamma=100).fit(X,y) # gamma为核函数的系数,值越大拟合的越好
```
5、运行结果
-
线性可分的决策边界:
-
线性不可分的决策边界:

五、K-Means 聚类算法
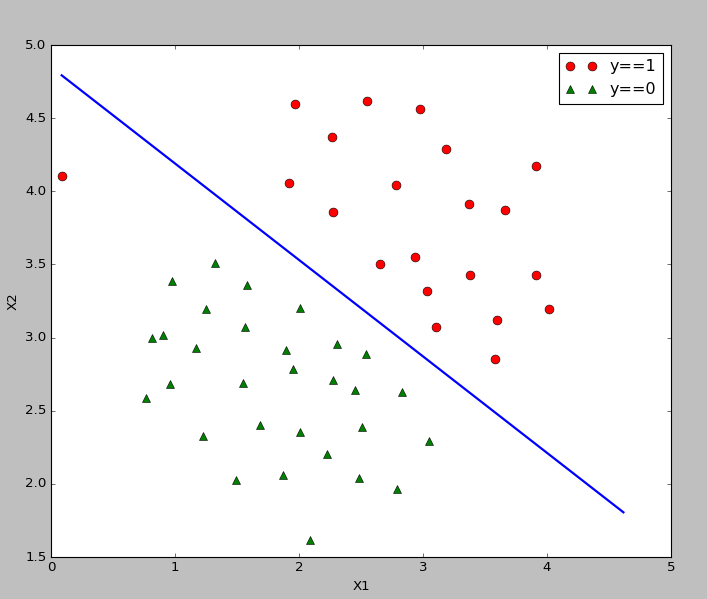
1、聚类过程
- 聚类属于无监督学习,不知道 y 的标记分为 K 类
- K-Means 算法分为两个步骤
-
第一步:簇分配,随机选
K个点作为中心,计算到这K个点的距离,分为K个簇 - 第二步:移动聚类中心:重新计算每个 簇 的中心,移动中心,重复以上步骤。
- 如下图所示:
- 随机分配的聚类中心
 - 重新计算聚类中心,移动一次
- 重新计算聚类中心,移动一次
 - 最后
- 最后
10
步之后的聚类中心
 - 计算每条数据到哪个中心最近实现代码:
- 计算每条数据到哪个中心最近实现代码:
```
找到每条数据距离哪个类中心最近
def findClosestCentroids(X,initial_centroids): m = X.shape[0] # 数据条数 K = initial_centroids.shape[0] # 类的总数 dis = np.zeros((m,K)) # 存储计算每个点分别到K个类的距离 idx = np.zeros((m,1)) # 要返回的每条数据属于哪个类
'''计算每个点到每个类中心的距离'''
for i in range(m):
for j in range(K):
dis[i,j] = np.dot((X[i,:]-initial_centroids[j,:]).reshape(1,-1),(X[i,:]-initial_centroids[j,:]).reshape(-1,1))
'''返回dis每一行的最小值对应的列号,即为对应的类别
- np.min(dis, axis=1)返回每一行的最小值
- np.where(dis == np.min(dis, axis=1).reshape(-1,1)) 返回对应最小值的坐标
- 注意:可能最小值对应的坐标有多个,where都会找出来,所以返回时返回前m个需要的即可(因为对于多个最小值,属于哪个类别都可以)
'''
dummy,idx = np.where(dis == np.min(dis, axis=1).reshape(-1,1))
return idx[0:dis.shape[0]] # 注意截取一下
```
- 计算类中心实现代码:
```
计算类中心
def computerCentroids(X,idx,K): n = X.shape[1] centroids = np.zeros((K,n)) for i in range(K): centroids[i,:] = np.mean(X[np.ravel(idx==i),:], axis=0).reshape(1,-1) # 索引要是一维的,axis=0为每一列,idx==i一次找出属于哪一类的,然后计算均值 return centroids ```
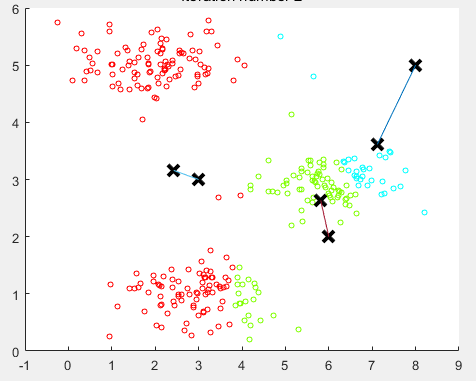
2、目标函数
- 也叫做 失真代价函数
-
-
最后我们想得到:
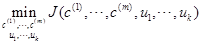
-
其中
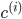 表示第
表示第
i条数据距离哪个类中心最近, -
其中
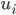 即为聚类的中心
即为聚类的中心
3、聚类中心的选择
- 随机初始化,从给定的数据中随机抽取 K 个作为聚类中心
- 随机一次的结果可能不好,可以随机多次,最后取使代价函数最小的作为中心
- 实现代码:(这里随机一次)
```
初始化类中心--随机取K个点作为聚类中心
def kMeansInitCentroids(X,K):
m = X.shape[0]
m_arr = np.arange(0,m) # 生成0-m-1
centroids = np.zeros((K,X.shape[1]))
np.random.shuffle(m_arr) # 打乱m_arr顺序
rand_indices = m_arr[:K] # 取前K个
centroids = X[rand_indices,:]
return centroids
```
4、聚类个数 K 的选择
- 聚类是不知道 y 的 label 的,所以不知道真正的聚类个数
- 肘部法则(Elbow method)
-
作代价函数
J和K的图,若是出现一个拐点,如下图所示,K就取拐点处的值,下图此时K=3
- 若是很平滑就不明确,人为选择。
- 第二种就是人为观察选择
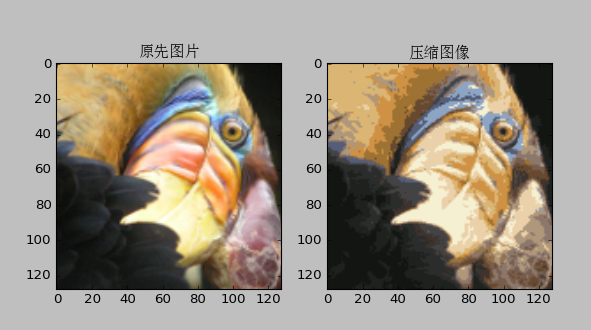
5、应用——图片压缩
- 将图片的像素分为若干类,然后用这个类代替原来的像素值
- 执行聚类的算法代码:
```
聚类算法
def runKMeans(X,initial_centroids,max_iters,plot_process): m,n = X.shape # 数据条数和维度 K = initial_centroids.shape[0] # 类数 centroids = initial_centroids # 记录当前类中心 previous_centroids = centroids # 记录上一次类中心 idx = np.zeros((m,1)) # 每条数据属于哪个类
for i in range(max_iters): # 迭代次数
print u'迭代计算次数:%d'%(i+1)
idx = findClosestCentroids(X, centroids)
if plot_process: # 如果绘制图像
plt = plotProcessKMeans(X,centroids,previous_centroids) # 画聚类中心的移动过程
previous_centroids = centroids # 重置
centroids = computerCentroids(X, idx, K) # 重新计算类中心
if plot_process: # 显示最终的绘制结果
plt.show()
return centroids,idx # 返回聚类中心和数据属于哪个类
```
6、 使用 scikit-learn 库中的线性模型实现聚类
- 导入包
from sklearn.cluster import KMeans
- 使用模型拟合数据
model = KMeans(n_clusters=3).fit(X) # n_clusters指定3类,拟合数据
- 聚类中心
centroids = model.cluster_centers_ # 聚类中心
7、运行结果
-
二维数据类中心的移动

-
图片压缩
六、PCA 主成分分析(降维)
1、用处
- 数据压缩(Data Compression),使程序运行更快
-
可视化数据,例如
3D-->2D等 - ......
2、2D-->1D,nD-->kD
-
如下图所示,所有数据点可以投影到一条直线,是
投影距离的平方和
(投影误差)最小
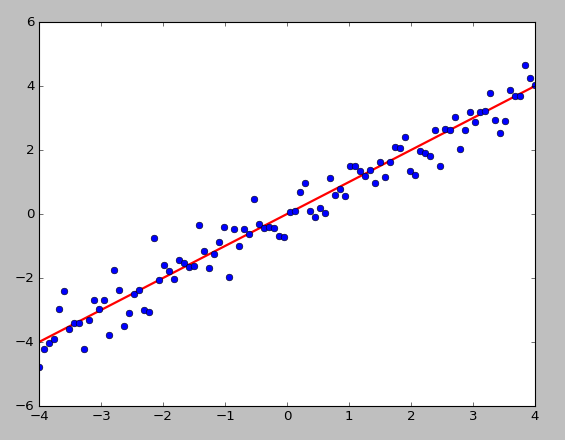
-
注意数据需要
归一化处理 -
思路是找
1个向量u,所有数据投影到上面使投影距离最小 -
那么
nD-->kD就是找k个向量,所有数据投影到上面使投影误差最小 - eg:3D-->2D,2 个向量就代表一个平面了,所有点投影到这个平面的投影误差最小即可
3、主成分分析 PCA 与线性回归的区别
-
线性回归是找
x与y的关系,然后用于预测y -
PCA是找一个投影面,最小化 data 到这个投影面的投影误差
4、PCA 降维过程
- 数据预处理(均值归一化)
- 就是减去对应 feature 的均值,然后除以对应特征的标准差(也可以是最大值-最小值)
- 实现代码:
``` # 归一化数据 def featureNormalize(X): '''(每一个数据-当前列的均值)/当前列的标准差''' n = X.shape[1] mu = np.zeros((1,n)); sigma = np.zeros((1,n))
mu = np.mean(X,axis=0)
sigma = np.std(X,axis=0)
for i in range(n):
X[:,i] = (X[:,i]-mu[i])/sigma[i]
return X,mu,sigma
```
-
注意这里的
Σ和求和符号不同 -
协方差矩阵
对称正定(不理解正定的看看线代) -
大小为
nxn,n为feature的维度 - 实现代码:
Sigma = np.dot(np.transpose(X_norm),X_norm)/m # 求Sigma
-
计算
Σ的特征值和特征向量 -
可以是用
svd奇异值分解函数:U,S,V = svd(Σ) -
返回的是与
Σ同样大小的对角阵S(由Σ的特征值组成)[ 注意 :matlab中函数返回的是对角阵,在python中返回的是一个向量,节省空间] - 还有两个 酉矩阵 U 和 V
-
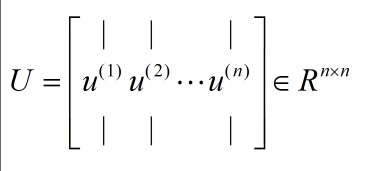
-
注意
:
svd函数求出的S是按特征值降序排列的,若不是使用svd,需要按 特征值 大小重新排列U - 降维
-
选取
U中的前K列(假设要降为K维) -
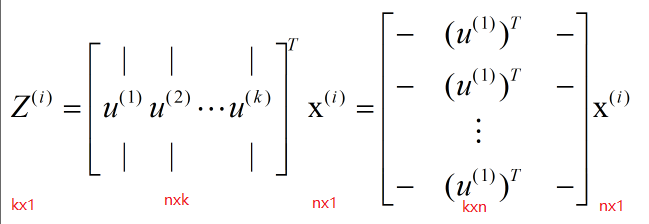
-
Z就是对应降维之后的数据 - 实现代码:
``` # 映射数据 def projectData(X_norm,U,K): Z = np.zeros((X_norm.shape[0],K))
U_reduce = U[:,0:K] # 取前K个
Z = np.dot(X_norm,U_reduce)
return Z
```
- 过程总结:
-
Sigma = X'*X/m -
U,S,V = svd(Sigma) -
Ureduce = U[:,0:k] -
Z = Ureduce'*x
5、数据恢复
- 实现代码:
# 恢复数据
def recoverData(Z,U,K):
X_rec = np.zeros((Z.shape[0],U.shape[0]))
U_recude = U[:,0:K]
X_rec = np.dot(Z,np.transpose(U_recude)) # 还原数据(近似)
return X_rec
6、主成分个数的选择(即要降的维度)
- 如何选择
-
误差率一般取
1%,5%,10%等 - 如何实现
- 若是一个个试的话代价太大
-
可以一点点增加
K尝试。
7、使用建议
-
不要使用 PCA 去解决过拟合问题
Overfitting,还是使用正则化的方法(如果保留了很高的差异性还是可以的) - 只有在原数据上有好的结果,但是运行很慢,才考虑使用 PCA
8、运行结果
- 2 维数据降为 1 维
-
要投影的方向

-
2D 降为 1D 及对应关系
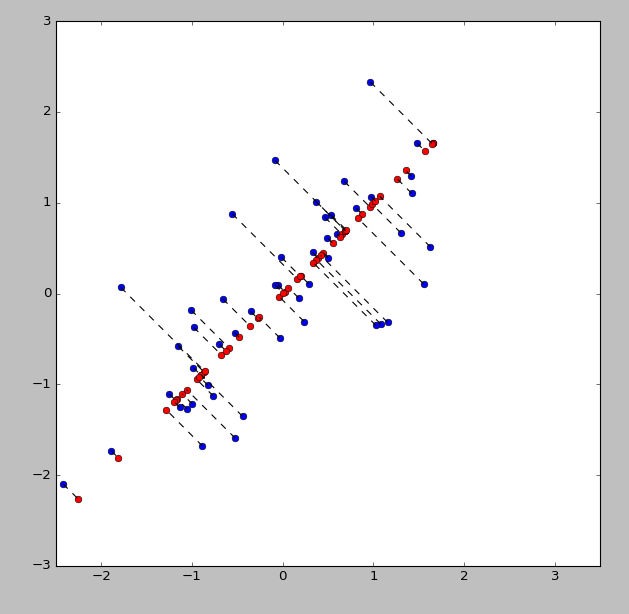
- 人脸数据降维
-
原始数据

-
可视化部分
U矩阵信息
 - 恢复数据
- 恢复数据

9、 使用 scikit-learn 库中的 PCA 实现降维
- 导入需要的包:
```
- - coding: utf-8 - -
Author:bob
Date:2016.12.22
import numpy as np from matplotlib import pyplot as plt from scipy import io as spio from sklearn.decomposition import pca from sklearn.preprocessing import StandardScaler ```
- 归一化数据
'''归一化数据并作图'''
scaler = StandardScaler()
scaler.fit(X)
x_train = scaler.transform(X)
- 使用 PCA 模型拟合数据,并降维
-
n_components对应要将的维度
'''拟合数据'''
K=1 # 要降的维度
model = pca.PCA(n_components=K).fit(x_train) # 拟合数据,n_components定义要降的维度
Z = model.transform(x_train) # transform就会执行降维操作
- 数据恢复
-
model.components_会得到降维使用的U矩阵
'''数据恢复并作图'''
Ureduce = model.components_ # 得到降维用的Ureduce
x_rec = np.dot(Z,Ureduce) # 数据恢复
七、异常检测 Anomaly Detection
1、高斯分布(正态分布)
Gaussian distribution
-
其中,
u为数据的 均值 ,σ为数据的 标准差 -
σ越 小 ,对应的图像越 尖
2、异常检测算法
- 例子
-
计算
p(x),若是P(x)<ε则认为异常,其中ε为我们要求的概率的临界值threshold -
这里只是
单元高斯分布
,假设了
feature之间是独立的,下面会讲到 多元高斯分布 ,会自动捕捉到feature之间的关系 - 参数估计 实现代码
```
参数估计函数(就是求均值和方差)
def estimateGaussian(X): m,n = X.shape mu = np.zeros((n,1)) sigma2 = np.zeros((n,1))
mu = np.mean(X, axis=0) # axis=0表示列,每列的均值
sigma2 = np.var(X,axis=0) # 求每列的方差
return mu,sigma2
```
3、评价
p(x)
的好坏,以及
ε
的选取
- 对 偏斜数据 的错误度量
-
因为数据可能是非常
偏斜
的(就是
y=1的个数非常少,(y=1表示异常)),所以可以使用Precision/Recall,计算F1Score(在 CV 交叉验证集 上) -
例如:预测癌症,假设模型可以得到
99%能够预测正确,1%的错误率,但是实际癌症的概率很小,只有0.5%,那么我们始终预测没有癌症 y=0 反而可以得到更小的错误率。使用error rate来评估就不科学了。 -
如下图记录:
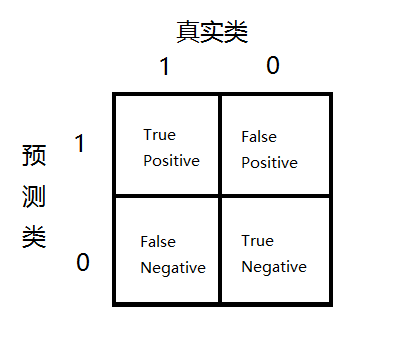
- 还是以癌症预测为例,假设预测都是 no-cancer,TN=199,FN=1,TP=0,FP=0,所以:Precision=0/0,Recall=0/1=0,尽管 accuracy=199/200=99.5%,但是不可信。
-
ε的选取 -
尝试多个
ε值,使F1Score的值高 - 实现代码
```
选择最优的epsilon,即:使F1Score最大
def selectThreshold(yval,pval):
'''初始化所需变量'''
bestEpsilon = 0.
bestF1 = 0.
F1 = 0.
step = (np.max(pval)-np.min(pval))/1000
'''计算'''
for epsilon in np.arange(np.min(pval),np.max(pval),step):
cvPrecision = pval
4、选择使用什么样的 feature(单元高斯分布)
-
如果一些数据不是满足高斯分布的,可以变化一下数据,例如
log(x+C),x^(1/2)等 -
如果
p(x)的值无论异常与否都很大,可以尝试组合多个feature,(因为 feature 之间可能是有关系的)
5、多元高斯分布
- 单元高斯分布存在的问题
-
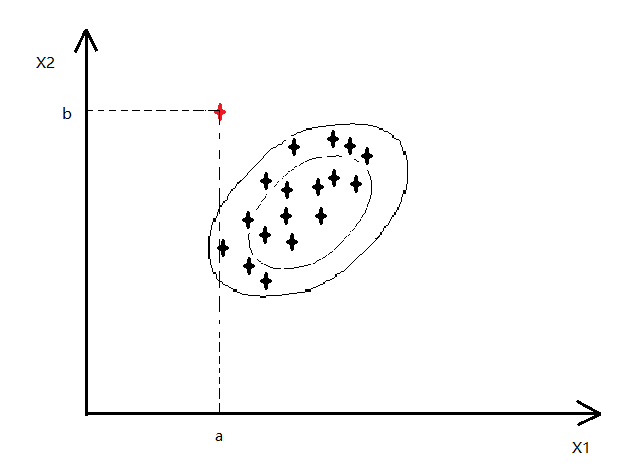
如下图,红色的点为异常点,其他的都是正常点(比如 CPU 和 memory 的变化)
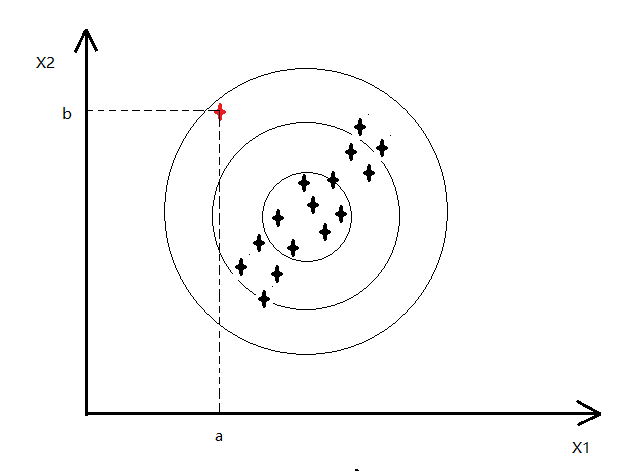
-
x1 对应的高斯分布如下:
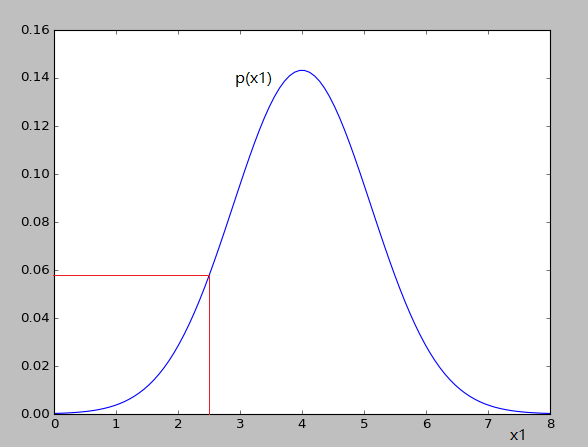
-
x2 对应的高斯分布如下:
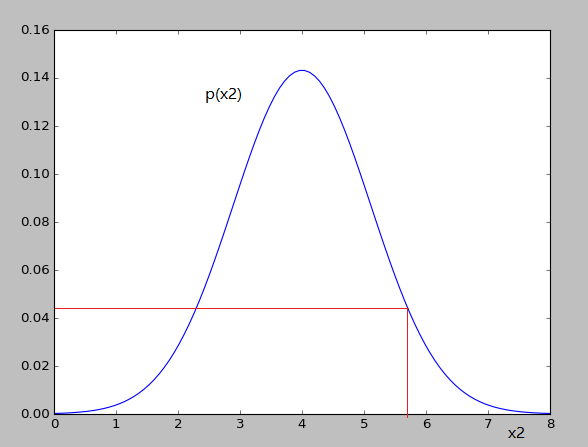
- 可以看出对应的 p(x1)和 p(x2)的值变化并不大,就不会认为异常
- 因为我们认为 feature 之间是相互独立的,所以如上图是以 正圆 的方式扩展
-
例如:
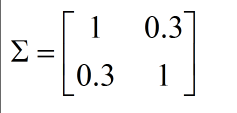
表示 x1,x2
正相关
,即 x1 越大,x2 也就越大,如下图,也就可以将红色的异常点检查出了
 若:
若:
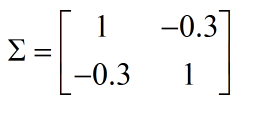 表示 x1,x2
负相关
- 实现代码:
表示 x1,x2
负相关
- 实现代码:
```
多元高斯分布函数
def multivariateGaussian(X,mu,Sigma2):
k = len(mu)
if (Sigma2.shape[0]>1):
Sigma2 = np.diag(Sigma2)
'''多元高斯分布函数'''
X = X-mu
argu = (2
np.pi)
(-k/2)
np.linalg.det(Sigma2)
(-0.5)
p = argu
np.exp(-0.5
np.sum(np.dot(X,np.linalg.inv(Sigma2))*X,axis=1)) # axis表示每行
return p
```
6、单元和多元高斯分布特点
- 单元高斯分布
-
人为可以捕捉到
feature之间的关系时可以使用 - 计算量小
- 多元高斯分布
- 自动捕捉到相关的 feature
-
m>n或Σ可逆时可以使用。(若不可逆,可能有冗余的 x,因为线性相关,不可逆,或者就是 m<n)
7、程序运行结果
-
显示数据
-
等高线
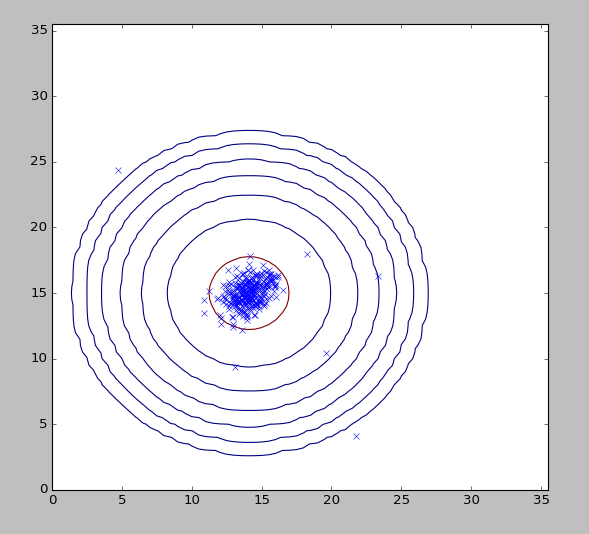
-
异常点标注

参考文献
- 视频处理平台的设计与实现(北京交通大学·时月月)
- 推荐系统协同过滤算法的改进(云南大学·石婷)
- 中学python课程知识图谱构建及应用研究(华中师范大学·黄健)
- 基于深度学习知识追踪模型的在线教育数据挖掘研究(哈尔滨工业大学·徐盛原)
- 基于Wide&Deep的在线学习资源推荐算法研究(西南大学·刘捷)
- 基于数据挖掘的电视节目个性化推荐研究及实现(曲阜师范大学·徐晟杰)
- 数据预测的图形化编程及应用(青海师范大学·林连海)
- 基于Wide&Deep的在线学习资源推荐算法研究(西南大学·刘捷)
- 基于Lucene的商品垂直搜索引擎研究与实现(东华大学·潘磊宁)
- 基于商品名称的电商平台商品自动分类的研究与实现(西南交通大学·黄超)
- 机器学习应用开发平台的设计与实现(西安电子科技大学·邢璐)
- 基于自然语言的移动机器人任务理解研究与实现(南京理工大学·柴亚登)
- 基于数据挖掘的电视节目个性化推荐研究及实现(曲阜师范大学·徐晟杰)
- 基于AI的去中心化在线学习系统的研究(江苏科技大学·王启亮)
- 中学python课程知识图谱构建及应用研究(华中师范大学·黄健)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:代码驿站 ,原文地址:https://m.bishedaima.com/yuanma/35797.html