广度优先遍历搜索(BFS)
1 算法介绍
广度优先搜索算法(英语:Breadth-First-Search,缩写为 BFS),是一种图形搜索算法。简单的说,BFS 是从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。BFS 是一种盲目搜索法,目的是系统地展开并检查图中的所有节点,以找寻结果。
BFS 会先访问根节点的所有邻居节点,然后再依次访问邻居节点的邻居节点,直到所有节点都访问完毕。在具体的实现中,使用 open 和 closed 两个表,open 是一个队列,每次对 open 进行一次出队操作(并放入 closed 中),并将其邻居节点进行入队操作。直到队列为空时即完成了所有节点的遍历。closed 表在遍历树时其实没有用,因为子节点只能从父节点到达。但在进行图的遍历时,一个节点可能会由多个节点到达,所以此时为了防止重复遍历应该每次都检查下一个节点是否已经在 closed 中了。
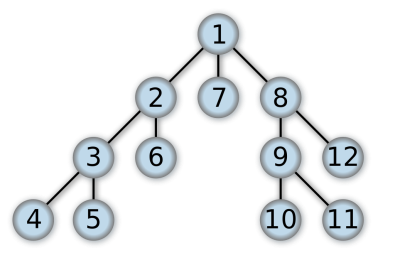
依然使用上面的这个例子,如果使用 BFS 进行遍历,那么节点的访问顺序是“1-2-7-8-3-6-9-12-4-5-10-11”。可以看出来 BFS 进行遍历时是一层一层的搜索的。
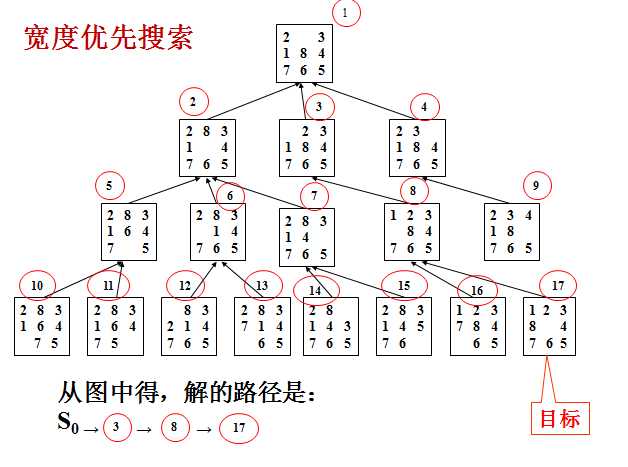
在应用 BFS 算法进行八数码问题搜索时需要 open 和 closed 两个表。首先将初始状态加入 open 队列,然后进行出队操作并放入 closed 中,对出队的状态进行扩展(所谓扩展也就是找出其上下左右移动后的状态),将扩展出的状态加入队列,然后继续循环出队-扩展-入队的操作,直到找到解为止。
上图这个例子中,红圈里的数字是遍历顺序。当找到解时一直往前找父节点即可找出求解的移动路线。
2 实验代码
```python import copy
棋盘的类,实现移动和扩展状态
class grid: def init (self,stat): self.pre=None self.target=[[1,2,3],[8,0,4],[7,6,5]] self.stat=stat self.find0() self.update() #更新深度和距离和 def update(self): self.fH() self.fG() #G是深度,也就是走的步数 def fG(self): if(self.pre!=None): self.G=self.pre.G+1 else: self.G=0 #H是和目标状态距离之和,可以用来判断是否达到最优解 def fH(self): self.H=0 for i in range(3): for j in range(3): targetX=self.target[i][j] nowP=self.findx(targetX) self.H+=abs(nowP[0]-i)+abs(nowP[1]-j) #查看当前状态 def see(self): print("depth:",self.G) for i in range(3): print(self.stat[i]) print("-"*10) #查看找到的解是如何从头移动的 def seeAns(self): ans=[] ans.append(self) p=self.pre while(p): ans.append(p) p=p.pre ans.reverse() for i in ans: i.see() #找到数字x的位置,返回其坐标 def findx(self,x): for i in range(3): if(x in self.stat[i]): j=self.stat[i].index(x) return [i,j] #找到0,也就是空白格的位置 def find0(self): self.zero=self.findx(0) #对当前状态进行所有可能的扩展,返回一个扩展状态的列表 def expand(self): i=self.zero[0] j=self.zero[1] gridList=[]
if(j==2 or j==1):
gridList.append(self.left())
if(i==2 or i==1):
gridList.append(self.up())
if(i==0 or i==1):
gridList.append(self.down())
if(j==0 or j==1):
gridList.append(self.right())
return gridList
#deepcopy多维列表的复制,防止指针赋值将原列表改变
#move只能移动行或列,即row和col必有一个为0
#对当前状态进行移动
def move(self,row,col):
newStat=copy.deepcopy(self.stat)
tmp=self.stat[self.zero[0]+row][self.zero[1]+col]
newStat[self.zero[0]][self.zero[1]]=tmp
newStat[self.zero[0]+row][self.zero[1]+col]=0
return newStat
def up(self):
return self.move(-1,0)
def down(self):
return self.move(1,0)
def left(self):
return self.move(0,-1)
def right(self):
return self.move(0,1)
计算逆序数之和
def N(nums): N=0 for i in range(len(nums)): if(nums[i]!=0): for j in range(i): if(nums[j]>nums[i]): N+=1 return N
根据逆序数之和判断所给八数码是否可解
def judge(src,target): N1=N(src) N2=N(target) if(N1%2==N2%2): return True else: return False
初始化状态
startStat=[[2,8,3],[1,0,4],[7,6,5]] g=grid(startStat) if(judge(startStat,g.target)!=True): print("所给八数码无解,请检查输入") exit(1)
visited=[] queue=[g] time=0 while(queue): time+=1 v=queue.pop(0) #判断是否找到解 if(v.H==0): print("found and times:",time,"moves:",v.G) #查看找到的解是如何从头移动的 v.seeAns() break else: #对当前状态进行扩展 visited.append(v.stat) expandStats=v.expand() for stat in expandStats: tmpG=grid(stat) tmpG.pre=v tmpG.update() if(stat not in visited): queue.append(tmpG)
```
3 实验结果
仍然用相同的例子,用 BFS 进行搜索。

将找出的解从初始状态一步一步输出到解状态。
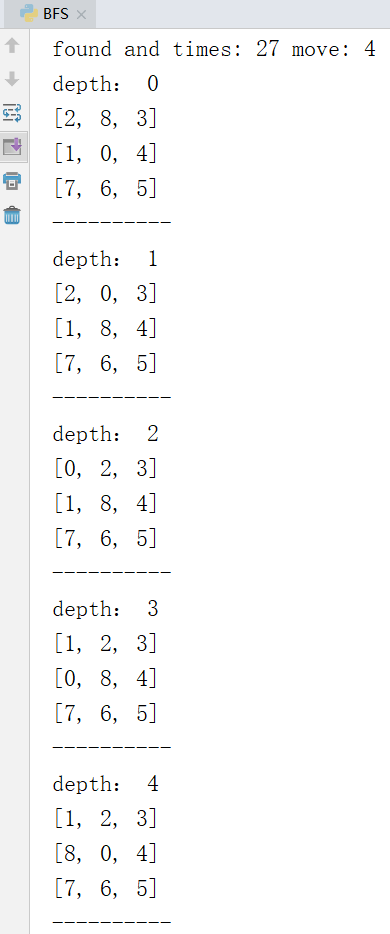
从结果中可以看出总共进行了 27 次遍历,并在第 4 层时找到了解状态。
下面我们来看一看 BFS 的所有 27 次遍历,以此来更深入的理解 BFS 的原理。稍微对代码进行改动,使其输出遍历次数和当前层数。由于结果太长,为了方便展示,下面将以树的形式展示。

上面输出的解就是按照红色路线标注找到的,从遍历次数可以看出是一层一层的找。
4 实验总结
由于 BFS 是一层一层找的,所以一定能找到解,并且是最优解。虽然能找到最优解,但它的盲目性依然是一个很大的缺点。从上面的遍历树状图中,每一层都比上一层元素更多,且是近似于指数型的增长。也就是说,深度每增加一,这一层的搜索速度就要增加很多。
参考文献
- 基于Hadoop分布式网络爬虫系统的优化研究(北京工业大学·张体)
- 主题爬虫的设计与实现(北京邮电大学·彭小明)
- 聚焦爬虫技术研究(江南大学·倪贤贵)
- 房地产信息垂直搜索引擎技术研究(杭州电子科技大学·李勇)
- 基于Hadoop分布式网络爬虫系统的优化研究(北京工业大学·张体)
- 恶意URL检测项目中基于PageRank算法的网络爬虫的设计和实现(北京邮电大学·王晓梅)
- 搜索引擎中通用爬虫系统的研究与设计(吉林大学·高龙)
- 面向垂直搜索的聚焦爬虫研究及应用(浙江大学·吕昊)
- 主题网络爬虫的研究和实现(武汉理工大学·林捷)
- 基于词嵌入的模糊文本搜索与推荐系统(东南大学·刘耘)
- 垂直搜索引擎中主题爬虫搜索策略研究与实现(沈阳建筑大学·徐晓艳)
- 基于网络爬虫的搜索引擎的设计与实现(湖北工业大学·冯丹)
- 面向特定网页的Web爬虫的设计与实现(吉林大学·马慧)
- 视频检索与推荐系统的设计与实现(华中科技大学·陈凡)
- 主题搜索引擎网络爬虫搜索策略的研究与实现(北京化工大学·夏亮)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:毕设驿站 ,原文地址:https://m.bishedaima.com/yuanma/35867.html











