PLA 感知机学习方法之Python

人工智能实验 lab3 实验报告

PLA 感知机学习方法

一、算法原理

PLA 是针对二元分类问题，它可以用来解决二维或者高维的 线性可分 问题。在二分类问题中，PLA 算法通过一个共享的权重向量$w=(w_1,w_2,...,w_d)$和某个样例的特征向量$x=(x_1,x_2,x_3...x_d)$ 做向量的内积，并通过与某个阈值$w_0$来比较大小，我们可以定义如果内积的结果大于阈值，就判为一类，反之则属于另外一类，就起到了二分类的效果。

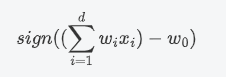
为了方便我们的算法中使用矩阵的乘法运算，也方便优化或求导，我们可以把阈值转化成一个参数融入到权重向量中：

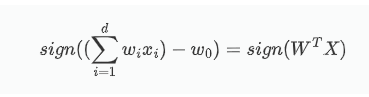
其中：

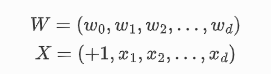
PLA 的算法步骤是：

先将权重矩阵和阈值合并，并给每一个样本特征向量前加一个 1
随机初始化一个权重矩阵
计算每个样本点的特征向量和权重矩阵的乘积，然后判断是大于 0 还是小于 0（使用符号函数 sign 来计算）。遍历所有的样本点，如果找到一个预测错误的样本，就更新权重向量，直到所有的训练样本都预测正确。如果遇到错误的样本可以通过下面的式子对权重矩阵进行更新：

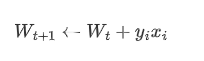
PLA 并不一定会停下来，因为如果数据存在噪声或者线性不可分的时候就会一直有错误的点，因此我们需要设置一个总的迭代次数来让算法停止。 4. 训练结束后我们会得到一个权重矩阵，我们通过这个权重矩阵和要预测的 x 做内积来预测它的标签

二、伪代码

procedure PLA_algorithm(data,w): // input: data 待训练的数据集样本点 // w 要训练的初始权重矩阵 // return: w 训练出的权重矩阵 iteration=15 for i in range(iteration): // PLA算法迭代iteration或者没有错误点的时候停止 isComplete=1 for point in data:// 遍历所有的样本点 res = point.dot(w) // 计算当前点和权重矩阵的点乘 if sign(res)=sigh(label) // 如果计算结果的符号和这个点原本的符号相同，就继续下个点 continue else: // 出现错误的点，更新权重向量w并立刻返回 w=w+label*x isComplete=False// 出现了错误的点，下次要继续迭代 if isComplete: // 如果遇到一次是没有错误点的就可以直接退出了 break return w

三、代码展示

传统 PLA 算法：

python def PLA_algorithm(data): ''' PLA算法，当算法迭代次数达到上限，或者没有错误的点的时候停止 ''' iteration=15 w = np.ones(len(data[0])) # 定义权重向量 count=0 for _ in range(iteration): # PLA算法迭代iteration或者没有错误点的时候停止 count+=1 isComplete=1 for point in data: # 遍历每个数据点不断更新w x=np.append(np.array([1]),point[:-1]) #在开头加一个1表示阈值 res = x.dot(w) if (point[-1]==1 and np.sign(res)==1) or (point[-1]==0 and np.sign(res)==-1) or res == 0: continue else: # 出现错误的点，更新权重向量w并立刻返回 w=w+(-np.sign(res))*x isComplete=False if isComplete: # 如果遇到一次是没有错误点的就可以直接退出了 break print("训练迭代了%d次"%(count)) return w

对 PLA 算法进行升级口袋算法，因为口袋算法每次迭代要更新权重矩阵 W，如果线形不可分，在遍历数据集的时候如果开头几个点一直有错误，就一直利用不到后面的数据点，所以口袋算法采用了随机选取数据点，找到错误的点进行更新的方法：

训练完成后，我们会得到一个权重矩阵 W，我们可以利用这个权重矩阵来对我们划分的验证集进行验证：

````python def k_fold(dataSet,k,i): ''' 对数据集进行训练集和验证集的划分 :param dataSet: 数据集 :param k: 划分成k个部分 :param i: 选取第i个部分为验证集 :return: 返回训练和验证集的数据 ''' total = len(dataSet) step_len=total//k # 求出每一份的长度 val_begin=i*step_len val_end=val_begin+step_len return np.vstack((dataSet[:val_begin],dataSet[val_end:])),dataSet[val_begin:val_end]

def validation(validation_set,w): count=0 total=validation_set.shape[0] for point in validation_set: # 遍历每个数据点不断更新w x=np.append(np.array([1]),point[:-1]) #在开头加一个1表示阈值 res = x.dot(w) if (point[-1]==1 and np.sign(res)==1) or (point[-1]==0 and np.sign(res)==-1) or res == 0: count+=1 print("PLA在验证集上的正确率为：%f"%(count/total)) ````

四、实验结果以及分析：

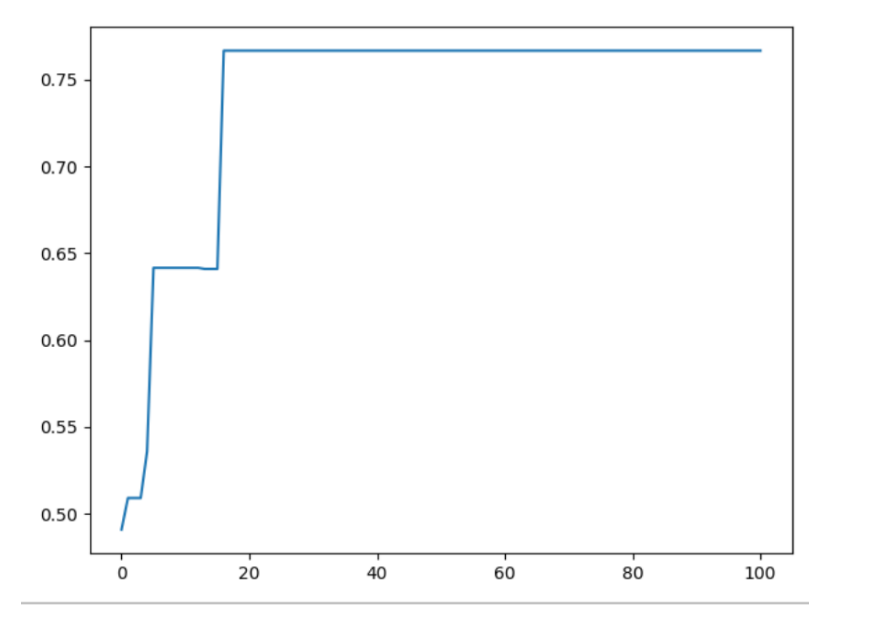
我尝试了 100 次迭代并统计每一次迭代后的在验证集上的准确率，作出的图像如下所示：

可以看到因为数据集不是线形可分的，所以 PLA 找不到一个最优的解，每次迭代更新了一次后，准确率就会波动，有可能上升也可能下降，因此可见 PLA 对于线形不可分的数据集表现并不是很出色。

再看口袋算法，每次迭代都随机选取一个点，如果是错误的就进行更正，并和当前的最好 w 进行对比，如果在训练集上表现更好，就替换原来的最好 w。可以看到，每次迭代后在验证集上的正确率一直是上升趋势，可见，口袋算法比起传统的 PLA 在非线形可分的数据集上有更好的表现效果。

五、思考题：

有什么手段可以让 PLA 适用于非线形可分的数据集：

对于非线形可分的数据集，传统 PLA 算法不会停下来，因为一直会有错误的点，如果我们仅仅是设置迭代次数让它停下来的话，我们这一次纠正了这个点，下一次纠正另外一个点的时候，有可能导致前一个点有变成错误的的点了。所以 PLA 只能保证最后是最优解，但迭代中的准确率是无法保证的。因此就有人提出了口袋算法，就是每轮迭代后，和当前口袋中放着的权重比较谁的错误率更低，我们把错误更少的放在口袋里，也就是保证口袋中的权重向量是越来越好的，这样就能得到一个相对最优解。也可以让 PLA 在线形不可分的数据集上也适用。

如果对于非线形可分的数据集，也可以采用神经网络的方法来进行分类任务。

LR 逻辑回归算法

一、算法原理

存在一些问题并不能简单的用分类问题的离散结果来表达。比如说体检的时候，人们不喜欢你分类生病还是没有生病，只希望得到一个生病的概率值。逻辑回归就是适合这种任务的模型，它的输出是连续性的条件概率值。与 PLA 类似，我们通过一个权重矩阵对样例打分，但我们不会根据这个样例是否大于或者小于一个阈值就给他分离成两个离散的类别。而是利用一个可以把加权得分映射另外一个更合理数据空间的函数：

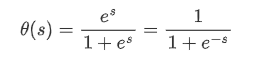
这个就是逻辑回归的函数 logistic function ，它的输入空间是正无穷到负无穷，而输出空间正好是概率的范围 [0,1] ，代入权重矩阵和样本属性可得

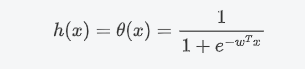
对某一个样例 x 属于某个类别 y 的条件概率我们就可以写成：

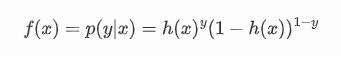
这可以作为我们的损失函数，在给定数据 x 得到 y 的概率，称为似然，考虑整个数据集的样本，我们可以得到我们的似然函数：

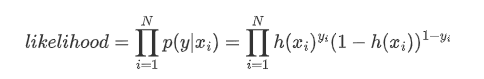
我们对上面的似然函数对目标权重向量 W 求导，化简得：

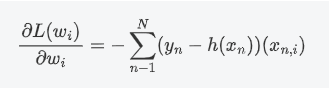
根据梯度下降法，我们可以得到权重的更新公式为：

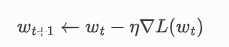
二、伪代码

procedure logistic(data,w): // input: data是逻辑回归训练数据 // w 是逻辑回归的权重矩阵 // output: w是训练完成后输出的权重矩阵 max_loop = 20 // 最大循环次数 alpha=0.1 // 设置学习率 diff = 1e-4 // 当梯度小于这个的时候停止 while max_loop>0: max_loop-=1 sum=0 //统计不同样本的计算出的梯度和 for point in data: sum+=-(point[-1]-h(w,x))*x //h(w,x)是逻辑回归的函数 w_new=w-alpha*sum // 更新权重向量 if(cal_length(w_new) <= diff): //将新的w的模长和目标最小梯度值比较，当小于后就停止迭代 break w = w_new // 将新的w赋值给旧的，开始下一轮迭代 return w

三、代码展示

基于梯度下降法的逻辑回归实现和逻辑回归函数的计算函数

````python def h(w,x): ''' 逻辑回归的预测函数h(x) ''' return 1/(1+np.exp(-(x.dot(w))))

def logistic(data): ''' 基于批梯度下降法的逻辑回归算法 ''' w=np.zeros(len(data[0])) # 定义权重向量 max_loop = 20 # 最大循环次数 alpha=0.1 # 设置学习率 diff = 1e-4 # 当梯度小于这个的时候停止 while max_loop>0: max_loop-=1 print(max_loop) sum=0 for point in data: x=np.append(np.array([1]),point[:-1]) #在开头加一个1表示阈值 sum-=(point[-1]-h(w,x)) x w_new=w-alpha sum now_diff = np.linalg.norm(w_new - w) if(now_diff <= diff): break w = w_new

return w

````

四、实验结果以及分析：

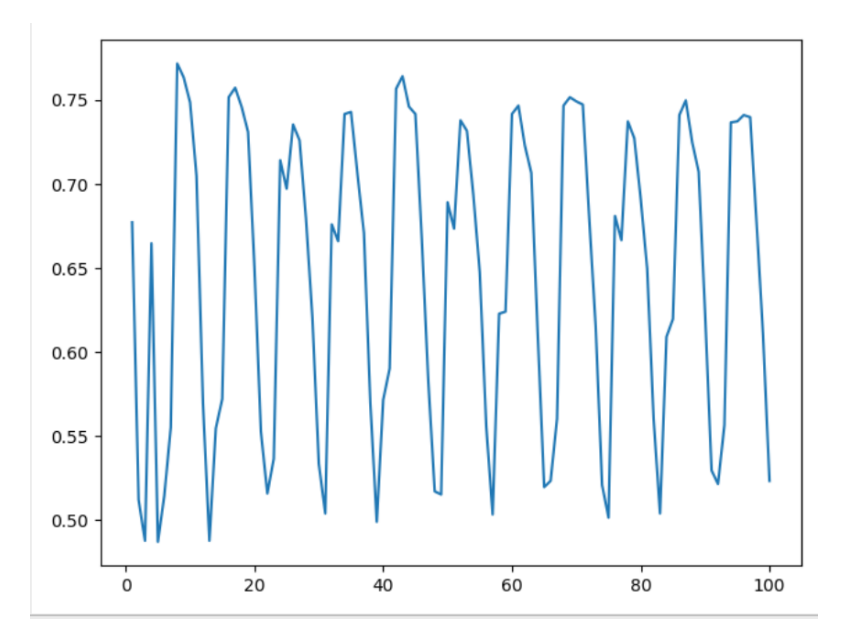
我先设置了 100 次的梯度下降次数，学习率设置为 0.01 的时候，每次迭代完都在验证集上验证一下准确度可以看到下图的实验现象，可以看到可能是因为学习率太大，导致准确度一直在最优点两侧波动，达不到最优值。如下图所示：

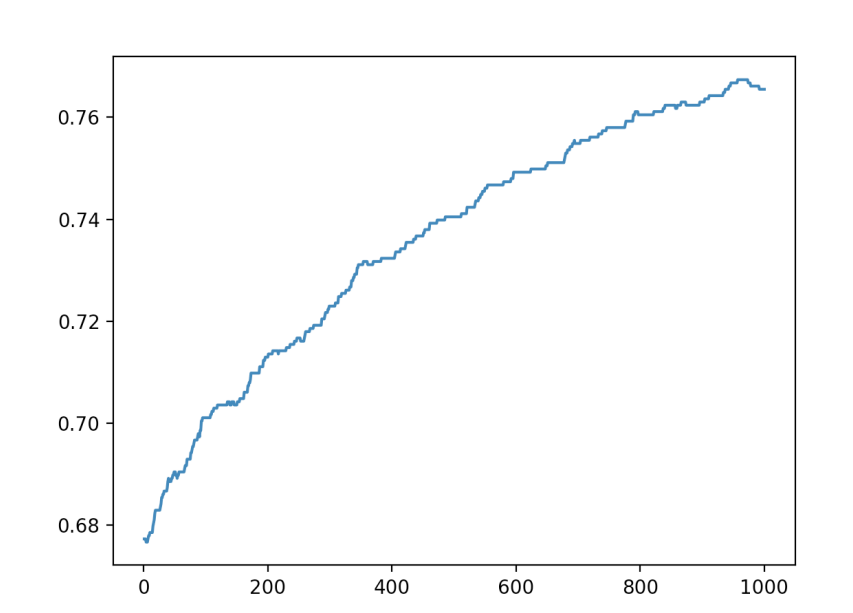
当我们把学习率调到 10 的负 7 次方后，可以看到图像总体呈现一直上升的趋势，这就符合了之前的推理，可见学习率的设置在梯度下降法中是十分重要的，要设置一个好的学习率，就需要不断的尝试不同的学习率的效果。我们可以通过记录每次的准确度变化情况，来推理学习率设置的好坏。

五、思考题

不同学习率对模型收敛有何影响，从收敛速度和是否收敛两方面来回答

学习率大可以让权重向量更新得最快，更快到达最优点。学习率小，权重向量更新慢，可能就需要更多的迭代次数来更新权重矩阵。但学习率如果太高，每次权重矩阵更新的太大，就有可能在更新的时候越过了最优点，导致在最优点附近不断震荡最后无法收敛到最优值，因此学习率的选择也十分重要。 2. 使用题目的模长是否为 0 作为梯度下降的收敛终止条件是否合适，为什么？一般如何判断模型收敛？

不合适。就那这次逻辑回归的目标函数来说，是一个严格的凸函数，但是在优化过程中，一般很难到达最优点。在最优点附近的时候梯度很低，导致变化速度越来越慢，就像对一个数一直除以 2 永远除不尽到不了 0 一样。如果学习率比较高，又有可能本来已经很接近最优值，反而越过去到了对面，因此梯度的模长为 0 作为条件不合适，最好是低于某个可以接受的模长就停止。