强化学习

“对抗 DQN 网络 Adversarial-DQN”以及 MCTS 的结合

强化学习的本质是决策，根据当前的状态来决策应该采取什么动作。跟有监督学习不同的是，有监督学习是通过已有的数据和数据对应的正确标签，学习数据和标签对应逻辑；强化学习刚开始并没有标签，它是在尝试动作后才能获得结果，通过反馈的结果信息不断调整之前的策略。若将状态看作数据属性，动作看作标签，监督学习和强化学习都是在试图寻找一个映射，从已知属性/状态推断出标签/动作，强化学习中的策略相当于有监督学习中的分类/回归器。

一、 Q-Learning

Q-Learning 是强化学习里经典的算法之一。Q-Learning 主要有 R 表和 Q 表，两个表记录的都是各个状态下各个动作的得分。

在决策时，选择 Q 表中当前状态对应的得分最高的动作作为决策。

在更新时，需要结合 R 表和当前 Q 表的信息，对 Q 表的更新是 Q-Learning 的关键，公式为：

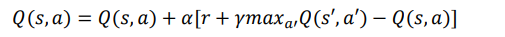
表是固定不变的，这是固定的先验知识，需要人为引入。经过多轮的迭代更新之后，Q 表就会指引 agent 以更小的代价到达 reward 值最大的状态。

二、 DQN

Q-Learning 需要的 Q 表大小为 state*action，当状态空间很大时，这个表将会变得非常大，想要构造出这么一个 Q 表几乎是不可能的事。所以后来转换了思想，Q-Learning 实际上是在寻找一个 state 到 action 的映射，因为状态空间很大，所以这个映射应该是非常复杂的，所以可以借助深度学习来拟合这个映射。

DQN 的创新点有：通过经验池解决了训练数据的相关性及非静态分布问题；使用 TargetNet 作为延迟网络，解决了稳定性问题。

引用 Nature 中的 DQN 算法伪代码：

三、 Adversarial-DQN

由于 DQN 算法设计是针对单一 agent 的，所以在连续的不同状态下，都是这一个 agent 执行动作，即连续的两个状态下 agent 的目标都是一样的最大化 reward 值，所以更新公式为：

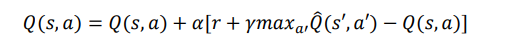
但是现在的情景是下棋，是双方的博弈，这样相当于有两个 agent，对于他们各自而言目标都是最大化自己的 reward，这样就会相应的减小对方的 reward。而且，连续两个状态下动作的执行者是不同的，这样存在 agent 的切换的情形不同于 DQN，所以我们提出了一种新的模型：Adversarial-DQN。

该模型由两个 DQN 组成，分别对应于 1，2，并且训练时的经验池只记录属于自己的经验，即(s,a,r,s_)，s∈。在训练时，由于状态 s 对应的后继状态 s_是属于对方的，所以当前值网络的更新公式修改为：

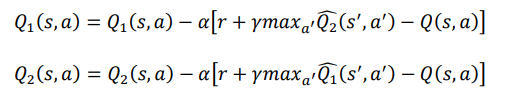
其中 1、1、2、2 分别对应于两个 DQN 网络的当前值网络和目标值网络。

对 1 进行更新时，我们把后继状态′输入对方的目标值网络，而不像 DQN 那样输入到自身的目标值网络。而且因为对方的 DQN 网络的目标也是最大化自身的 reward，所以对方的目标值网络 2 输出的是对方的最大值得分，所以在更新自己

的网络时应该是减去对方的网络输出。

A-DQN 结构如下：

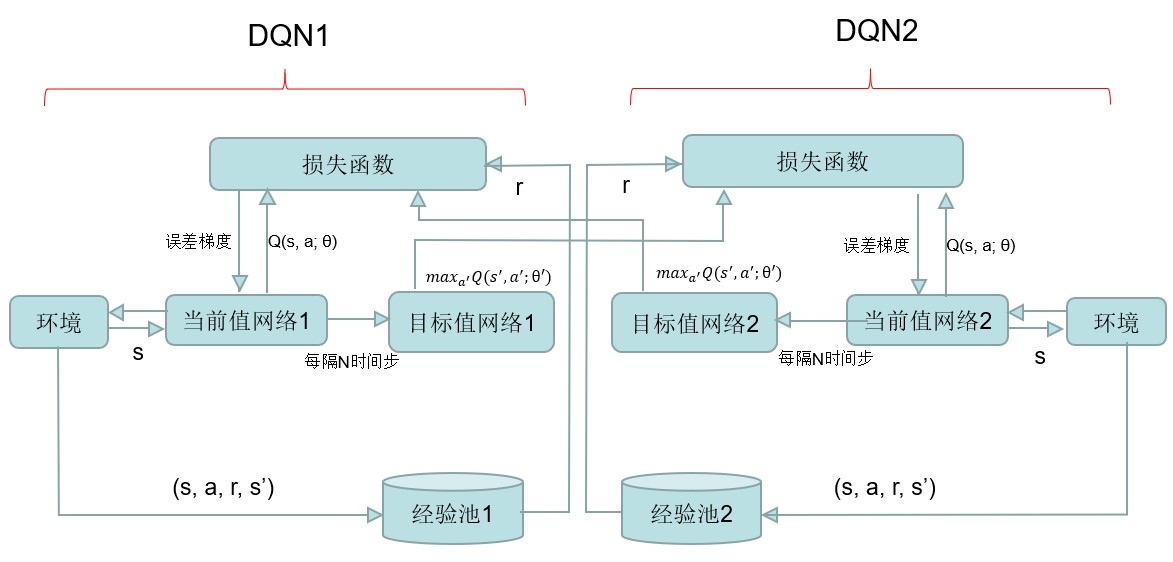
训练时在 episode 中同时更新 DQN1 和 DQN2，分别在各自的经验池中随机抽选 minibatch 个样例，为了使梯度更新更加充分，在一个 episode 里还要反复训练 n 次，每一次都重新对经验池进行随机抽样。

DQN 网络结构因为棋盘大小是 8 8，而状态 state 表示的就是当前棋盘的局面，所以可以用 1 64 大小的向量表示状态，对应位置上为 1 代表黑棋，为-1 代表白棋，为 0 代表空。而动作可以表示为在落子在棋盘的某个位置，所以也可以用一个 1 64 大小的向量表示 action，但考虑到有可能当前状态下没有位置可以走，所以增加一个表示跳过的 action，即表示为 1 65 大小的向量。

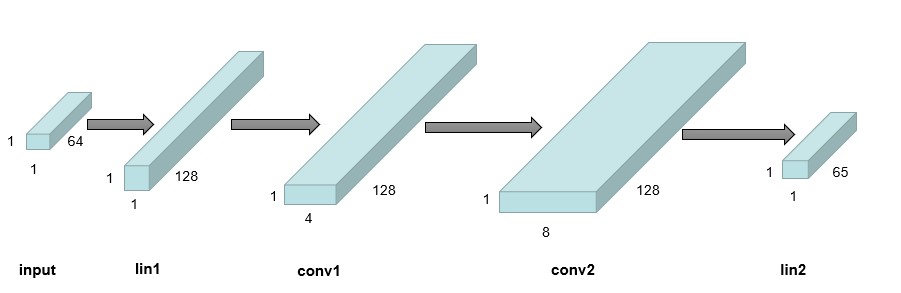
所以我们可以设计网络输入为 1 64 维的 tensor，输出为 1 65 维的 tensor，输出表示各个 action 的得分，在合法位置集合中挑选得分最高的 action 就是网络预测的决策。网络结构图如下：

自博弈构造经验池数据

强化学习归根结底还是数据驱动的方法，所以想要训练出一个好的模型的话需要大量的数据。DQN 一个优点就是可以通过自博弈自动构造训练数据，我们只需要人工地加入 reward 值、或评价值即可。

游戏的初始状态是棋盘上共有 4 个棋，黑白各两个。游戏规定黑棋先手，所以把这个初始状态输入到 DQN1，网络输出一个动作 action，并且游戏状态相应地转变为 s’。现在还差这一步的 reward 值，如果我们引入评价函数，就可以根据当前棋盘上的局面评价出这一步的得分，但是因为我们对黑白棋游戏并不熟悉，而且这个游戏比之前的五子棋复杂得多，所以不可能设计出一个合理的评价函数。如果评价函数设计得不好，反而会引入了错误的先验知识，这样反而会使得模型效果变差。所以我们的方法是，如果这一步使得游戏结束了，若是己方胜利则该步的 reward 值为 100，若是对方胜利则该步的 reward 值为-100，其余情况下 reward 值都为 0。这样设计 reward 值会存在反馈延迟的问题，这一步得到的经验需要在很久以后才能学习到它的反馈，相当于训练数据效率较低。但是如果数据足够多，训练时间足够的话，模型还是可以学习到这些数据的知识慢慢收敛的。

这样我们就构造完成了经验池中的数据，如前面所说的，如前面 A-DQN 中描述的，一个 DQN 的经验池只记录属于自己的数据，即(s,a,r,s_)，s∈agent。

蒙特卡罗树搜索：

在上一次实验的五子棋设计中，我们通过设计评价函数和使用博弈树的搜索方法来选择下一步的落子，取得了很好的效果，不过在五子棋中，我们就算使用了 alpha-beta 剪枝优化，下一步也有一定的延迟，而在本次实验的黑白棋中，我们自身对黑白棋就很不熟悉，自然很难去设计一个比较好的对当前棋局的评价函数，只能一直模拟对弈到棋局结束，再根据胜负回溯结果，不像五子棋的博弈树搜索可以限制搜索深度。如果每一步都这样搜索，解空间就会非常的大，落子速度非常的慢，没有实际的应用价值。

因此我们采用了蒙特卡罗 MCTS 的搜索方法，它本质上还是一种搜索的算法。对于黑白棋，MCTS 沿着博弈树不断的往下模拟，一直到叶子节点，也就是棋局无处可以落子，或者某一方被吃光，然后胜者评分为 +1，负者评分为-1，然后通过回溯的方法将棋局的结果信息一直往上传播，直到起始节点。反复进行多次模拟搜索，当搜索结束时（受限于时间或计算能力），就可以根据已经收集的统计信息来决定下一步怎么走。

MCTS 和传统的博弈树搜索的区别就在于，博弈树搜索对当前棋局决定落子，

需要把它的所有子节点的得分统计出来然后作出决定，但 MCTS 因为没有评价函数，只能直接模拟到棋局结束，尽量多的模拟这些搜索线路，相当于对完整的棋局采样，最后通过采样的结果得出结论。可以看出如果时间和计算能力充足，使用传统博弈树搜索是可以达到最优解的，但 MCTS 是采样的过程，所以采样数量再大也只能接近最优，但可能这一点准确度换来的是很大的时间开销的节省，因此在一般的对局中，如果没有设计的很完美的评价函数，我们可以用 MCTS 来加快落子速度。

MCTS 需要模拟落子，但下棋的时候落子的选择有很多，如果我们落了一些没意义的点，就浪费了时间开销。因此我们要尽量选择一些好的落子位置，我们决策落子是依靠一个 rollout policy 函数：

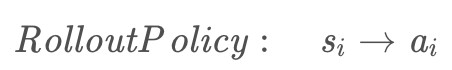
这个函数的输出结果告诉我们要选择的落子位置。传统的决策函数，比如说 UCT 就广泛应用于棋类游戏中：

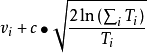
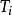
式中：

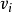
是以节点

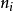
为根节点的子树的所有仿真结果的平均值，反映了根据目前仿真结果观测到的节点

能提供的回报值的期。是节点

的访问次数，也是节点

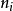
树内选择策略选中的次数。

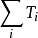
是节点 n 的访问次数。c 是一个手工设定的常数。 c 的作用是平衡 UCT 算法的利用需求（exploitation）和探索需求

exploration）。

在我们本次实验中我们使用了训练的 DQN 网络来作为 rollout 函数辅助 MCTS 搜索。使用 E-greedy 策略。当然我们也可以给模拟一个随机性也就是贪婪策略，有一定几率不接受 rollout 函数的选择的落子位置，而是选择其他的节点，否则就遵从 DQN 的输出结果模拟。当模拟了一些数据后，我们就可以用这些数据去 DQN 中用 q-learning 的更新公式更新的我们的 DQN 网络，然后再将 DQN 应用于模拟 MCTS 上，如此反复，实现了一个不断自我对弈提升下棋水平的强化学习模型。

有了 MCTS 的模拟策略函数，我们就可以进行模拟棋局并回溯棋局结果进而更新我们的策略网络或策略公式。MCTS 搜索分为四步：

选择：

在选择阶段，需要从根节点，也就是要做决策的局面 R 出发向下选择出一个最急迫需要被拓展的节点 N，局面 R 是是每一次迭代中第一个被检查的节点；

对于被检查的局面而言，他可能有三种可能： o 该节点所有可行动作都已经被拓展过

该节点有可行动作还未被拓展过 o 这个节点游戏已经结束了对于这三种可能：

如果所有可行动作都已经被拓展过了，那么我们将使用 UCB 公式计算该节点所有子节点的 UCB 值，并找到值最大的一个子节点继续检查。反复向下迭代。

如果被检查的局面依然存在没有被拓展的子节点(例如说某节点有 20

个可行动作，但是在搜索树中才创建了 19 个子节点)，那么我们认为这个节点就是本次迭代的的目标节点 N，并找出 N 还未被拓展的动作 A。

创建并拓展此结点

如果被检查到的节点是一个游戏已经结束的节点。那么从该节点直接反向传播

拓展：

树一开始是空的，是在不断的拓展下，建立新的结点

在选择阶段结束时候，我们查找到了一个最迫切被拓展的节点 N，以及他一个尚未拓展的动作 A。在搜索树中创建一个新的节点 Nn 作为 N 的一个新子节点。Nn 的局面就是节点 N 在执行了动作 A 之后的局面。

模拟：
为了让 Nn 得到一个初始的评分。我们从 Nn 开始，让游戏随机进行，直到得到一个游戏结局，这个结局将作为 Nn 的初始评分。一般使用胜利/失败来作为评分，只有 1 或者 0。
反向传播：

在 Nn 的模拟结束之后，它的父节点 N 以及从根节点到 N 的路径上的所有节点都会根据本次模拟的结果来添加自己的累计评分。如果在选择阶段中直接发现了一个游戏结局的话，根据该结局来更新评分。

每一次迭代都会拓展搜索树，随着迭代次数的增加，搜索树的规模也不断增加。当到了一定的迭代次数或者时间之后结束，选择根节点下最好的子节点作为本次决策的结果。

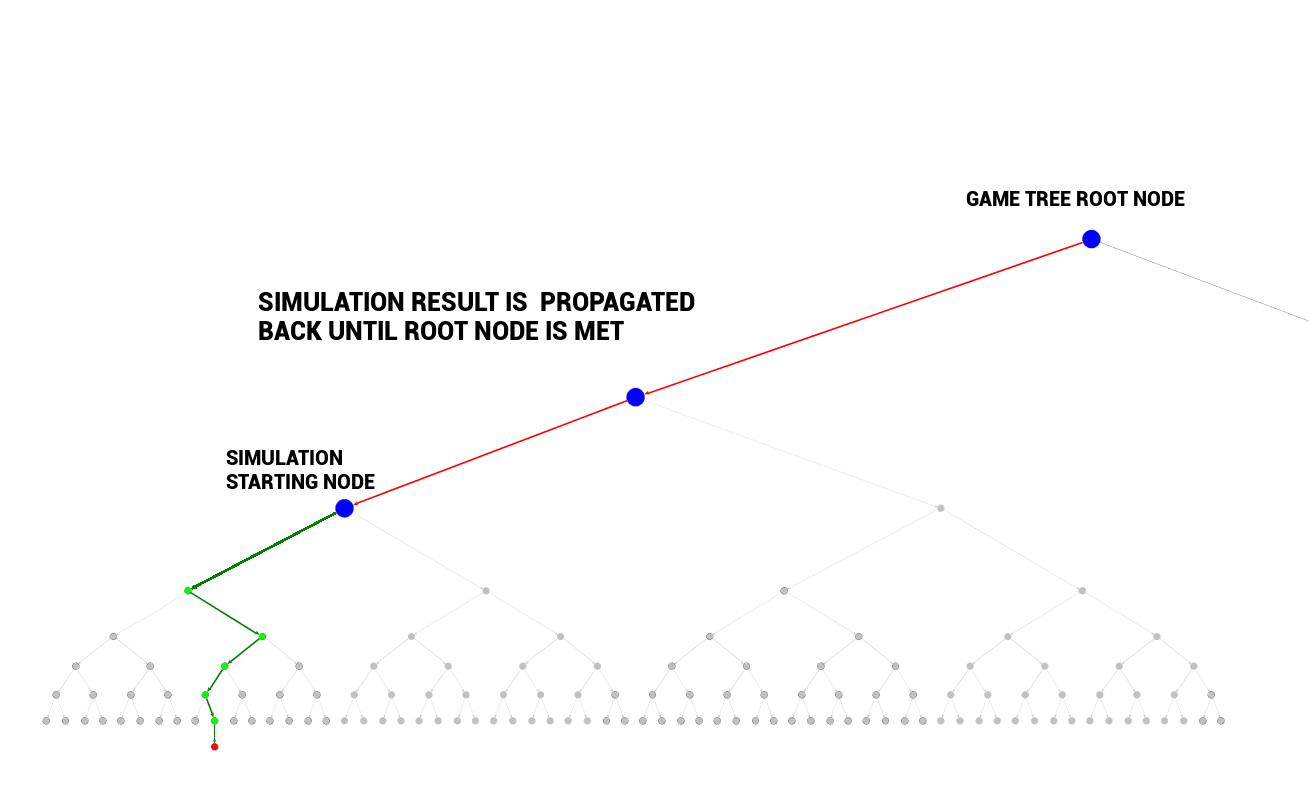
通过 MCTS 模拟自我对弈的过程，我们就可以一直更新我们的网络，因为棋

类游戏的棋盘比较大，所以解空间很大，使用 MCTS 模拟然后更新策略网络需要训练很久，如果训练时间不够长，或者网络拟合的能力不行，DQN 网络的输出结果如果直接用来对弈往往取得的效果不是特别好，因此在真正对弈的时候，我们可以再将 MCTS 网络和 DQN 网络做一个结合，使用 MCTS 在 DQN 网络的指导下进行一定数量的对局，然后用传统的 UCT 或者其他的函数来选择。或者我们可以用

MiniMax 的搜索策略，往下搜索一定的深度，用 DQN 网络对棋局评分然后回溯，选择收益最大的一个结点落子。

使用评价函数的搜索：

在第一周的对弈中，我们取得了 5 胜 1 负的战绩，可能因为训练时间比较长，取得了不错的成绩。输的那一局和对方讨教后，才知道对方是模仿上次五子棋的写法，使用了评价函数加 MiniMax 的搜索策略和一些 Q-learning，使用了网上学来的人类专家制定的评价棋局的策略，再加上搜索的算法，可以实现一个很快速的落子，并且战绩不俗。经过网上的学习发现，黑白棋的评价函数设计是有一定困难的，四个角落的落子会给比较高的分数，因为他们不会被翻转，而中间的往往分数会比较低，基于给落子评分的思想，网上有一些十分复杂的评价函数的实现，如果能对当前棋局评价，我们可以大幅度缩小搜索的范围和深度，有效且快速的落子，确实是一个很好的办法。

不过，我们个人对黑白棋本身也不熟悉，更不可能去自己设计一个复杂的评价函数，所以终究是使用了别人的经验策略，此时 Q-learning 的意义就不是特别的大，也没有体现强化学习的特点，这些评价函数的框架往往是写好的，可能会存在一些对这些参数的训练过程，但受限于框架的参数数量和框架的能力限制，可能在算力较差的环境下才可能取得比较好的效果，面对大量数据训练的强化学习模型，很容易就被击败。而且这种模型往往需要有经验的人设定得分评价方法，就没有体现到人工智能的自我学习游戏规则不断进步的特点，而强化学习则是从零开始，依靠不断的自我博弈，只知道简单的落子规则和最终是哪一方获胜，通过反复学习训练，最终取得了比较好的效果。

实现过程

定义网络结构

```python class NET(nn.Module): """定义网络结构

    Returns:
    x [tensor] -- (batch, N_ACTION)，每一行表示各个action的分数
    """         def __init__(self):
    super(NET, self).__init__()         self.linear1 = nn.Sequential(             nn.Linear(N_STATE, 128),             nn.LeakyReLU()
                                                                    )         self.conv1 = nn.Sequential(             nn.Conv1d(1, 4, 3, 1, 1),             nn.LeakyReLU(inplace=True)
                                                                                                        )         self.conv2 = nn.Sequential(
        nn.Conv1d(4, 8, 3, 1, 1),             nn.LeakyReLU()

self.linear2 = nn.Sequential( nn.Linear(8*128, N_ACTION) ) ```

如前文所述，网络的输入是当前棋盘的状态，即可以表示为一个 1 64 的 tensor，然后经过几个全连接层和卷积层，最后的输出是 1 65 维的 tensor，反映的是各

种 action 的得分。

四、ε-greedy 算法选择 action

```python def Choose_Action_EpsilonGreedy(self, x, game_state, color, Epsilon=0.1): if color == 1: avaliable_pos = game_state.Get_Valid_Pos(game_state.black_chess, game_s tate.white_chess) elif color == -1: avaliable_pos = game_state.Get_Valid_Pos(game_state.white_chess, game_s tate.black_chess)

                            avaliable_pos = list(map(lambda a: game_state.board_size*a[0]+a[1], avaliab le_pos))   # 列表,表明合法位置         if len(avaliable_pos) == 0:
                                                return 64               # 表示这一步只能跳过

                                            if np.random.uniform() < Epsilon:

rando m choose an action

                                                            action = np.random.choice(avaliable_pos, 1)[0]
                                                    else:

choos e the max Q-value action

                                                                        x = torch.tensor(x, dtype=torch.float)             x = x.view(1,-1)
                                                                                actions_values = self.Q(x)[0]      # 65维tensor，各个action在各个位置的值

                                                                                        ava_actions = torch.tensor(actions_values[avaliable_pos])
                                                                                                _, action_ind = torch.max(ava_actions, 0)             action = avaliable_pos[action_ind]         return action

```

ε-greedy 算法选择 action，以 ε 概率随机选择一个动作，否则就按网络的输出

结果来选择最优动作。结合黑白棋游戏时，因为每一步的合法动作是有限的，所以随机选择动作只能在合法动作集合里选择，根据网络输出选择最优动作也是在合法动作集合里选择得分最大的动作。因为 ε-greedy 算法保留了一定几率的随机动作，所以一定程度上削弱了网络对游戏状态的控制，让网络的输出有一定概

率去探索新的局面，避免了因为训练数据的不全面、不充分而造成过拟合。

更新网络参数

```c++ def Learn(self, oppo_Q_): for step in range(10): if self.learn_iter % UPDATE_DELAY == 0:

u pdate parameters of Q_ 每隔一段时间将Q的参数直接给到Q_

    self.Q_.load_state_dict(self.Q.state_dict())             self.learn_iter += 1

                sample_index = np.random.choice(TRANSITIONS_CAPACITY, BATCH_SIZE)   # r andomly choose BATCH_SIZE samples to learn 从经验池中随机选取进行训练             batch_tran = self.transitions[sample_index, :]             batch_s = batch_tran[:, :N_STATE]
                               batch_a = batch_tran[:, N_STATE : N_STATE+1]             batch_r = batch_tran[:, N_STATE+1 : N_STATE+2]             batch_s_ = batch_tran[:, N_STATE+2:]

                                         batch_s = torch.tensor(batch_s, dtype=torch.float)             batch_s_ = torch.tensor(batch_s_, dtype=torch.float)             batch_a = torch.tensor(batch_a, dtype=int)             batch_r = torch.tensor(batch_r, dtype=torch.float)

                                                 batch_y = self.Q(batch_s).gather(1, batch_a)                        # g ather figure out which action actually is chosen 相当于从第一维取第batch_a位置的值             batch_y_ = oppo_Q_(batch_s_).detach()                               # d etach return a new Variable which do not have gradient detach就是禁止梯度更新，这些图变量包含了梯度，在计算loss的时候会更新，因为Q_不用更新，因此禁止梯度。
                                                             batch_y_ = batch_r - GAMMA * torch.max(batch_y_, 1)[0].view(-1,1)   # m ax(1) return (value,index) for each row

                                                                     loss = self.criteria(batch_y, batch_y_)             self.optimizer.zero_grad()             loss.backward()             self.optimizer.step()

```

每次训练时从经验池中挑选 minibantch 训练样本，用这些样本得到的梯度来更新网络。而且 DQN 有两个网络，一个是当前值网络 Q，另一个是预测值网络 Q_，网络 Q_作为一个延时网络，解决了 DQN 不稳定的问题。每当 Q 网络更新一定次数后，把 Q 网络的参数复制给 Q_网络，其他时候 Q_网络不需要进行更新。

要注意的是，如前文所述我们提出的 A-DQN 模型，在计算误差 loss 时使用的是对方的 Q_网络的输出，所以这个函数接受一个参数是对方的 Q_网络，把后继状态 s_输入对方的 Q_网络得到的输出与自身网络的输出做一个均方误差，用这个误差来反向传播更新参数。

自博弈构造数据

在一个世代里，先创建一个游戏对象，然后双后逐步地进行落子模拟博弈，双方模拟落子的策略就是来源于 DQN 的输出：

```c++ = game_state.Get_State() a = offensive.Choose_Action_EpsilonGreedy(s, game_state, 1) game_state.Add(1, a) r = game_state.Gameover() * 100.0 s_ = game_state.Get_State() offensive.Store_transition(s, a, r, s_)

                             if r != 0 or round_ > 100:

当这局游戏结束或双方下够了100次。经验池已经有很多样本，此时可以开始训练

                             offensive.Learn(defensive.Q_) defensive.Learn(offensive.Q_) print('Episode:{} | Reward:{}'.format(episode, r)) break

```

因为我们的 A-DQN 模型是分开先手、后手两个单独的模型的，所以对先手的模型而言，只记录属于自己的记录到经验池。上述代码中，s 表示当前状态；a 表示由 DQN 网络输出的动作；r 表示 reward 值，如果游戏结束了为 100 或-100，否则为 0；s_为后继状态。

对于后手的模型也是同理构造数据，一旦 r 不为 0 的话，代表这一次的模拟已经结束了，所以就开始对两个模型进行参数更新。

五、MCTS

蒙特卡洛树较为关键的一点是“拓展”和“反向传播”，当一个叶节点不是终止状态时，就要对这个节点进行拓展，一直到终止状态，然后对节点的值进行反向传播。

```python def expand(self, action_priors): for action, prob in action_priors: if action not in self._children: self._children[action] = TreeNode(self, prob) def update(self, leaf_value): """Update node values from leaf evaluation. """

Count visit.

                                 self._n_visits += 1

Update Q, a running average of values for all visits. self._Q += 1.0*(leaf_value - self._Q) / self._n_visits

                                         def update_recursive(self, leaf_value):

If it is not root, this node's parent should be updated first if self._parent:

                                         self._parent.update_recursive(-leaf_value)     self.update(leaf_value)

```

在选择节点时，可以用 UCT 公式，但是因为我们现在有 DQN 模型，所以可以把

DQN 模型融入到节点选择上，根据网络的输出值来选择节点。

实验结果

因为得到的模型无法像有监督学习里的分类任务那样有明确的指标衡量，所以只能通过实战来粗略地验证模型的效果，下面使用训练好的模型和网上的黑白棋小游戏进行博弈作为验证。我们的模型执黑子，对方执白子。

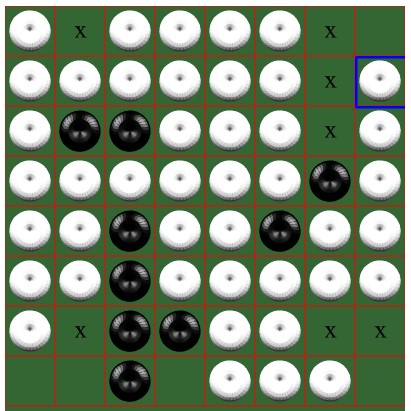
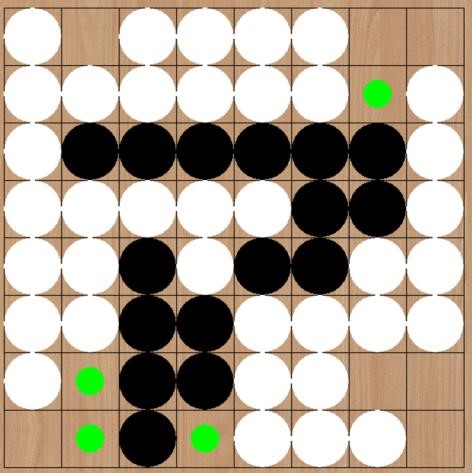
游戏某个状态如左图，这时白棋刚刚走完，轮到己方模型落子。可以见到模型选择了(0,3)位置落子，因为我们的模型并没有设计评价函数，而是完全通过大量数据训练出来的模型，所以单独对每一步的可解释性较差。因为这个游戏主要讲究占据位置，所以边角位置是最优先的选择。这一步有许多边角位置可选，

大概是因为在这一个位置可以造成有两个方向上的交叠，所以对己方局势更有利。

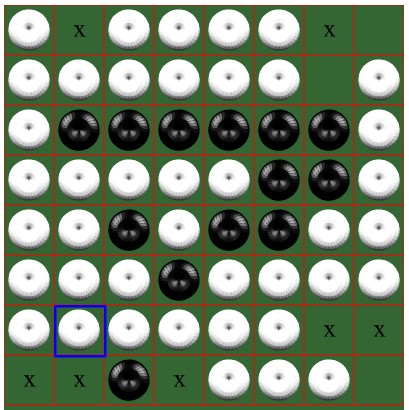
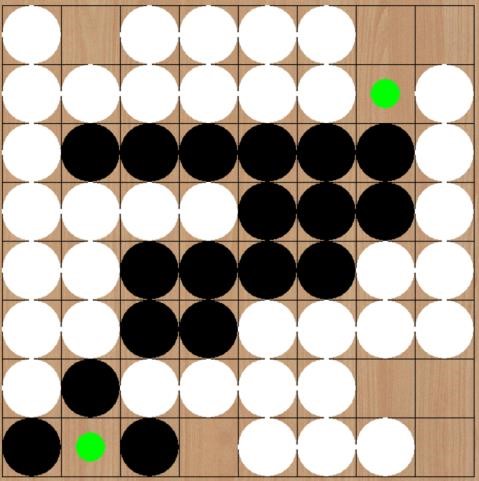
后来游戏某个状态如左图，这时白棋刚刚走完，轮到己方模型落子。可以见到模型选择了(2,6)位置落子。这时模型并没有绝对地选择边角位置进行落子，而是选择了一个连通了三个方向的位置。可能的原因是这时候可以选择的边角位置都仅仅连通一个方向，并且很有可能会因为落子在那些位置反而让对方去占领四个角落之一，这是最得不偿失的。所以模型判断这时候最有利的位置并不是边界上的。

后来游戏某个状态如左图，这时白棋刚刚走完，轮到己方模型落子。可以见到模型选择了(7,0)位置落子。因为四个角落的位置是不会被对方吃掉的，所以这个位置应该是最优先去争夺的。所以当合法位置有四个角落时，都应该最优先考虑它。

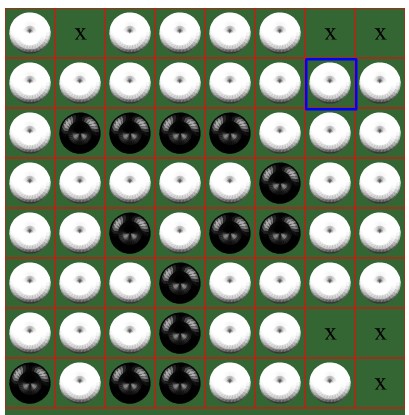
后来游戏某个状态如左图，这时白棋刚刚走完，轮到己方模型落子。模型选择了(7,7)这个角落位置，这符合上一步中的分析，模型优先抢占了角落位置。之后轮到白子走，但是白子这时并没有可以走的位置，所以继续是黑子，这时模型选择了(6,7)这个位置，使得己方的黑棋慢慢从边界处向中间包围过去。并且这一步还防止了对方占领其余的边界位置，所以是对己方最优的。

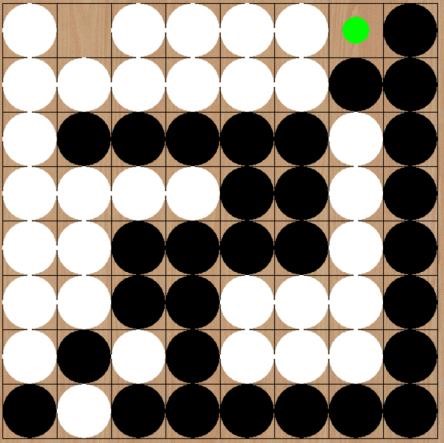
之后轮到白棋走，白棋只有一个位置能下，所以如左图。然后我们的模型又选择了右上角的位置(0,7)，这时游戏基本就结束了，我们的模型取胜了。

上面过程就验证了我们训练好的模型的确能选择己方优势的动作，在上一周的小组比赛中，我们的模型也是取得了 5 胜 1 负不错的成绩，因为我们的模型使用了 DQN 的输出来简化 MCTS，所以下子速度会比较快，而且因为训练了一定的时间，所以在正确性上也有一定的保证。在输了的一局中，我们和对方讨论了实现的方法、细节，原来对方是加入了较为专业的评价函数，这一点确实是比我们的模型要好的，因为黑白棋不像围棋那么复杂，所以设计一个全面、合理的评价函数是完全有可能的，如果有这么一个非常准确的评价函数，那么在训练、搜索时确实是比我们的模型要更高效、更准确。