一、理论知识

1.1 K-Means

给定一组数据集，聚类算法将它们分成不同的子组。我们希望类内实例高度相似，类间实例低相似。

在样本集中，随机选取K个点作为中心$\bold \mu_k$，计算每个样本到中心点的距离，并将样本划分到离它最近的那个点的集群中。使用变量$r_{nk}$表示数据样本$\bold x^{(n)}$是否属于集群k： $$ r_{nk}=\left{\begin{matrix}1,k=arg\min_j||\bold x^{(n)}-\mu_j||^2\0,otherwise\end{matrix}\right. $$ 对于每个集群，用所有样本的平均位置更新中心点的位置： $$ \mu_k=\frac{\sum^N_{n=1}r_{nk}\bold x_n}{\sum^N_{n=1}r_{nk}} $$ 重复上面的样本分配和中心更新过程即可，该过程是保证收敛的。类内距离之和会随着K的增大而减小，因此选择K的时候考虑寻找使得距离基本收敛的K值或是依据下游应用需求选择K值。

K平均聚类的结果高度依赖于初始化的中心点。选择初始化中心点的一般方法有：

随机选择：随机选择数据样本作为初始中心。问题在于有可能选择了距离很近的多个样本作为初始中心
基于距离的方法：一开始随机选一个样本作为中心点，其他时候选择离各个中心最远的样本作为中心点。问题在于可能选到异常值
随机+距离方法：第一个中心点为随机选择的样本，从全部远离现有中心的样本中随机选择下一个中心

一个点要么属于一个集群，要么不属于，存在赋值难的问题。可以用软K平均算法解决： $$ r_{nk}=\frac{e^{-\beta}||\bold x^{(n)}-\mu_k||^2}{\sum^K_{i=1}e^{-\beta}||\bold x^{(n)}-\mu_i||^2} $$ 这样一来，$r_{nk}$可以理解为样本属于某个集群的几率。

该算法还对异常值敏感。而且欧几里得距离决定了决策边界是球形的，当不同簇的形状不规则时，性能可能不佳。

1.2 GMM与EM算法

在监督学习中，回归和分类都可以理解为学习的条件概率分布。类似地，从概率建模的角度来看，无监督学习可以理解为对输入数据的概率分布进行学习，最简单的方法是假设该分布为高斯形式。但是一般情况下，样本的分布比高斯分布复杂得多。为了更好地建模，就需要更好的分布表示方法，即使用复杂的分布，但是训练成本又会增加。

因此，一个直观的思路是使用很多简单模型的加和表示复杂模型： $$ p(\bold x)=\pi_1p_1(\bold x)+\pi_Kp_K(\bold x) $$ 其中，所有$\pi$的和为1，用来使得分布合法。而每个$p_i$表示简单的分布。上面的每一项又可以看作是联合分布的边缘分布： $$ p_z(\bold x)\pi_z=p(\bold x|z)p(z)=p(\bold x,z) $$ 这种模型被称为潜变量模型LVM。我们将各个分布看做是高斯分布，则该模型又称为高斯混合模型，即GMM。如果一个高斯混合模型由$K$个高斯分布组成，则总的分布表达式为： $$ p(\bold x)=\sum^K_{k=1}\pi_kN(\bold x;\bold\mu_k,\bold\Sigma_k) $$ 其中，$K$表示高斯分布的个数，$\pi_k$表示第$k$个分布的权重。$\sum^K_{k=1}\pi_k=1$。$\bold \mu_k$和$\bold \Sigma_k$是第$k$个高斯分布的均值向量和协方差矩阵。

EM算法可以学习高斯混合模型的参数，使得该模型在特定的数据集下获得更大的对数似然函数值。算法分为E和M两步。E指评估预期，M指更新数据：

E-step：$Q(\bold\theta;\bold\theta^{(t)})=E_{p(\bold z|\bold x;\bold\theta^{(t)})}[\log p(\bold x,\bold z;\bold \theta)]$
M-step：$\bold\theta^{(t+1)}=\arg\max_\bold\theta Q(\bold \theta;\bold\theta^{(t)})$

对于上述的高斯混合模型，在E-step中，可以求得对数似然函数为： $$ \log p(\bold x,\bold z;\bold \theta)=\sum^K_{k=1}z_k\cdot[\log N(\bold x_n|\bold \mu_k,\bold\Sigma_k)+\log\pi_k] $$ 令： $$ \gamma_k^{(t)}\triangleq\frac{N(\bold x_n|\bold \mu^{(t)} k,\bold\Sigma^{(t)}_k)\pi_k}{\sum {i=1}^KN(\bold x_n|\bold \mu^{(t)} k,\bold\Sigma^{(t)}_k)\pi_i} $$ 则有： $$ Q(\bold\theta;\bold\theta^{(t)})=\sum {k=1}^K\gamma_k^{(t)}[\log N(\bold x_n|\bold \mu_k,\bold\Sigma_k)+\log\pi_k] $$ 然后在M-step更新各个参数： $$ \bold\mu_k^{(t+1)}=\frac1{N_k}\sum^N_{n=1}\gamma_{nk}\bold x_n\ \bold\Sigma_l^{(t+1)}=\frac1{N_k}\sum^N_{n=1}\gamma_{nk}(\bold x_n-\mu_n^{(t+1)})(\bold x_n-\mu_n^{(t+1)})^T \pi_k^{(t+1)}=\frac{N_k}N $$ 其中$N_k=\sum^N_{n=1}\gamma_{nk}$，表示第$k$类的样本的有效数量。反复执行E和M两步训练参数，直至模型收敛或到达最大训练次数即可。

二、代码实现

2.1 K-means

在K-means算法中，我们将训练数据集分成若干个聚类，对每个类打上标签后对训练样本进行分类，将属于的类的标签当做预测结果即可。

2.1.1 中心点的选择

K平均算法的核心就是中心点的选择和更新。对于本次实验使用的MNIST数据集，样本共有10类，因此聚类时选择10个不同的中心点。初始化中心点有多种方法，我会在之后的实验结果分析中分析不同的初始化方法对结果的影响。

下面的代码以随机选择为例子。在全部样本点中选择十个样本点作为初始化中心：

```python

设置基本参数

k = 10 # 类别数 t = 100 # 迭代次数

生成初始中心

完全随机

center_points = np.random.choice(train_images.shape[0], k, replace = False).tolist() for i in range(len(center_points)): center_points[i] = train_images[center_points[i]] center_points = np.asarray(center_points) ```

同时，我还对基于距离的方法进行了尝试。即，第一个中心点为随机选择的样本点，第二个中心点为离第一个中心点最远的样本点，第三个中心点为距离第一和第二个中心点距离之和最大的样本点，以此类推：

python center_points = genCenterPoints(train_images, k)

```python

基于距离选择中心点

def genCenterPoints(train_images, k): # 第一个中心点随机选择 center_points = [train_images[random.randint(0,train_images.shape[0]-1)].tolist()] while len(center_points) != k: print(len(center_points)) dist = None point = None # 遍历每个样本点 for each in train_images: # 不考虑已经作为中心点的样本点 if each.tolist() in center_points: continue # 计算当前样本到各个中心点的距离之和 tmp_dist = np.sum(np.linalg.norm(np.asarray(center_points) - each,axis = 1)) # 选择距离最短的样本点作为下一个中心点 if dist==None or tmp_dist<dist: point = each dist = tmp_dist center_points.append(point.tolist()) return np.asarray(center_points) ```

2.1.2 训练过程

之后就是对各个样本点进行分类和中心点的迭代更新：

```python

进行迭代

for i in range(t): # 对训练样本进行分类 r = classification(center_points,train_images, k) # 更新中心点位置 center_points = updateCenterPoints(r, train_images, k) ```

对样本点进行分类时，使用数组 r[i][j] 表示第 i 个样本是否属于第 j 类。是则为1，否则为0。计算出当前样本和各个中心点之间的距离，选择最近的中心点作为该样本属于的类别即可。这里我调用了 np.linalg.norm 来计算距离，得到的是欧式距离，也就是各个特征值的平方和开根号作为距离。样本距离可以采用不同的标准，会对分类的结果产生不同的影响。

python def classification(center_points,train_images, k): # r[i][j]表示第i个样本是(1)否(0)属于第j类 r = np.zeros((train_images.shape[0],k)).astype(np.int16) for i in range(train_images.shape[0]): # 计算样本距离各个中心点的距离 distance = np.linalg.norm(center_points - train_images[i], axis=1) # 将相距最近的中心点所属的类作为该样本的类 r[i][np.argwhere(distance==np.min(distance))[0][0]] = 1 return r

将每个样本成功归类后就要更新中心点的位置。这里的中心点位置需要到该类中各个样本点的距离最短，因此是各个样本点的平均位置。同样，这里采用不同的距离度量方式也可以产生不同的结果。

```python

更新中心点位置

def updateCenterPoints(r, train_images, k): center_points = np.empty((k,train_images.shape[1])) for i in range(k): # 类内样本特征值之和除以样本数，即平均特征值 center_points[i] = np.sum(train_images*(np.repeat(r[:,i].reshape(1,-1),\ train_images.shape[1],axis=0).T),axis=0) / np.sum(r[:,i]) return center_points ```

2.1.3 聚类标签的获取

现在我们得到了十个聚类的中心点。经过训练，我们期望这些点能够对数据进行分类。然而我们不知道每个中心点对应的是哪一个标签。因为训练集中，每个类中有多个样本，可以让这些样本进行投票，每个样本为自身表示的标签进行投票，票数最多的标签就作为该中心点所代表的类的标签：

python labels = (genLabels(r, train_labels, k)).astype(np.int16)

```python

对每个聚类打上标签

def genLabels(r, train_labels, k): labels = np.empty(10) # 第一层循环遍历每个聚类 for i in range(k): # 第二层循环统计该类中样本属于某一类的个数 max_count = 0 max_label = -1 # 分别对每个标签进行投票 for j in range(k): tmp = np.sum(train_labels[r[:,i]==1]==j) # 记录当前票数最多的标签与对应的票数 if tmp > max_count: max_count = tmp max_label = j labels[i] = max_label return labels ```

2.1.4 验证结果

在验证时，只需要比较验证样本与各个中心点的距离，选择距离最近的中心点所代表的类的标签作为预测结果，与实际的验证样本标签相比较即可。

python right = 0 for i in range(test_images.shape[0]): distance = np.linalg.norm(center_points - test_images[i], axis=1) predict = labels[np.argwhere(distance==np.min(distance))[0][0]] if predict == test_labels[i]: right+=1 print(right,right/test_images.shape[0])

2.2 GMM

在GMM方法中，我们将不同的训练样本看做一个高斯混合模型的分布。不同的标签对应不同的分布，而每个分布由多个高斯分布组合而成。因此，对于每一类的分布都需要单独训练。

2.2.1 数据预处理

在GMM算法中，需要计算每个样本属于某个分布中的高斯分布的概率。而当特征向量的维数很高时，高斯分布的概率密度函数在特定点的大小就会特别的小。本次的实验中每个样本的维度为784，这么高的维度是不能够应用GMM的，因此首先要考虑对数据进行降维。这里我采用了 sklearn.decomposition 中的PCA模型，使用主成成分分析的方法对数据进行降维：

python pca_model = PCA(n_components=50) pca_model.fit(train_images.T) train_images = pca_model.components_.T pca_model.fit(test_images.T) test_images = pca_model.components_.T

每个GMM应该用于拟合一类的样本，因此我们需要给样本进行分类。按照标签将训练样本分为十类，每一类单独用来训练一个GMM：

```python

将训练数据按照类别分组

type_num = 10 # 不同标签的个数 tmp = [[] for i in range(type_num)] for i in range(train_num): tmp[train_labels[i]].append(train_images[i])

train_images[i][j]表示类型为i的第j个样本

train_images = tmp[:][:]

```

2.2.2 训练过程

用每一类单独训练一个GMM：

```python

设置基本参数

k = 10 # 每个GMM中高斯模型的个数 t = 100 # 单个GMM迭代次数 GMM = [] # 记录每个类的GMM for i in range(type_num): GMM.append(genGMM(k,t,np.asarray(train_images[i]))) ```

训练单个GMM时，首先设置GMM的基本参数和初始值。需要混合高斯模型中，每个高斯分布的均值 gauss_means 、每个高斯分布的协方差矩阵 gauss_var ，以及这些高斯分布在模型中所占的比例 pi 。同时还需要样本属于某个分布的概率值 gamma 。分布的均值由数据集中随机抽取 k 个样本得到，协方差矩阵初始化为单位矩阵。比重和概率一开始都均等。

python def genGMM(k,t,train_images): # 每个高斯分布的均值，初始化为随机的k个样本点的位置 train_num = train_images.shape[0] gauss_means = np.asarray(train_images[random.sample([i for i in range(train_num)],k)]) # 每个高斯分布的协方差矩阵 gauss_var = np.asarray([(1*np.eye(train_images.shape[1])) for j in range(k)])# 对角且相等 # gamma[i][j] 表示样本i属于第j个高斯分布的概率 gamma = np.ones((train_num, k)) / k # 每个分布的比重 pi = gamma.sum(axis=0) / gamma.sum()

下面开始迭代更新参数。

python for i in range(t):

本次实验采用EM算法来训练GMM。EM算法的执行过程简单来说，就是在给定的参数下得到对数似然函数的期望，然后进一步更新参数，使得原来的参数下得到的对数似然函数取得最大值。

E步骤的过程如下：

```python

E-step

计算对数似然函数

pdf = np.zeros((train_num, k)) for j in range(k): pdf[:, j] = pi[j] * multivariate_normal(gauss_means[j], gauss_var[j],allow_singular=True).pdf(train_images) log_likehood = np.mean(np.log(pdf.sum(axis=1))) print(log_likehood) ```

这里，我使用了 scipy 库的 multivariate_normal 来生成单个多元高斯分布模型。给定该分布的均值和协方差矩阵，可以得到其概率密度分布。调用 pdf 功能，给出样本，就可以得到该样本在该高斯分布下出现的概率。用 pdf[i][j] 表示在该高斯混合模型下，第 i 个样本属于第 j 个高斯分布的概率。

然后，进行M步骤，按照先前算出来的公式更新参数，使得当前的概率密度期望达到最大值：

```python

M-step

更新各个分布的参数

gamma = pdf / pdf.sum(axis=1).reshape(-1,1) pi = gamma.sum(axis=0) / gamma.sum() for j in range(k): gauss_means[j] = np.average(train_images, axis=0, weights=gamma[:, j]) cov = [np.dot((train_images[t]-gauss_means[j]).reshape(-1,1),(train_images[t]-gauss_means[j]).reshape(1,-1)) for t in range(train_num)] cov_sum = np.zeros((train_images.shape[1], train_images.shape[1])) for l in range(train_num): cov_sum += gamma[l][j] * cov[j] gauss_var[j] = cov_sum / np.sum(gamma[:,j]) ```

每个高斯混合模型需要保留各个高斯分布的均值、协方差，以及他们的权重，这三个参数决定了一个完整的高斯混合模型：

python return [gauss_means, gauss_var, pi]

2.2.3 验证结果

在得到了所有的高斯混合模型后，需要测试时，将测试样本在每个高斯混合模型下算出其对数似然函数值，用于表示它符合各个高斯混合模型的概率。选择概率最高的那一个模型对应的标签作为预测结果：

python right = 0 for l in range(test_images.shape[0]): prob = [] # 依次使用每个GMM进行预测 for i in range(type_num): pdf = np.zeros(k) # 用每个模型中的每个高斯分布得到样本分布概率 for j in range(k): pdf[j] = GMM[i][2][j] * multivariate_normal(GMM[i][0][j], GMM[i][1][j],allow_singular=True).pdf(test_images[l]) # 计算对数似然 prob.append(pdf.sum()) prob = np.asarray(prob) # 选择对数似然最高的GMM对应的标签作为预测结果 ans = np.argwhere(prob==np.max(prob))[0][0] if ans == test_labels[l]: right+=1 print(right, right/test_images.shape[0])

三、实验结果与分析

3.1 K-means

使用MNIST数据集，同样进行100次迭代，K-means算法中，如果使用随机初始化中心点，准确率为58.9%；如果是基于距离选择的中心点，准确率为59.45%。二者差别不大。

K平均聚类的结果高度依赖于初始化的中心点。选择中心点的策略不同的话可能会得到不同的结果。我们希望选择的初始点有各个类别的代表性，能够很好地区分各个类别。这就要求选择的初始点相距较大。初始时如果是随机选择中心点，即随机选择数据样本作为初始中心，有可能选择了距离很近的多个样本作为初始中心从而导致结果不好。当然也有可能随机选择的中心点较优。总的来说，存在选择较差点的风险。为了避免选到太近的点作为中心点，可以使用基于距离的方法，即一开始随机选一个样本作为中心点，其他时候选择离各个中心最远的样本作为中心点。但是如果这样选择的话，问题在于可能选到异常值，导致聚类结果不准确。更好的方法是结合二者的思想，设定一个距离阈值，在所有超过距离阈值的点中随机选择，这样既避免了选择的点太近，又可以减少选到异常点的概率。

MNIST数据集为手写数字图片的集合。可以想见，相同的位置的像素点，不同的数字更有可能不同，而相同数字更有可能相同。K平均算法处理这样的数据是合理且有效的。

3.2 GMM

使用EM训练的GMM算法，初始化数据降维到50，每个GMM含有50个高斯分布，迭代10次，如果协方差矩阵初始化为对角且元素相等，准确率为37.86%；如果对角且不相等则为35.23%。下面的分析以协方差矩阵初始化为对角且元素相等的情况为例。

下图为第一个GMM训练时，对数似然函数值关于训练次数的变化：

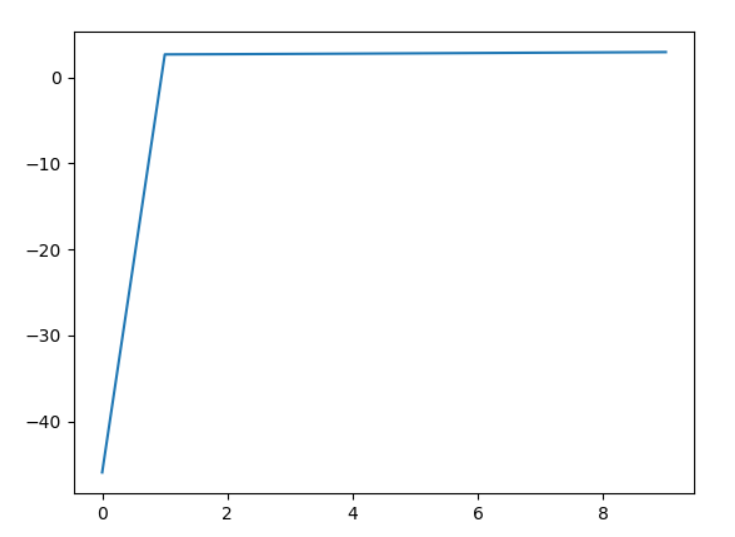
模型很快收敛了，但最终的对数似然函数的数值仍然较小，且几乎收敛，说明模型已经尽可能地拟合了数据，但拟合效果仍然不理想，模型不能很好地表示数据的分布。通过输出结果，我发现0、6等标签出现的概率高于其他标签，这说明这几个标签对应的GMM能更好地表示整个数据集，因此在这几个模型下会有更高的对数似然值，甚至比实际标签对应的模型算出来的对数似然值更高。这也侧面体现了模型拟合性能的不足。

可以看到，GMM算法的准确率非常低，而且实际训练过程中，训练时间相较K-means也更长。这应该是数据维度导致的。本次实验处理的数据维度高达784，而单个多变量高斯函数随着维度的上升，概率密度函数会越来越扁平。也就是说，在高维空间上，由高斯分布拟合的数据的概率会非常非常小，即便是在概率最大的均值处也会相当小。高达784维的数据根本不能简单地使用GMM算法运算。使用PCA方法降维又会产生样本信息的损失，且样本本身也不一定符合高斯分布，由此导致了结果性能较差。GMM更适合样本特征向量维度较小的情形。

总的来说，在MNIST数据集下，相比EM训练的GMM算法，K-means算法有着更好的性能。