1. 实验目的

实现一个 k-means 算法和混合高斯模型，并且用 EM 算法估计模型中的参数。

2. 实验要求

用高斯分布产生 k 个高斯分布的数据（不同均值和方差）（其中参数自己设定）。
用 k-means 聚类，测试效果；
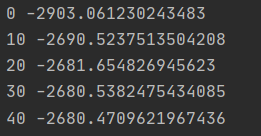
用混合高斯模型和你实现的 EM 算法估计参数，看看每次迭代后似然值变化情况，考察 EM 算法是否可以获得正确的结果（与你设定的结果比较）。
应用：可以 UCI 上找一个简单问题数据，用你实现的 GMM 进行聚类。

3. 设计思想

3.1 K-means 算法

k 均值聚类算法（k-means clustering algorithm）是一种迭代求解的聚类分析算法，其步骤是，预将数据分为 K 组，则随机选取 K 个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。

算法为：先随机选取 K 个对象作为初始的聚类中心。然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了，每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是以下任何一个：

没有（或最小数目）对象被重新分配给不同的聚类。
没有（或最小数目）聚类中心再发生变化。
误差平方和局部最小。

3.2 GMM 算法

GMM，高斯混合模型，也可以简写为 MOG。高斯模型就是用高斯概率密度函数（正态分布曲线）精确地量化事物，将一个事物分解为若干的基于高斯概率密度函数（正态分布曲线）形成的模型。

GMM 相对 K-means 是比较复杂的 EM 算法的应用实现。与 K-means 不同的是，GMM 算法在 E 步时没有使用“最近距离法”来给每个样本赋类别（hard assignment），而是增加了隐变量 γ。γ 是(N,K)的矩阵， γ[N,K]表示第 n 个样本是第 k 类的概率，因此，具有归一性。即的每一行的元素的和值为 1。

GMM 算法是用混合高斯模型来描述样本的分布，因为在多类情境中，单一高斯分布肯定是无法描绘数据分布。多个高斯分布的简单叠加也无法描绘数据分布的。只有混合高斯分布才能较好的描绘一组由多个高斯模型产生的样本。对于样本中的任一个数据点，任一高斯模型能够产生该点的概率，也就是任一高斯模型对该点的生成的贡献（contribution）是不同的，但可以肯定的是，这些贡献的和值是 1。

4. 实验过程

4.1 算法设计

高斯分布参数：

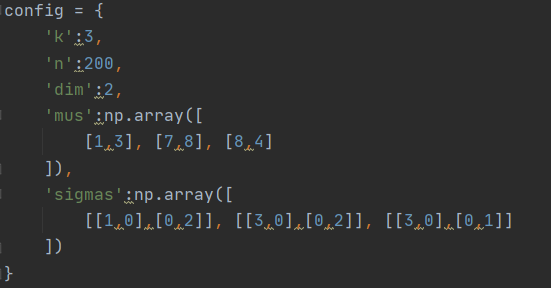
E 步：

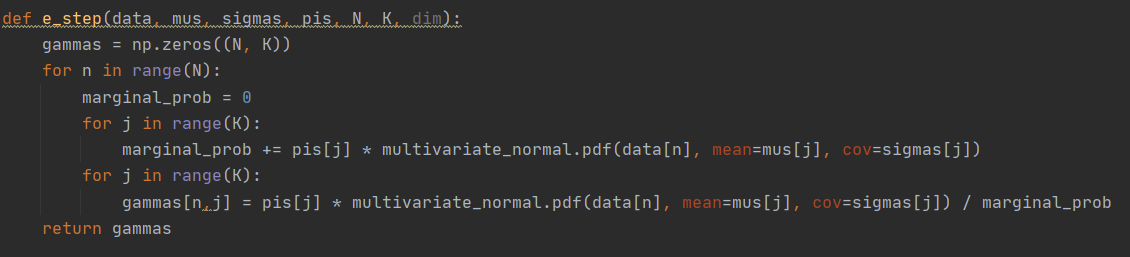
M 步：

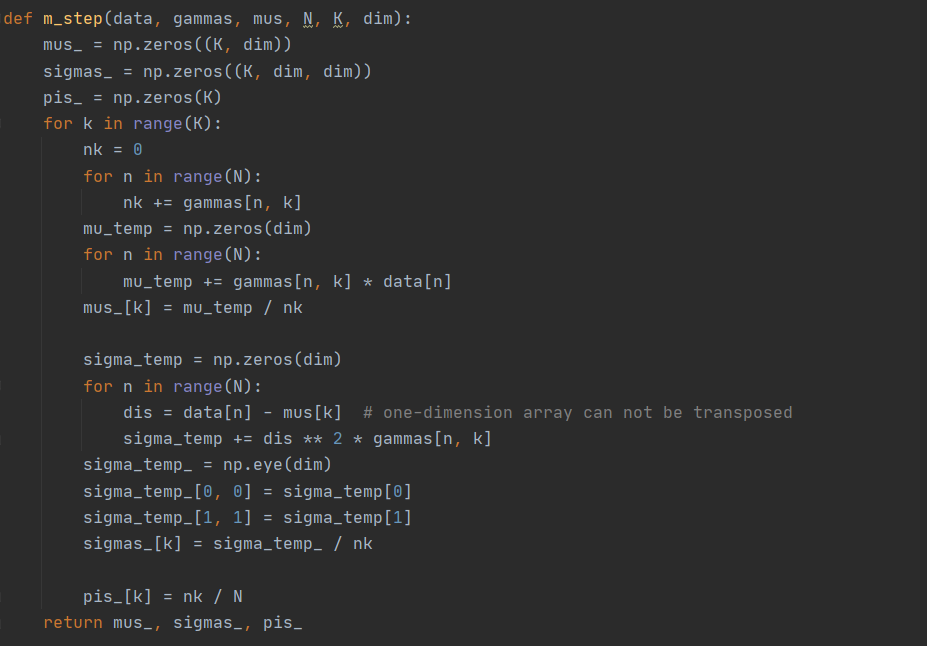
极大似然估计：

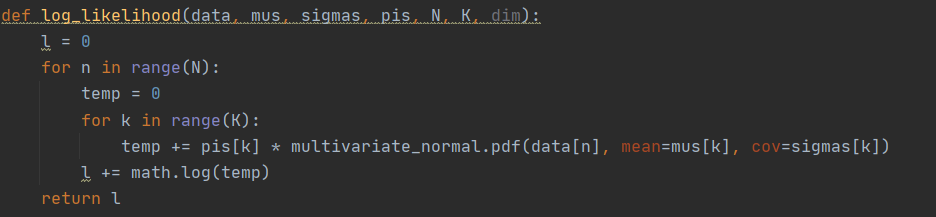
4.2 实验结果

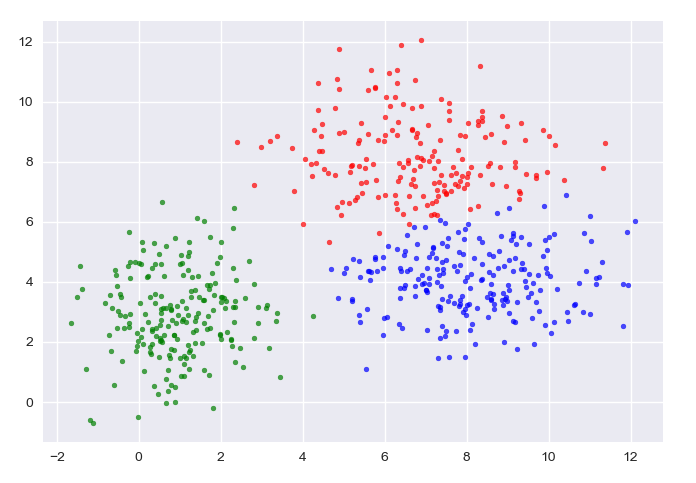
自生成数据，K-means：

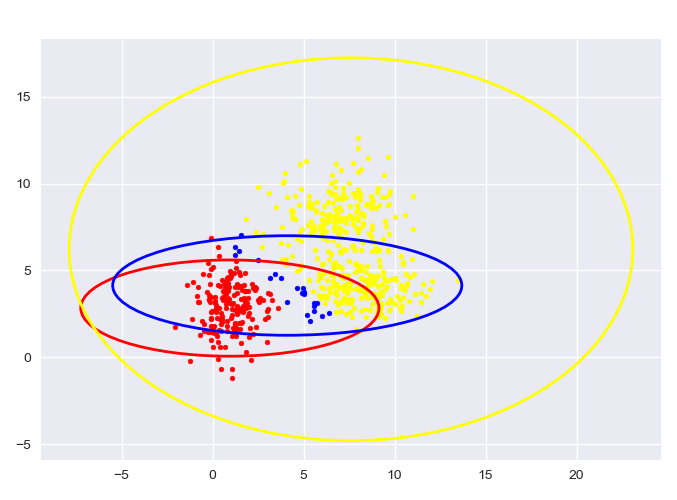
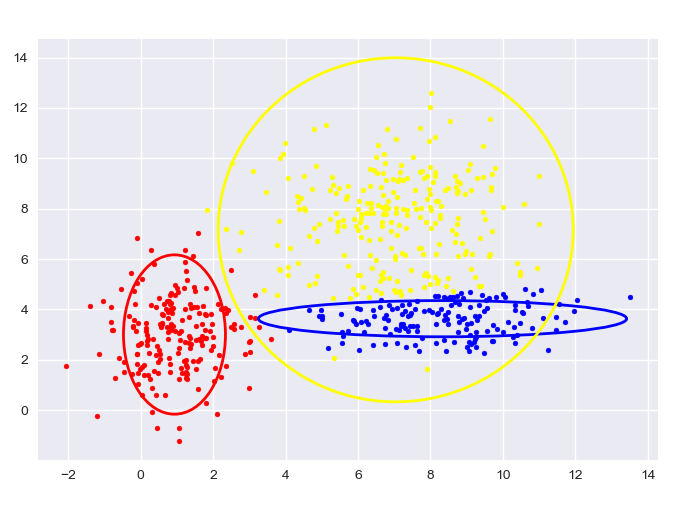
自生成数据，GMM：

图中给出了每一阶段的样本分类情况和置信椭圆。

最后带有填充的透明置信椭圆为生成数据的真实椭圆。

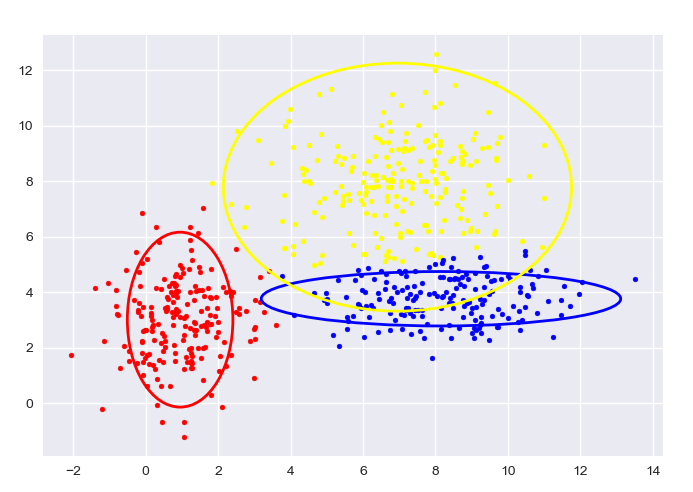
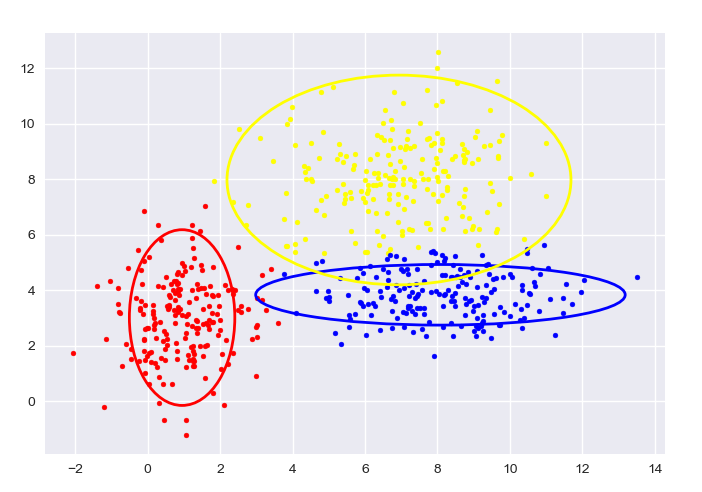
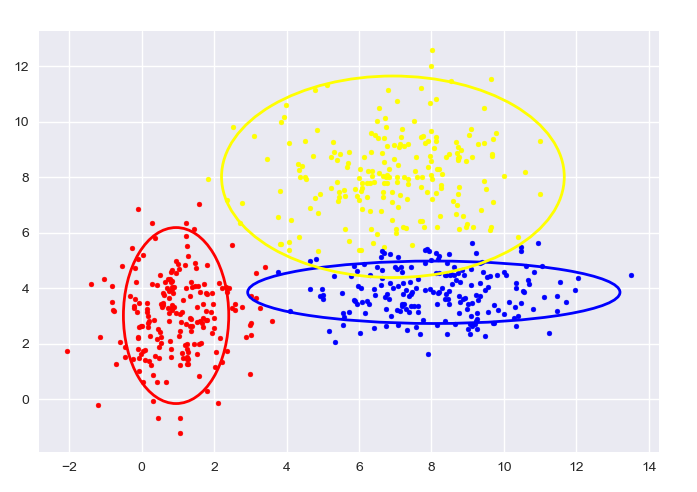
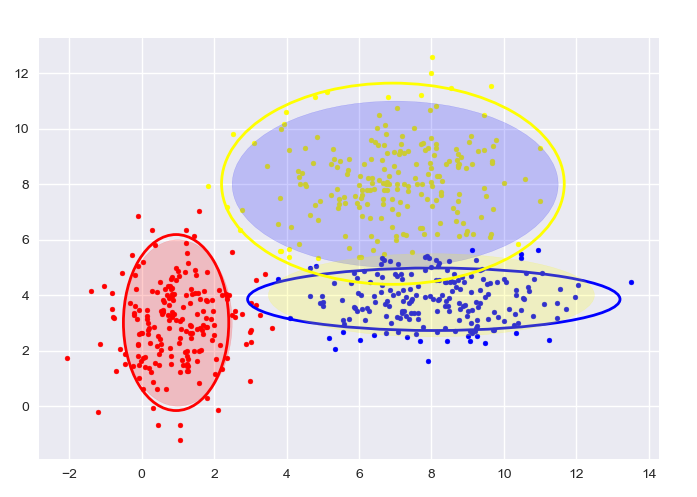
5. 实验结论

K-means 和 GMM 都是 EM 算法的体现。两者共同之处都有隐变量，遵循 EM 算法的 E 步和 M 步的迭代优化。不同之处在于 K-means 给出了很多很强的假设，比如假设了所有聚类模型对总的贡献是相等的（平均的），假设一个样本由某一个特定聚类模型产生的概率是 1，其他为 0. 而 GMM 用混合高斯模型来描述聚类结果。假设多个高斯模型对总模型的贡献是有权重的，且样本属于某一类也是由概率的。两者都能较好的解决简单的分类问题，但存在着可能只取到局部最优的问题。

初值的选取对 K-means 和 GMM 的效果影响较大。K-means 的初值选取通常是给定聚类个数 k 和随机选取初始聚类中心。而对于 GMM 来说，如果初始高斯模型的均值和方差选取不好的话，可能会出现极大似然值为 0 的情况，即该样本几乎不可能由我们初始的高斯模型生成。另外在实验过程中还会出现协方差矩阵不可逆的情况。