基于python的贪吃蛇游戏

1、项目简介

本项目为贪吃蛇游戏及自动寻路算法的实现。本项目分为两个小部分。

1.1 贪吃蛇游戏

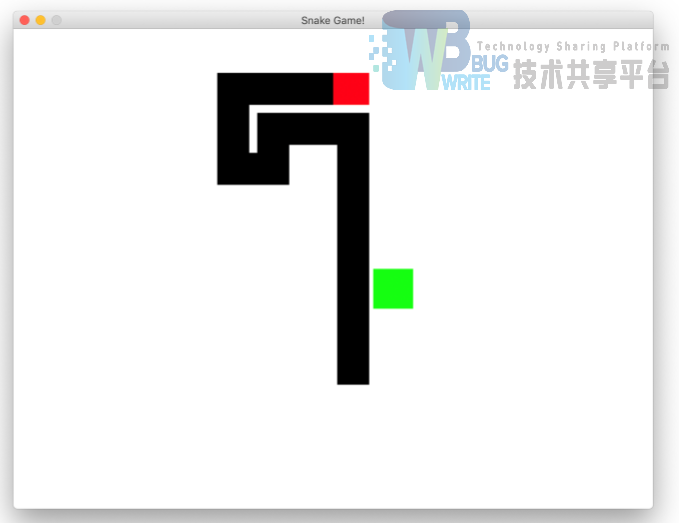
本项目实现了带有 UI 界面的贪吃蛇游戏。玩家可以通过键盘操控贪吃蛇（蛇身黑、蛇头红），追逐随机产生的水果（绿）。

在贪吃蛇游戏中，贪吃蛇会在一个二维平面（称为地图）上运动。每一轮，玩家控制贪吃蛇向前一个单位，向左一个单位或向右一个单位（不允许静止不动）。若贪吃蛇碰撞到地图的边界或自己的身体，则游戏失败。若贪吃蛇的蛇头触碰到水果，则蛇身延长一个单位。当蛇身能完全占满整个地图后，游戏胜利。

1.2 自动寻路算法

自动寻路算法为贪吃蛇赋予一定的智能，让其能正确地完成游戏。此处的 ‘‘正确’’ 有两层含义。

当贪吃蛇能触碰水果时，其应主动沿较优路接近水果
任何时候，当下一步行动可能造成贪吃蛇的死亡时，贪吃蛇应避免该行动目前实现自动寻路的方法有很多，例如：
朴素贪心算法
保守 Hamilton 回路算法
改良 Hamilton 回路算法
遗传算法
改良的贪心算法

这些方法会在节7作详细描述。其中本项目使用的是改良的贪心算法。

NOTE ：本项目使用的改良贪心算法，可以证明其正确性。它的效率和准确度都是所有算法中最高的。

2、项目闪光点

效果优良的寻路算法
无向图最长路近似算法
解耦的实现 TODO

3、环境与运行

3.1 运行环境介绍

运行本项目代码需 Python3.5 及以上和 Pygame 组件库。一种参考的安装和运行方法见代码 1。

在代码1中，需要预安装 python 虚拟环境管理工具 conda（并非必要），并使用 pip 安装 pygame 组件库。在安装完毕后，使用 cd 命令进入 code/目录，并直接运行 main.py 程序即可。

python $ conda create --name game python=3.7 2 $ pip install pygame $ cd code/ 4 $ python main.py

3.2 运行方法和使用方法

3.2.1 程序运行

使用小节3.1介绍的方式（或其他等价方式）安装环境并运行 main.py 代码。以下假设程序已正常运行。

3.2.2 配置文件

本游戏给予玩家很大的可配置性，许多参数都存放在配置文件 (conﬁg.json) 中。这里提供了一份默认的配置文件（代码 2）, 但用户可以随意按需修改。

NOTE ：在 main.py 文件的同一目录下，必须存在一份 conﬁg.json 文件，否则游戏因缺少参数而无法运行。

在配置文件中，window-width 和 window-height 分别指定游戏窗口的大小。block-size 指定游戏中一个 ‘‘块’’ 的大小（贪吃蛇每次以块为单位移动）。块必须能整除 window-width 和 window-height。speed 是游戏速度，决定贪吃蛇的移动间隔时间（秒）。auto 指是否开启 AI 自动寻路。

python { "window-width": 800, "window-height": 600, "block-size": 50, "speed": 0.3, "auto": true }

3.2.3 游戏键位

使用 W,S,A,D 分别控制贪吃蛇向上、下、左、右运动。使用 U 和 I 控制游戏的速度，U 加快游戏速度， I 减慢游戏速度。使用 Q 退出游戏。

(按下空格键以产生一份"output_ .log" 文件，用于 debug）。

4、代码文件介绍

4.1 主文件 main.py

main.py 调用了其他所有的文件，是玩家直接运行的程序。

该文件使用 Snake 类和 Fruit 类存储了地图信息，使用 Pygame 绘制了游戏窗口，使用 SnakeDrawer 和 FruitDrawer 为不断变化的 snake 和 fruit 更新绘制图像。同时，Pygame 还负责监听键盘事件，响应玩家的操控。main.py 还负责使用延时来处理游戏速度。

4.2 游戏类 snake.py 和 fruit.py

Snake 类和 Fruit 类分别定义在 snake.py 和 fruit.py 上。

Snake 类存储了贪吃蛇的内部状态，例如所有蛇身所在的坐标（特别地，蛇头看做第一段蛇身），蛇的当前方位等。Snake 类暴露了若干接口，用于设置蛇的当前走向、控制蛇向前一步，检验蛇是否处于非法状态等。

Fruit 类存储了水果的内部状态，例如水果的当前坐标。Fruit 类还实现了 generate 函数，产生下一个水果的出现位置。由于水果不能出现在蛇身占用的格子上，故 Fruit 的 generate 函数可能会被反复调用，直到得到的结果符合游戏要求。

4.3 寻路类 pather.py 和 solver.py

pather.py 是寻路类的主要模块，其中的类 PathSolve 是辅助工具，用于求出蛇头距离水果的最短路，以及蛇头距离水果和蛇尾的最长路。

NOTE : 无向图中的两点最长路是 NP-Hard 问题，但本项目使用了近似算法，在小规模数据中取得了等价于精确解的效果。

PathSolve 使用了广度优先搜索算法得到最短路。可以容易地将其拓展为 A-Star 算法获得更好的性能。但广搜的性能在此处已经足够好。同时，其采用了‘‘最短路拓展”的方法找到近似最长路，具体地说，它在最短路的基础上反复尝试将路拓展延长 2 个单位，直到无法进行任何的拓展为止。更详细的介绍见节 6。

solver.py 定义了 GredySolver 类。如名字所见，该类采用改良的贪心算法进行寻路。当蛇可以轻易吃到水果时，蛇会优先以最短路走向水果，否则，蛇会以最长路走向蛇尾。更详细的介绍见节 6。

5、贪吃蛇游戏的具体实现

5.1 常亮定义

在贪吃蛇项目中，定义以下的若干常量可以简化代码的书写，使得代码的可读性更好。

5.2 Snake 类的具体实现

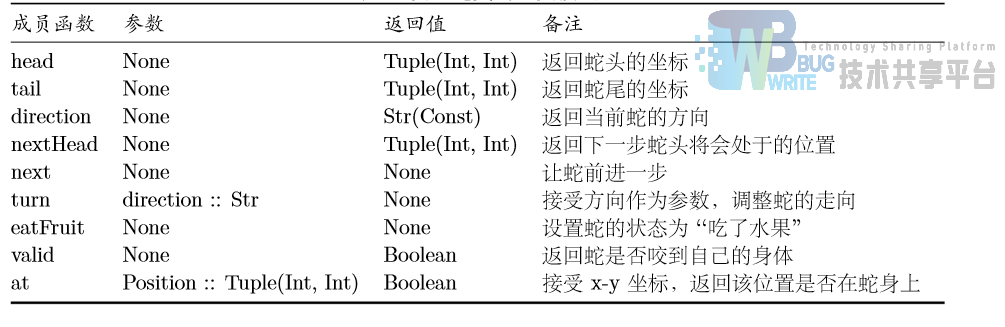
Snake 类定义了一系列接口。它们大致可以分为返回状态的接口和更新状态的接口。

返回状态的接口包括 head, tail, direction, nextHead, valid, at 等。

nextHead是必要的，这是因为如果蛇下一步前进时会触碰到水果，新的水果必须在同一时刻出现在地图上。知道蛇头下一刻处于的位置是有好处的。

at 用于判断地图上的某个方块是否被蛇身占用。在生成水果时会用到。水果必须生成在不被蛇身占用的方块上。

有副作用的函数包括 next, eatFruit 等。其中调用 next 后会使得蛇前进一个块。Snake 类中存储了蛇身的坐标以及蛇头方向。在调用 next 后，蛇头向前延伸一个单位，并把延伸的块的坐标插入到蛇身的第一个元素（.insert(0, *))。还要把蛇身的最后一个元素删除 (.pop())。

eatFruit 被调用后，蛇的内部状态会记录着当前吃到了一个水果 (hasEat = True); 在下一次 next 被调用时，不再把蛇身的最后一个元素删除（相当于蛇身变长一个单位）。无论怎样，在调用 next 后都会把吃到水果的状态置空 (hasEat = False)。

注意到许多函数是幂等的。幂等的意思是，这些函数连续调用一次以上的效果和只调用一次的结果是一样的。例如连续多次 turn(RIGHT)，或者多次调用 getHead。幂等的性质可以给编程带来极大的便捷。（此处留意，turn(RIGHT) 的 RIGHT 指的是绝对的右方，而不是指相对于蛇头的右方）。

5.3 Fruit 类的具体实现

由于 fruit 类的实现比较简单，故直接放上代码（代码 3）。

__init__ 函数主要读取了 conﬁg 的信息，设置了 width 和 height 两个内部状态。

函数 generate、where 和内部状态 last_generate 的设计是比较好的，我后续的许多代码都得益于这个接口而得到改进。

首先 generate 函数显式地产生随机坐标，将随机坐标记录到 last_generate 上，并返回。fruit 类会一直维护着最后一次产生的随机坐标。事实上，这个 ‘‘最近一次的随机坐标对’’ 恰好就是游戏当前水果所在的地点。

where 函数返回

如果 last_generate 为空，则调用 generate 后，再返回 last_generate
否则，直接返回 last_generate 这个设计使得用户可以安全地随时调用 where 函数，且确保 where 函数有合法的返回值。只有在当前的状态过期时（水果被吃掉了），才有必要调用 generate 函数重新生成水果

NOTE : 最近一次产生的随机坐标，是当前游戏中水果的位置坐标。

python class Fruit: def __init__(self, config): self.config = config # some code to get width from ‘config‘ self.width = ... # some code to get height from ‘confgi‘ self.height = ... self.last_generate = None def generate(self): x = random.randint(0, self.width - 1) y = random.randint(0, self.height - 1) self.last_generate = (x, y) return (x, y) 14 def where(self): if self.last_generate is None: self.generate() return self.last_generate

5.4 Drawer 和相关类的具体实现

Drawer 相关的类有三个。分别是 Drawer, SnakeDrawer 和 FruitDrawer。其中 Drawer 类是后两个类的基类。

5.4.1 Drawer 基类的实现

Drawer 类定义了两个基本函数 (代码 4)，分别是_basic_draw 和 _toLeftTop。下划线代表这两个成员函数是保护 (protected) 成员函数。

这里的实现牵扯到一些 pygame 的使用细节，但大体的思路是很明确的。本项目中，水果、蛇身和蛇头都采用方块来表示。成员函数 _basic_draw 封装了画方块这一操作。

self.rect 缓存了一个边长为 blk 的方块信息，其中 blk 是从配置文件中读取的内容。在实际画出方块时，需要对 self.rect 作（以窗口左上角为原点的）平移操作。平移时只需要修改 self.rect 对象中的 topleft 属性即可。该属性是个 getter/setter 语法糖，在该属性被修改时，会触发 self.rect 修改其他相关属性（例如 left, top 等），以维持方块的一致性。

_basic_draw 函数首先对方块作平移，随后在 Surface 上画出这一方块。在函数 _basic_draw 中，Surpface 是对象 screen。screen 是代表整个窗口的 Surface，由 Drawer 类被构造时传入。

_toLeftTop 接受坐标 x 和 y，返回 x 行 y 列的方块的 topleft 值。

5.4.2 SnakeDrawer SnakeDrawer 的成员函数

其中 __remove 和 __draw 函数调用了基类的函数 _basic_draw。函数 next 是有副作用的函数，它和 Snake 类的耦合度比较高。它的作用是，调用 Snake 函数的 next 方法，让蛇向前行走一步，并仅仅更新蛇头和蛇尾两个方块。这样的目的是加快程序的运行效率。绘制图形和刷新窗口是非常费时的操作，加快程序运行方法有两个层面。

尽可能减少窗口的刷新范围
尽可能较小窗口的刷新频率 SnakeDrawer 和 Snake 类在 next 方法上强耦合，但能 ‘‘减少窗口刷新范围’’

SnakeDrawer 类还有一个 draw 成员函数，它的作用是画出全部的蛇身。在整个游戏窗口初始化时，这个函数会被调用。但随后，对 snake 的所有绘图都仅适用 next 函数。

python class Drawer(): def __init__(self, screen, config): self.blk = int(config[’block-size’]) self.rect = pygame.Rect(0, 0, self.blk, self.blk) self.screen = screen def _basic_draw(self, x, y, color): self.rect.topleft = self._toLeftTop(x, y) pygame.draw.rect(self.screen, color, self.rect) def _toLeftTop(self, x, y): return (x * self.blk, y * self.blk)

5.5 FruitDrawer FruitDrawer 的定义

该实现比较简单，故直接附上源码。它仅提供了 draw 接口，它调用了 Fruit 的 where 成员函数，画出水果的当前位置。

6、自动寻路算法的具体实现

本节介绍自动寻路算法的具体实现。它基于几个简单的搜索算法，在整体上使用贪心的思想。

6.1 寻路算法介绍

常用的寻路算法有许多种，以下详细见介绍。

python class FruitDrawer(Drawer): def __init__(self, screen, config, fruit): Drawer.__init__(self, screen, config) self.fruit = fruit self.width = int(int(config[’window-width’]) / config[’block-size’]) self.height = int(int(config[’window-height’]) / config[’block-size’]) def draw(self): x, y = self.fruit.where() self._basic_draw(x, y, GREEN)

6.1.1 朴素贪心算法

朴素贪心算法采用最朴素的贪心法。在每一步中，直接搜索从蛇头到水果的最短路，并按该条路线前往水果。

该方法的优点是易于实现，思路简洁。但它的缺点也很明显。在贪吃蛇游戏中，局部最优解一般都不为全局最优解（且往往相差很远）。这不满足我们在??中提出的 ‘‘任意时刻贪吃蛇应避免死亡’’ 的要求。

如果贪吃蛇按箭头方向根据最短路吃到了水果，它会因所有的出口都被堵住而游戏失败。

很快可以看到，在朴素贪心算法的基础上添加 ‘‘无向图最长路近似算法’’，结合起来得到的改良版本可以获得很好的性能。

6.1.2 保守的 Hamilton 回路算法

朴素 Hamilton 回路算法的思路很简单。其尝试在地图上构造一条哈密顿回路，然后永远按照该回路在地图上无限循环地走。显然这个算法是绝对正确的，而且贪吃蛇绝对不会死亡。但这却不满足提出的‘‘沿较优路前往水果’’这个目标。

除此之外，这个算法还有一个隐含的要求，就是地图需要包含一条哈密顿回路。事实上这点是无法确保的。对于不存在哈密顿回路的图，这个算法可能会失效。

6.1.3 随机神经网络算法

随机神经网络的方法是，使用纯随机（而非梯度下降）的方式优化参数。评价神经网络的标准也不再是交叉熵或准确度，而是 ‘‘贪吃蛇每局游戏的平均长度’’。

具体来说，首先随机创建 n 个神经网络。每个神经网络的参数均来自独立的随机分布。神经网络的输入是各种提前选定的属性，例如 ‘‘蛇头距离水果的距离’’，‘‘蛇头左侧是否有障碍’’ 等等。神经网络的输出是超参数，在整个模型训练中不变。神经网络的输出维度是 3，分别表示 ‘‘直行’’、‘‘左转’’ 和 ‘‘右转’’ 的自信度。

使用这 n 个随机创建的神经网络玩贪吃蛇游戏，记录他们的平均蛇长。取出效果最好的 m 个神经网络（m 一般比较小）。这为一轮训练。在这 m 个神经网络的基础上，加入随机的偏差，再次产生 n 个随机的神经网络。如此重复，直到最后的神经网络能取得比较好的效果。

但这个算法有很大的缺点。例如：

需要人工选定输入的特征。难以选择合适的输入特征
效果较差。目前大部分基于神经网络的算法都难以在贪吃蛇游戏中取得比较好的效果

6.1.4 改良的贪心算法

改良的贪心算法是本项目选择实现的算法，可以证明它不会使得贪吃蛇游戏失败，且在大部分情况下沿最短路前往水果。它的主要思路如下。

首先搜索一条蛇头到水果的最短路。然后假设贪吃蛇按照该最短路到达了水果。在此基础上，检查蛇头是否有路径到达‘‘蛇尾’’。如果能到达蛇尾，说明蛇一定存在一个策略保证存活（称此状态为安全状态）。如果不能，则说明蛇在吃了水果后的处境可能会 ‘‘危险’’，于是拒绝这个决策，选择在周围游荡，以‘‘拖延时间’’。

6.2 改良贪心算法的具体实现

6.2.1 流程和正确性证明

改良贪心算法的具体流程如下。为了寻找蛇 S1 的最佳方向 D

(a) 构造从蛇 S1 到水果的最短路 P1。如果 P1 存在，则执行 (b)。否则执行 (d)
(b) 构造一条虚拟的蛇 S2 ← S1，让 S2 前进并吃到水果
(c) 构造蛇 P2 从蛇头到蛇尾的最长路 P2。如果 P2 存在，那么 D 就是 P1 的第一个方向。否则，执行 (d)
(d) 计算蛇 S1 从蛇头到蛇尾的最长路 P3。如果 P3 存在，那么 D 就是 P3 的第一个方向。否则，执行 (e)
(e)（worst case）D 为远离水果的那个方向

对这个流程的相关解释如下：

在计算从蛇头到水果的最短路后，还要判断蛇 S2 到其蛇尾是否具有最长路。这里要注意

NOTE : 无向图的最长路算法是 NP-Hard 问题，此处使用了近似算法。在算法分析时，最坏情况可能退化到最短路。

若蛇 S2 到蛇尾有最长路，可以得出蛇 S2 到蛇尾必有路（显然）。可知，这样的走法是安全的，这是因为。

LEMMA : 当存在一条蛇头到蛇尾的路径时，贪吃蛇必不死。

该引理是整个算法乃至整个项目最重要的一个理论基础。其奠定了改良贪心算法的准确性。

要论证这个引理很简单。首先，蛇头是不可能 ‘‘追上’’ 蛇尾的，这是因为每当蛇头往前前进一步，蛇尾也会向前收缩一步。贪吃蛇只需要保证一刻不停地追逐蛇尾，就能保证必定不死。

于是贪吃蛇存在一种策略：

贪吃蛇按照从蛇头到蛇尾的路前进该策略可以保证贪吃蛇必定不死
这就证明了上述引理的正确性。这同时解释了步骤 (c) 的用意：保证蛇不死

在不那么好的场景下，有可能出现以下的局面：

蛇 S1 不存在蛇头到水果的最短路 P1（步骤 a 的错误分支）
蛇 S1 不存在从蛇头到蛇尾的最长路 P3（步骤 d 的错误分支）

当 P1 不存在，说明了目前无法短时间内到达水果的位置。那蛇就应该尽可能地 ‘‘绕远路’’，争取拖延更多的时间。同时绕远路也应该绕得安全，那么这个远路就应该是从蛇头到蛇尾的远路。这就是 (a) 的错误分支跳转到 (d) 的解释。

若 S1 不存在从蛇头到蛇尾的最长路，说明蛇在最坏情况下很可能已经进入了困境。算法中步骤 (e) 的方法是向原理水果的方向运动。这是最坏情况下的无奈之举。

NOTE : 从蛇头到蛇尾的最长路必定存在。这是因为 (a) 在游戏开始时，存在从蛇头到蛇尾的最长路，且 (b) 在游戏的每次 ‘‘状态转移’’ 时都保证蛇头到蛇尾的最长路存在。故实际上上一情况是不可能出现的。

6.3 最长路算法

6.3.1 算法思路

最长路算法的基本步骤如下

找到一条最短路
尝试拓展最短路，直到无法拓展为止具体地说，在最短路 p 上定位相邻的两个结点

对于这每组相邻的结点，尝试将他们从两个结点拓展到四个结点。例如相邻的结点 A 和 B 中，A 向左走一步可以到达 B（[Left]）。拓展时，尝试拓展 A 到 B 的路 [Down, Left, Up]。对称地，也可拓展为 [Up, Left, Down]。

尝试画一下图显然得到，每次拓展都是把相邻的 2 个结点拓展成 4 个结点（类似于田字）。

这个拓展算法显然不是精确解，但在绝大部分情况下却能取得几乎最优的效果。

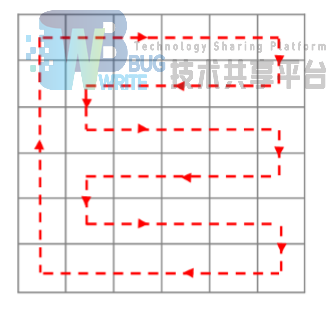
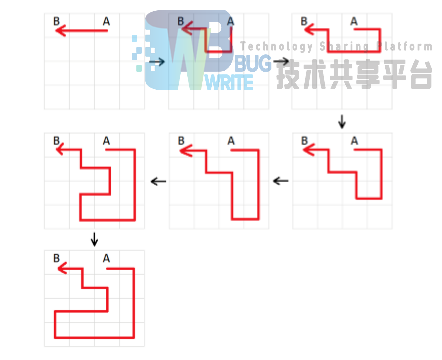
一系列图片是贪吃蛇沿着蛇头到蛇尾的最长路行进的示意图。图左一是贪吃蛇的初始状态。红方块是蛇头，贪吃蛇（蜷缩）在一团。

贪吃蛇很聪明地旋转着绕远路，同时留下一条空隙，给予自己回过头来回到蛇尾的机会。

贪吃蛇绕远路达到了右边界，准备返回。

贪吃蛇沿着左图一留下的 ‘‘空隙’’ 返回。逐步接近蛇尾。右图一中，贪吃蛇最终到达了蛇尾。

这个最长路几乎是最优解，因为它的路径覆了整个地图，除了右上方的一个方块。

6.4 算法实现

最长路近似算法的算法实现如所示。代码仅展示重要部分。

设变量 sp 存储的是最短路的走法中每一步的方向。算法一开始初始化 idx 为 0，cur 为最短路的第 idx 步的坐标。该算法反复尝试拓展第 idx 步，以求将第 idx 步拓展为 i0,i1,i2 三步。其中 i1 步就是第 idx 步， i0 和 i2 是额外拓展的两步，这两步走的是相反的方向（例如上和下，左和右）。如此一来， [i0,i1,i2] 三步的效果完全和 [idx] 步的效果一致。

举个例子，例如最短路中第 idx 步是向上走的。拓展算法会尝试把 [UP] 拓展为 [LEFT, UP, RIGHT] （分别对应 i0,i1,i2）。可以看到，i1 等于第 idx 步的走向。 i0 和 i1 是两个相反的方向，且与第 idx 步垂直。

以上的描述解释了代码6注释 (1) 处代码的作用。它使用 insert 方法，分别做 insert(idx,*) 和 insert(idx + 2, *)，以完成以上描述中的拓展。

NOTE : 在拓展之后，最短路的第 idx 步的方向发生了变化。但第 idx 步时所在的坐标不变。

NOTE : 算法会在最短路的 0∼idx 段完全拓展完毕后，再自增 idx，尝试拓展 idx+1 段。

python def longest_path(self, target): ’’’ @variable sp最长路列表 ’’’ # idx如正文描述 idx = 0 # 最短路的第idx步时的蛇头位置 cur = self.snake.head() while True: extended = False direction = sp[idx] # 最短路的第idx步的走向 if direction in [’U’, ’D’]: test_extend = [’L’, ’R’] # 可能的拓展方向 else: assert(direction in [’L’, ’R’]) test_extend = [’U’, ’D’] # next_cur是cur沿着最短路走一步得到的结点 next_cur = self.pos_move(cur[0], cur[1], direction) for d in test_extend: # d是可能的拓展方向 # t1和t2分别是cur和next_cur朝着方向d移动一步得到的结点 t1 = self.pos_move(cur[0], cur[1], d) t2 = self.pos_move(next_cur[0], next_cur[1], d) # 如果t1和t2结点是能拓展的（该块在地图区域内且该块没有被占用） if self.__exstendable(*t1, game_map) and self.__exstendable(*t2, game_map): extended = True # (1) sp.insert(idx, d) sp.insert(idx + 2, self.rev_map[d]) # 将t1和t2的所在块设置为占用 x, y = t1 game_map[y][x] = ’X’ x, y = t2 game_map[y][x] = ’X’ break # 最短路从0到idx这一段已经完全无法拓展了。将idx加1 if not extended: cur = next_cur idx += 1 40 if idx >= len(sp): break return True, sp