基于python实现通过真值表判断一个逻辑表达式

一、设计要求

1．问题描述

一个逻辑表达式如果对于其变元的任一种取值都为真，则称为重言式；反之，如果对于其变元的任一种取值都为假，则称为矛盾式；然而，更多的情况下，既非重言式，也非矛盾式。试写一程序，通过真值表判断一个逻辑表达式属于哪一类。

2．需求分析

逻辑表达式从终端输入，长度不超过一行。逻辑运算符包括“|”，“&”和“~”,分别表示或、与和非，运算优先程度递增，但可以由括号改变，即括号内的运算优先。逻辑变元为大写字母，表达式中任何地方都可以含有多个空格符。
若是重言式或矛盾式，显示“True forever”或“False forever”，否则显示“Satisfactible”。若用户对表达式中变元取一组值，程序就求出并显示逻辑表达式的值。在判断的结果下方同时列出真值表。
对于一个简单的表达式求值运算规则如下：

a) 从左至右依次计算。

b) 先取反，然后相与，后相或。

c) 先括号内，后括号外。

二、准备知识

我们可以将逻辑表达式的计算类比算术表达式的计算，通常借助堆栈来实现按运算符的优先级完成表达式的求值计算：一个是存放运算符的栈，另一个是存放变量或中间结果的栈。回顾一下中缀表达式转后缀表达式并计算的计算过程：

1、任何中缀表达式都由运算数，运算符，括号这三部分组成，其中括号的优先级最高，其次是乘除，最后是加减。

2、从左到右遍历中缀表达式，若遇到运算数时，则直接将压入数据栈。

3、若为运算符，以下几种情况直接将符号入栈：

栈为空；栈顶为左括号；该符号优先级比栈顶符号的优先级高。

4、若遇到右括号，表达括号内的中缀表达式已经扫描完毕，则执行计算步骤：从运算符栈弹出一个运算符号，从数据栈弹出两个数字进行一次运算并将结果入栈。重复此步骤直至遇到左括号，将左括号出栈。

5、如果该运算符的优先级小于或等于栈顶运算符的优先级时，重复4中的计算步骤，直到运算符栈空或栈顶为左括号。

6、最后扫描到中缀表达式的末尾，继续执行之前的计算步骤直到运算符栈空。

三、概要设计

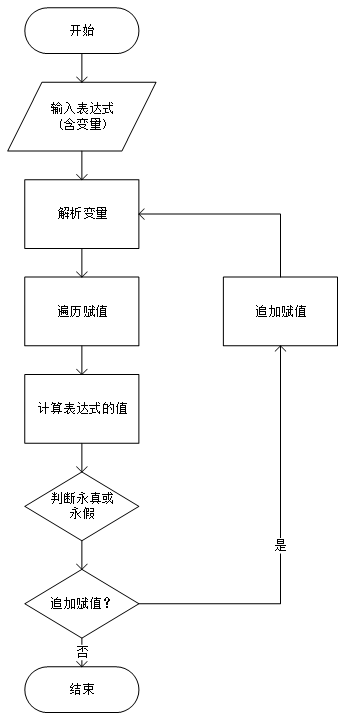
算法整体流程

如图figure1所示，我们算法的整体思路非常清晰；对于给定的逻辑表达式，我们先解析得到所有的变元，然后我们依次给变元赋值0和1；对于由n个变元组成的逻辑表达式，那么最终将得到2^n个不含任何变元的逻辑表达式；最后我们通过将这2^n个表达式一一计算得到真值表；通过真值表判定该逻辑表达式是否是重言式或者矛盾式；对于有追加的赋值，一种方法是直接查刚才计算得出的真值表，另一种途径是提前将追加的变元赋值，然后再解析、算真值表；为了代码的复用，我们使用了第二种方法。

四、详细设计

代码的整体结构如下所示，我们采用了面向对象的编程思想；定义LogicExpression类完成所有功能; 定义字典代表所有字符符号的优先级；定义__init__方法完成对象的初始化；定义parse方法完成变元的解析；定义generate方法完成真值表（变元部分）的生成；operate方法、process方法、solve方法均为具体计算表达式的方法；定义main方法整合所有计算过程；定义conclusion方法完成最后表达式的判定；

python classLogicExpression: priority = { '(': 4, '~': 3, '&': 2, '|': 1 }# 定义符号的优先级 def __init__(self, expression) def parse(self): def generate(self): def operate(self, symbol, arg): #不定长参数 def process(self, data, opt): def solve(self, exp): def main(self): @property def conclusion(self):

1.输入表达式

初始化部分非常简单,只是获取用户输入的表达式并删去多余的空格

python def __init__(self,expression): self.expression = expression.replace(' ','') #初始表达式、并删掉多余空格

2.解析变量

而解析表达式，获得变元这部分我们使用了python的正则表达式模块，我们规定变元的命名标准同代码中变元的命名标准相同；此外用set去除出现过不止一次的变元；最后按照变元的原始顺序排序。

```python def parse(self): pattern = re.compile(r '[a-zA-Z_]w')# 变量规则与代码中变量定义规则相同字母、数字、下划线组合, 数字不能开头 vars1 = pattern.findall(self.expression)# 解析成变量列表(待去重) vars2 = list(set(vars1))# 去重 vars2.sort(key = vars1.index)# 保持原来顺序不变

return vars2 ```

3.遍历赋值

在编历赋值这块，我们使用了python的自建模块itertools.product函数快速生成组合元祖；然后直接将变元用0和1替换；在返回时，使用yield函数依次返回一种组合，减少内存开销；

```python def generate(self): l = [0, 1]

for case inproduct([l] len(self.vars)): #case为生成的组合元祖：两个变量的情况下为(0, 0)(0, 1)(1, 0)(1, 1) exp = self.expression

  for i in range(len(self.vars)):
      exp = exp.replace(self.vars[i], str(
          case [i]))

  yield exp# 使用python的迭代器依次返回代入值后的表达式

```

4.计算表达式的值

计算表达式的值(不带变元)是整个代码的核心；我们的思想是维护两个栈分别存放逻辑符号和逻辑值。遍历表达式中的所有字符，按照优先级规则和栈内情况具体决定压栈和出栈，具体标准请参照下图：

对于逻辑值直接进逻辑栈；
遇到 ) 则进行出栈计算直到逻辑符号栈顶为 ( ,并将 ( 出栈
逻辑符号直接进栈的三种情况：符号栈为空、符号栈顶为（、符号栈顶符号的优先级小于该符号，在这三种情况下直接进栈
其余情况下，根据栈顶符号类型，取出相应数量的逻辑值进行运算，然后压入逻辑值栈；如此往复，直至当前符号满足进栈规则3
最后如果符号栈尚有元素，则继续运算
逻辑值栈最后存在的值即为表达式的解

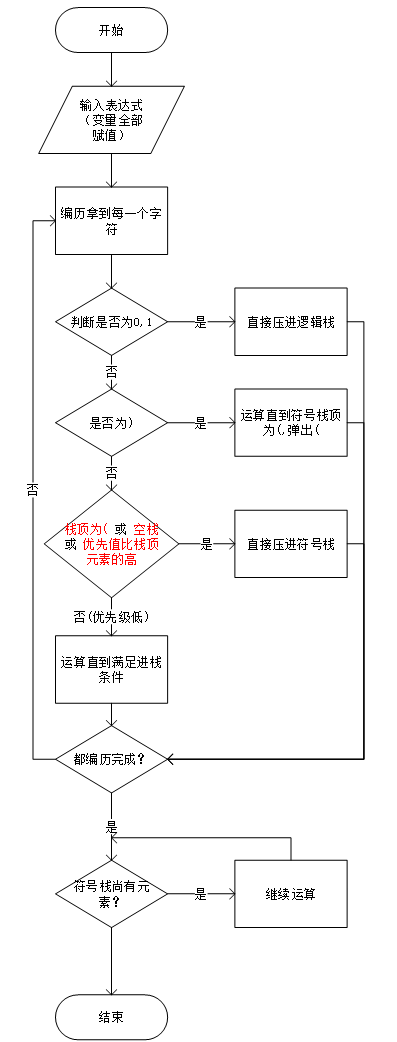
Figure2 出入栈标准

对应代码如下：

```python def solve(self, exp): data = []# 逻辑栈 opt = []# 操作符号栈

for i in exp: if i.isdigit(): #如果是数字则直接进逻辑栈 data.append(int(i) == 1) elif i == ')': #如果是) 则依次则开始从data栈和opt计算直到遇到(为止

      while opt[-1] != '(':
      self.process(data, opt)
       opt.pop()# 出栈(
          elifnot opt or opt[-1] == '('
          or self.priority[i] > self.priority[opt[-1]]: #
          符号进栈的三种情况: 符号栈为空、 符号栈头为(, ps: (进栈后优先值降为最低、 拿到的比栈中的优先级大
                   opt.append(i)

                  else :#优先级低需要先计算达到进栈条件后方能进栈
                   while opt and opt[-1] != '('
                  and self.priority[i] < self.priority[opt[-1]]:
                  self.process(data, opt)
                   opt.append(i)
                   while opt:
                  self.process(data, opt)
                   return data.pop()

```

其中还定义了两个子函数process和operate; processs 函数的作用是模拟取出符号栈和逻辑值栈元素运算的过程；operate函数作用是具体计算一个！&和|的运算，代码示例如下：

```python def operate(self, symbol, arg): #不定长参数 '' '

symbol: 逻辑符号~ & | arg: 逻辑值(不定长)

'' '

if symbol == '~' and len(arg) == 1: #~的情况 returnnot arg[0] elif symbol == '&' and len(arg) == 2: # & 的情况

return arg[0] and arg[1] elif symbol == '|' and len(arg) == 2: # | 的情况

return arg[0] or arg[1]

else : raise "operate error" def process(self, data, opt): '' '

data: 逻辑值栈存放true和false opt: 符号栈存放~ & | '' '

symbol = opt.pop()

if symbol == '~': logic1 = data.pop() data.append(self.operate(symbol, logic1))

return elif symbol in ('&', '|'): logic1 = data.pop() logic2 = data.pop() data.append(self.operate(symbol, logic1, logic2))

return ```

5.判断永真或者永假

最后判断是否永真或者永假，非常简单只要判断结果列表里面是否存在true（false）的情况

```python @ property def conclusion(self): ifFalsenotin self.results: return 'True forever'

elifTruenotin self.results: return 'False forever'

else : return 'Satisfactible' ```

6.网页部分

我们还设计了一个小网页用作交互，如下图所示：

网页部分使用python的flask引擎搭建；后端也很简单；分别对url的get请求和post请求做响应；post请求中调用实现好的LogicExpression类运算,而get请求则直接返回原始网页。

```python @ app.route("/", methods = ["GET", "POST"]) def main(): if request.method == 'POST': expression = request.form.get('expression') addition = request.form.get('addition')

if addition: expression = withAddition(expression, addition) le = LogicExpression(expression) varss, results, conclusion = le.vars, le.results, le.conclusion logic_table = tuple(product([ [0, 1] ] len(varss)))

return render_template("index.html", form = request.form, logic_table = logic_table, varss = varss, results = results, conclusion = conclusion) else : return render_template("index.html", form = {}) ```

Figure3 网页外观

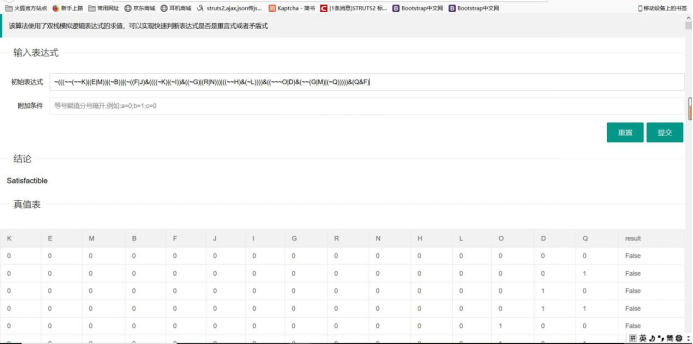
Figure4 判断结果

五、程序测试

第一次进行测试时，发现输入逻辑表达式 P | P & Q 穷举出来的结果有三个False，一个True，与实际不符（正确结果应为两个False，两个True），检查发现程序没有考虑到运算符 & 和 | 之间的优先级不同，所以先算了表达式前半部分，相当于是计算了（P | P）& Q 的结果。更正后自定义了各个符号对应的优先级，在符号出入栈时增加了比较优先级的步骤，再次进行测试。
为了避免人工构造逻辑表达式产生的局限性，我们编写了一段程序，随机生成了5000条表达式，保证了测试的覆盖完整性，提高了测试效率。生成的部分测试用例如图所示：

Figure5 测试用例

人工验证结果难免疏漏，且想要人工验证5000条结果必定耗时巨大。为了更好的验证结果的正确性，我们选用了事先写好的两段不同的程序运行上述的5000条测试用例，再将两者的结果进行比对，结果完全一致。以下是其中一个程序的部分运行结果，及两边结果的比对：

Figure6 程序运行结果

Figure7 结果比对

六、总结

该程序运用了 python语言对数据的存储结构和算法进行描述，实现了命题逻辑公式的类型判断。设输入的逻辑表达式的长度为m，其中有n个变元，则算法时间复杂度为T(n)=O(2^n)，两个堆栈的长度不超过m，空间复杂度为O(m)。该程序的优势在于代码简洁清晰，空间复杂度低，缺点在于算法时间复杂度没有得到很好的改善，仍有待优化。这次的实践要求我们结合所学，根据实际问题合理地选择相应的存储结构，并设计出有效算法，较之前的理论课来说更具有挑战性。从选题到查找资料、确定思路，从源代码的完成、调试、修改、完善到撰写报告，我们加深了对算法与数据结构概念的理解，强化了面向对象的程序设计理念，培养了综合运用所学知识处理实际问题的能力。实践过程中，我们经过查找参考资料、技术手册和撰写文档，进一步培养了软件工程师的综合素质；而通过验证自己设计的算法的正确性，我们学会有效利用基本调试方法，迅速找出程序代码中的错误并且修改。这次实践还让我们复习到了离散数学的相关知识，通过不断探寻改进更优解、写出简洁优美的算法，我们更为直观的体会到了算法之美。