聚类算法及部分介绍
1. K-menas聚类
- kmeans.py
-
kmeans-dbscan.ipynb
聚类概念: 无监督学习:无标签 聚类:相似的东西分到一组 难点:如何评估(没有目标值比较),如何调参(没有标准答案)
K-means算法: - K值:要得到簇的个数,需要指定 - 质心:均值,即向量各维取平均即可 - 距离的度量:常用欧几里得距离和余弦相似度(先标准化) - 优化目标:min(sum1,k:(sum(dis(ci,x)^2)) 每个样本点到簇中心点的距离之和最短
-
工作流程:
> 1.随机初始化K个点
2.算样本中各个点到这K个点的距离,与距离最近者归为一类,共K类
3.找出这K类中心点(质心:各维平均值)的位置
4.重复第二步,直到计算得出的新中心点与原中心点的位置一样,结束
- 优点:简单,快速,适合常规数据集
- 劣势:K值难确定,复杂度与样本呈线性关系,很难发现任意形状的簇
k-means迭代可视化:https://www.naftaliharris.com/blog/visualizing-k-means-clustering/
2. DBscan聚类
- DBscan聚类.py
- DBscan聚类2.py
-
DBscan聚类3.py
dbscan(Density-Based Spatial Clustering of Applications with Noise)算法:
- 核心对象:若某个点的密度达到算法设定的阈值则其为核心点*即r领域内点的数量不小于minPts)
- 领域的距离阈值:设定的半径r
- 直接密度可达:若某个点p在点q的r领域内,且q是核心点则p-q直接密度可达
- 密度可达:若有一个点的序列q0,q1,...qk,对任意qi-qi-1是直接密度可达的,则称q0到qk密度可达,这实际上是直接密度可达的‘传播'.
- 密度相连:若从某核心点P出发,点q和点k都是密度可达的,则称点q和点k是密度相连的
- 边界点:属于某一个类的非核心点,不能发展下线了
-
噪声点(离群点):不属于任何一个类簇的点,从任何一个核心点出发都是密度不可达的
-
工作流程:参数D:输入数据集 参数r:指定半径 MinPts:密度阈值 > 1.标记所有对象为unvisited
2.随机选择一个unvisted对象p
3.标记p为visited
4.如果p的r邻域至少有MinPts个对象,执行第五步,否则执行第6步
5.创建一个新簇C,并把p添加到C;令N为p的r邻域中的对象集合;遍历N中每个点p,如果点p是unvisited,标记p为visited;如果p的r邻域至少有MinPts个对象,把这些对象添加到N;如果p还不是任何簇的成员,把p添加到C
6.标记p为噪声
7.重复执行步骤2,直到没有标记为unvisited对象 -
参数选择:半径r:可以根据K距离设定;找突变点
K距离:给定数据集P={p(i);i=0,1,..n},计算点p(i)到集合D的子集S中所有点之间的距离,距离按照从小到大的顺序排序,d(k)就被称为k-距离 MinPts:k-距离中k的值,一般取的小一些,多次尝试
- 优势:不需要指定簇的个数
可以发现任意形状的簇
擅长找到离群点(检测任务)
两个参数就够了- 劣势:高维数据有些困难(可以做降维) 参数难以选择(参数对结果的影响比较大) sklearn中效率很慢(数据削减策略)
dbscan可视化:https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/
- 注:若找离群点epsilon和minPoints可以小一些
3. AP聚类
- AP聚类.py
-
sklearn_AP.py
https://www.cnblogs.com/zhangyafei/p/10630688.html
4. LPA聚类
-
LPA.py
标签传播聚类算法, 典型的半监督学习算法
- 核心思想:相似的数据应该具有相同的标签,构建节点间的相似性矩阵(边的权重)
5. 谱聚类算法
-
spectrual_clustering.py
核心思想:构建样本点的图,切分图,使得子图内权重最大,子图间权重最小
6. meanshift聚类算法
-
meanshify.py
核心思想:
- 寻找核密度极值点并作为簇的质心,然后根据最近邻原则将样本点赋予质心
7. 高斯混合模型+EM算法
-
Gmm_em.py
核心思想: 以alpha(k)的概率选择第k个高斯模型,再以该高斯模型概率分布产生数据。其中alpha(k)就是隐变量
i、K-MEANS 算法
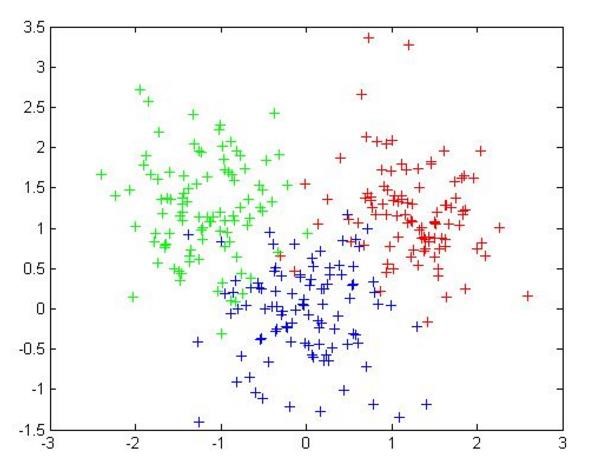
聚类概念 :
- 无监督问题:我们手里没有标签了
- 聚类:相似的东西分到一组
- 难点:如何评估,如何调参
基本概念:
- 要得到簇的个数,需要指定 K 值
- 质心:均值,即向量各维取平均即可
- 距离的度量:常用欧几里得距离和余弦相似度(先标准化)
- 优化目标:
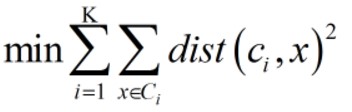
K-MEANS 算法工作流程:
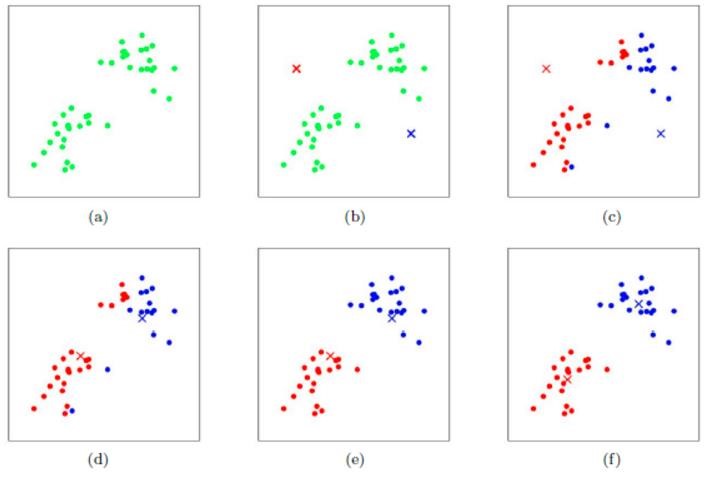
优势:
- 简单,快速,适合常规数据集
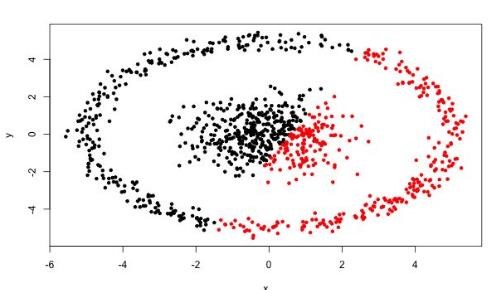
劣势:
- K 值难确定
- 复杂度与样本呈线性关系
- 很难发现任意形状的簇
ii、DBSCAN 算法
基本概念:(Density-Based Spatial Clustering of Applications with Noise)
- 核心对象:若某个点的密度达到算法设定的阈值则其为核心点。
- (即 r 邻域内点的数量不小于 minPts)-邻域的距离阈值:设定的半径 r 直接密度可达:若某点 p 在点 q 的 r 邻域内,且 q 是核心点则 p-q 直接密度可达。
- 密度可达:若有一个点的序列 q0、q1、…qk,对任意 qi-qi-1 是直接密度可达的
- ,则称从 q0 到 qk 密度可达,这实际上是直接密度可达的“传播”。
基本概念:
- 密度相连:若从某核心点 p 出发,点 q 和点 k 都是密度可达的
- ,则称点 q 和点 k 是密度相连的。
- 边界点:属于某一个类的非核心点,不能发展下线了 直接密度可达:若某点 p 在点 q 的 r 邻域内,且 q 是核心点则 p-q 直接密度可达。
- 噪声点:不属于任何一个类簇的点,从任何一个核心点出发都是密度不可达的
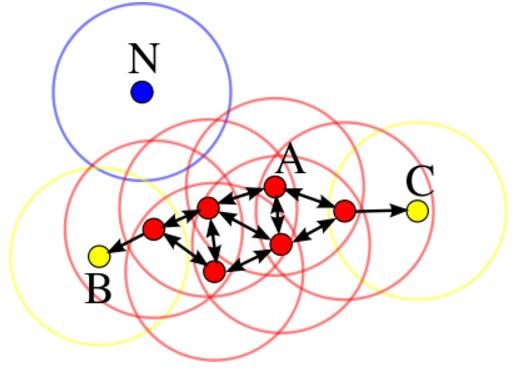
工作流程:
- 参数 D:输入数据集
- 参数:指定半径
- MinPts:密度阈值

参数选择:
- 半径,可以根据 K 距离来设定:找突变点
K距离:给定数据集P= {p(i); i=0,1,…n},计算点P(i)到集合D的子集S中所有点之间的距离,距离按照从小到大的顺序排序,d(k)就被称为k-距离。
- MinPts: k-距离中 k 的值,一般取的小一些,多次尝试
优势:
- 不需要指定簇个数
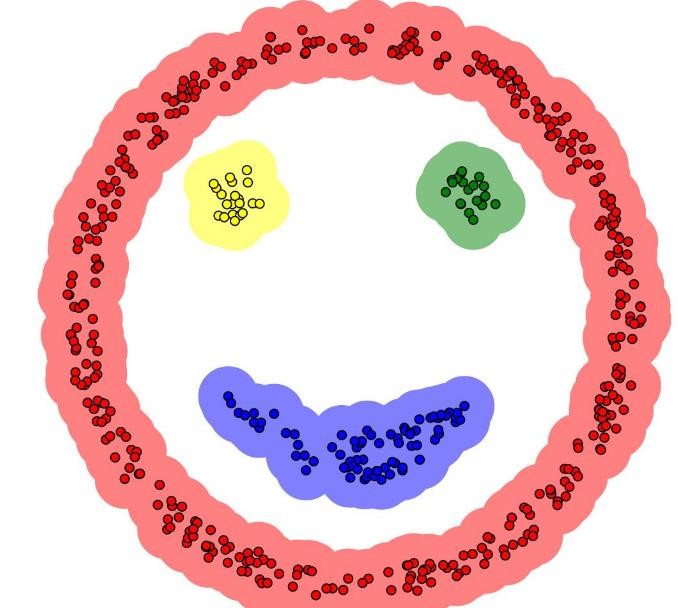
- 可以发现任意形状的簇
- 擅长找到离群点(检测任务)
- 两个参数就够了
劣势:
- 高维数据有些困难(可以做降维)
- 参数难以选择(参数对结果的影响非常大)
- Sklearn 中效率很慢(数据削减策略)


参考文献
- 基于Web数据挖掘的推荐系统算法研究(河北工程大学·冯立娟)
- 基于文本挖掘的视频标签生成及视频分类研究(上海交通大学·吴雨希)
- 基于文本聚类的垂直搜索引擎系统设计与实现(北京工业大学·陈迪阳)
- 实时数据流自适应聚类及演化分析方法研究(苏州大学·夏月)
- 基于Web使用挖掘的在线报名推荐系统的研究与实现(电子科技大学·王玥)
- 基于聚类与加权矩阵分解的推荐算法研究(山东理工大学·郭蕊)
- 基于文本聚类的垂直搜索引擎系统设计与实现(北京工业大学·陈迪阳)
- 基于K-Means的分布式文本聚类系统的设计与实现(西安电子科技大学·马婵媛)
- 基于用户兴趣的个性化信息推荐系统(西华大学·沈杰峰)
- 基于文本聚类的垂直搜索引擎系统设计与实现(北京工业大学·陈迪阳)
- 融合用户属性、兴趣度和信任度的模糊C均值聚类推荐技术的研究与实践(北京工业大学·王凯旋)
- 主题模型对多域数据的挖掘和应用(上海交通大学·陈晓宇)
- 基于聚类的电子商务推荐系统研究(华东师范大学·夏冬)
- 基于矩阵分解与PSO协同过滤的推荐算法研究及应用(中央民族大学·潘海川)
- 基于AP聚类算法的推荐系统研究(河北大学·于润杰)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:代码助手 ,原文地址:https://m.bishedaima.com/yuanma/35689.html