一、实验报告

内容（名称）：社会力模型仿真

院（系）名称	计算机学院
专业名称	计算机科学与技术
指导教师	宋晓
学号	18373584
姓名	甘天淳

二、实验目的

应用社会力模型，仿真模拟单房间疏散场景下的人员流动情况，熟悉社会力模型的基本方程和相关的路径规划算法。在此基础上进行多次仿真，分析障碍物摆放位置和人员密度对总疏散时间和平均疏散时间的影响，并对现实情况进行拟合，提出指导性意见。

三、数学模型描述

3.1 模型基本框架

社会力模型是一种以牛顿力学为理论基础，假设行人受到社会力作用产生加速度从而运动的模型。在该模型中，行人同时受到三种作用力的影响，即驱动力、人与人之间的作用力、人与障碍物之间的作用力，这三种作用力产生的合力作用于该行人，产生一个加速度，驱动行人运动。其中，驱动力是该个体对自己施加的社会力，体现了其在主观意识的影响下移动到目的地的需求；人与人之间的作用力是周围其他个体对该个体施加的社会力，体现了其尽量与他人保持一定距离的需求；人与障碍物之间的作用力是障碍物（或墙壁）对该个体施加的社会力，体现了其与障碍物保持一定距离的需求。

社会力模型的主要方程如下：

其中，

3.2 模型细节扩充

在基本框架的基础上，对模型细节做以下扩充及解释：

本实验中，选取图书馆单一房间的疏散情形为仿真场景，房间大小为x，仅存在单一出口且其在房间右侧，房间内有四个书架，大小分别为x，x。，房间构造例图如下：

图 1 房间构造例图

全过程中均将人员当做圆看待，其半径（即肩宽的一半）服从均匀分布，疏散开始时刻，人员在房间内随机分布（不存在人员互相重叠或与墙壁重叠的情况），社会力模型公式中各常量取值、各变量取值范围如下：

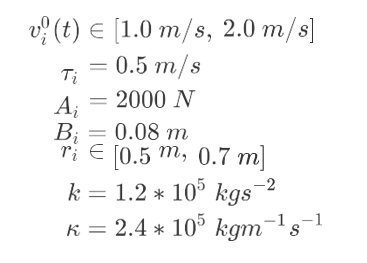
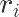
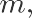
四、编程实现与调试过程

本实验中，使用Python编写面向对象的程序，其接受初始时刻人员总数量、人员最大移动速度desired_speed作为输入参数，随机生成人员初始位置，在逐步推进时间的同时计算各人员收到的社会力及对应的加速度，更新其位置并显示在GUI上，除此之外，实时显示当前时间及房间中剩余人数，仿真结束后生成密度图。源代码的部分重要函数将以附录形式呈现，以下分三部分对代码实现与运行结果做出解释。

4.1 数据结构与组织形式

采用面向对象的程序构造方式，首先介绍仿真有关各类（由于篇幅限制略去方法的具体实现，仅以注释形式给出重要方法的解释）：

二维向量：用以描述二维平面中的力、速度、位置、方向等信息。

圆形：用以描述场景中的人员信息。

```python class Circle:

Attributes:

def init (self, x, y, vx, vy, mass, scene=None) def get_radius(self) def distance_to(self, other) # 计算与参数other的距离

根据other的类型（Circle，或墙或障碍物）分别计算

return: 距离向量

def is_intersect(self, other) def ped_repulsive_force(self) # 计算行人与其他行人间的排斥力

使用公式:

f_i = ∑(j)f_ij 结果

f_ij = A * e^((r_ij - d_ij) / B) * n_ij # r_ij = r_i + r_j 半径之和

d_ij = ||r_i - r_j|| 圆心距离

n_ij = (r_i - r_j) / d_ij 单位方向向量

return: 其他行人们对此人的合力f_i

def wall_repulsive_force(s)

```

盒子：用以描述矩形墙壁与矩形障碍物信息。

```python class Box:

Attributes:

p1:

p2: 矩形对角线上的两个点的坐标。

def init (self, x1, y1, x2, y2) def scale(self, factor) def is_intersect(self, other) def is_in(self, pos) def center(self) def width(self) def height(self) ```

场景：用以描述场景信息。

4.2 仿真主要函数解释

程序依次进行初始化、仿真、输出结果三个步骤，每个步骤中的主要函数解释如下：

初始化场景 ：依次向场景中添加墙壁、障碍物、生成不互相重叠且不与墙壁障碍物重叠的若干人

员，构成初始时刻场景，并将其显示在上，具体代码及解释如下：

```python def get_scene(person_num=10): scene = Scene() Scene.scale_factor = 36 scene.border = Vector2D(15.0, 15.0) # 设置场景大小 scene.boxes = [] scene.boxes.append(Box(0.0, 0.0, 10.0, 1.0)) scene.boxes.append(Box(0.0, 1.0, 1.0, 14.0)) scene.boxes.append(Box(0.0, 14.0, 10.0, 15.0)) scene.boxes.append(Box(10.0, 0.0, 11.0, 7.0)) scene.boxes.append(Box(10.0, 8.0, 11.0, 15.0)) # 设置墙壁 scene.boxes.append(Box(3.0, 2.0, 4.5, 6.0)) scene.boxes.append(Box(6.5, 2.0, 8.0, 6.0)) scene.boxes.append(Box(3.0, 9.5, 4.5, 13.0)) scene.boxes.append(Box(6.5, 9.5, 8.0, 13.0)) # 设置障碍物 scene.peds = [] for i in range(person_num): # 随机生成人员初始位置 ped = None num_tried = 0 while not is_valid(scene, ped): # 判断是否有重叠情况存在 ped = Circle(random.uniform(1, 10), random.uniform(1, 14), 0.5, 0.5, 80) num_tried += 1 if (num_tried >= 100): print("人数太多，找不到空位啦.实际人数: %d" % len(scene.peds)) break if num_tried >= 100: break scene.peds.append(ped) scene.dests = [] scene.dests.append(Box(11.0, 0.0, 15.0, 15.0)) # 设置目的地（即出口） return scene

```

开始仿真 ：此函数被绑定到的开始仿真按钮上，是程序的入口函数，具体代码及解释如下：

```python def begin_simulate(self):

steps_per_frame = 12

steps_cnt = 0

while self.scene.peds_arrived() != len(self.peds): # 循环直至所有人均离开

steps_cnt += 1

self.timeNow = self.timeNow + TIME_STEP # 更新当前仿真时间

self.timeNowStr.set("%.4f" % self.timeNow) # 更新当前剩余人数

self.remainPeople.set(len(self.peds) - self.scene.peds_arrived())

try:

self.scene.update() # 更新场景

except IndexError:

print("IndexError\n\n")

exit(0)

if steps_cnt < steps_per_frame:

continue

steps_cnt = 0

i= 0

for ped in self.peds:

= ped[0].pos.get_x()

= ped[0].pos.get_y()

= ped[0].get_radius()

self.canvas.coords(ped[1], (x - r, y - r, x + r, y + r))

if self.pre_peds:

pre_x = self.pre_pedsi.pos.get_x()

pre_y = self.pre_pedsi.pos.get_y()

self.canvas.create_line(x, y, pre_x, pre_y, fill=self.get_color(i + 10)) # 绘制移动路径

i+= 1

```

记录速度——密度 ：在仿真过程中推进时间时记录下特定区域的人数与其中人员的速度，以供仿真结束后生成速度——密度图。

路径搜索算法 ：本实验中采用A 算法作为图论最短路算法，以下给出A 算法具体步骤如下：

算法的具体内容与解释。

算法具体步骤如下：

把起点加入 open list 。
重复如下过程：
遍历 open list ，查找 F 值最小的节点，把它作为当前要处理的节点。
把这个节点移到 close list 。
对当前方格的 8 个相邻方格的每一个方格？
- 如果它是不可抵达的或者它在 close list 中，忽略它。否则，做如下操作。
- 如果它不在 open list 中，把它加入 open list ，并且把当前方格设置为它的父亲，记录该方格的 F ， G 和 H 值。
- 如果它已经在 open list 中，检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好，用 G 值作参考。更小的 G 值表示这是更好的路径。如果是这样，把它的父亲设置为当前方格，并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话，改变后你可能需要重新排序。
停止，当你
- 把终点加入到了 open list 中，此时路径已经找到了，或者
- 查找终点失败，并且 open list 是空的，此时没有路径。
保存路径。从终点开始，每个方格沿着父节点移动直至起点，这就是所得的最终路径。

一个用A*算法搜索最短路径的例图如下：

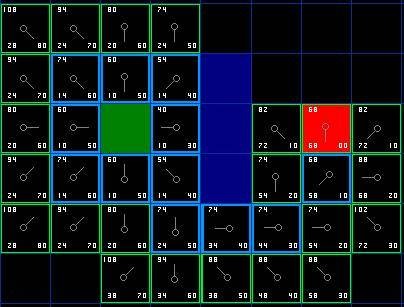
图 2 A*算法寻路过程例图

本实验中，距离主要通过以下式子产生：

其中，表示从起点沿着产生的路径移动到网格上指定方格的移动花费，表示从网格上当前方格移动到终点的预估移动花费，本实验中值采用曼哈顿方法，其计算当前格到目标格之间水平与垂直方格的数量和而忽略对角线方向，是对剩余距离的一个估算。通过这个式子可以选择下一步的方向作为社会力的驱动力部分。

由于篇幅限制，此部分完整源代码请参见附录 1：路径搜索算法源代码。

4.3 仿真结果与解释

该程序完成了仿真的基本功能并实现了实时显示房间内剩余人数、实时显示人员具体路径等附加功能。以初始时刻房间内人数为的输入条件为例进行仿真，仿真开始前（图 3），仿真进行中（图 4），仿真结束后（图 5），实时显示路径的仿真进行中（图 6），实时显示路径的仿真结束后（图 7）的程序界面截图分别如下所示：

图 3 仿真开始前

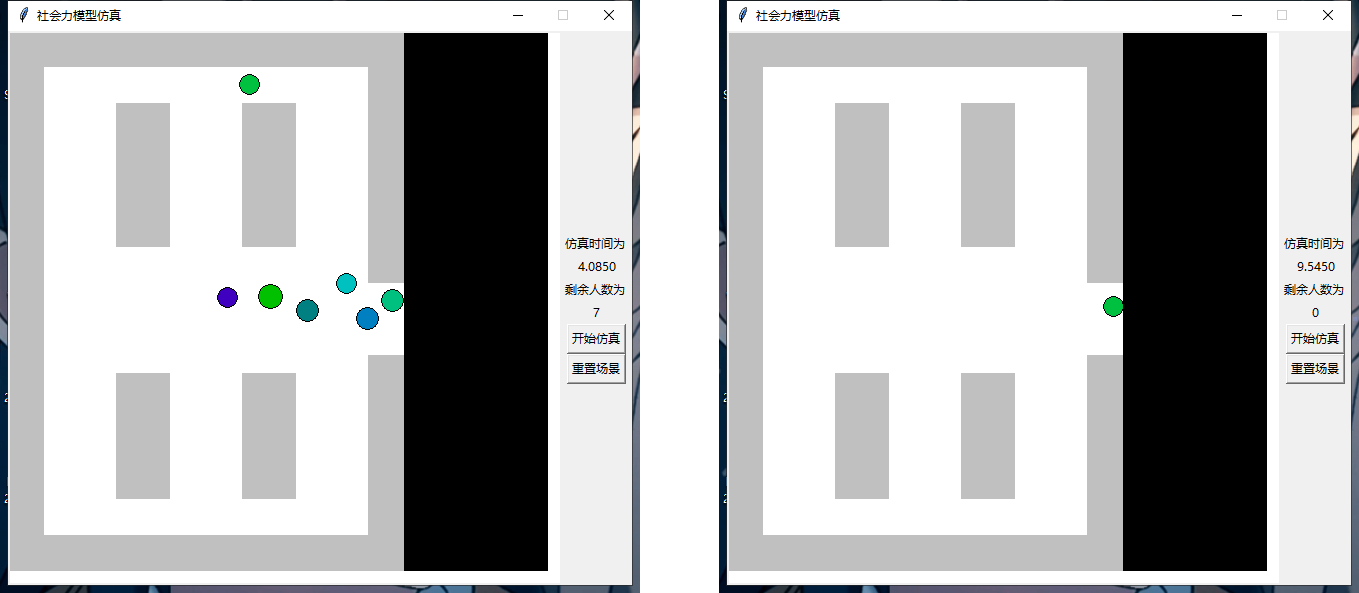
图 4 不带路径的仿真进行中图 5 不带路径的仿真结束后

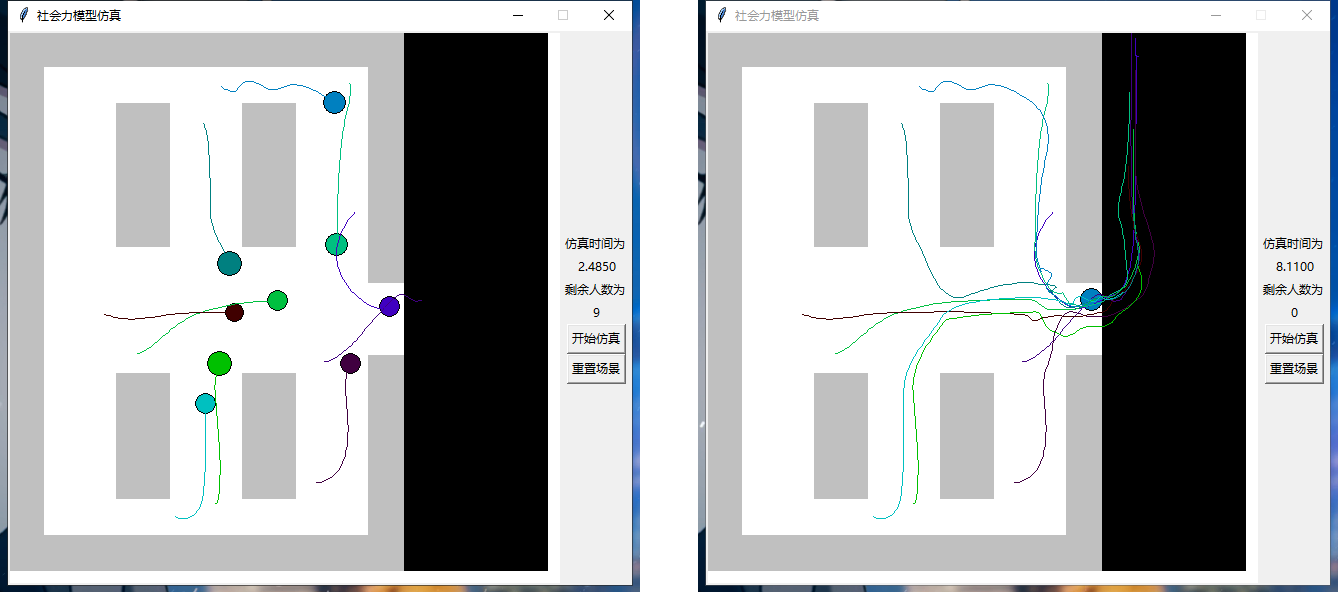
图 6 带路径的仿真进行中图 7 带路径的仿真结束后

图 8 速度—密度表与速度—密度图

由图中可以看出，区域内人流密度较小时随着人流密度的增加平均速度略微增加，人流密度继续增大时平均速度开始减小，且减小趋势趋于剧烈，当人流密度到达一定阈值时平均速度趋于稳定在一个较低的水平。结合社会力模型基本方程，并与现实相联系，图像呈此趋势的可能原因是密度较小时人仅受驱动力作用，速度达不到最大速度，密度略微增加时并不会阻塞人员前行的路线，而其后的人流会对其施加一个向前的社会力，造成平均速度略微增加，体现为正向驱动作用，与现实情况也相符。密度继续增加时若出口处已到达最大通行效率则其后人流会聚集在出口处造成平均速度大幅下降，且这种情况随密度增加而愈加严重，平均速度大幅减少，直至区域内密度稳定且所有人速度相似且均较低，达到此阈值后继续增大密度则对平均速度没有太大影响，此时速度很大程度上仅依赖于出口宽度，即出口处通行效率，与现实情况符合也较好，充分说明了仿真具有良好的现实意义，也从侧面印证了社会力模型的合理性。

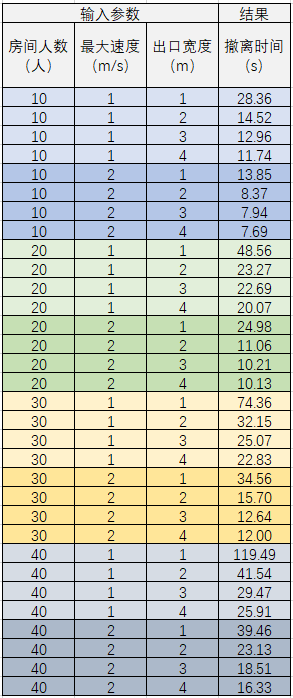
图 9 多次仿真结果表

将得到的多组数据绘制三维图像，如下所示：

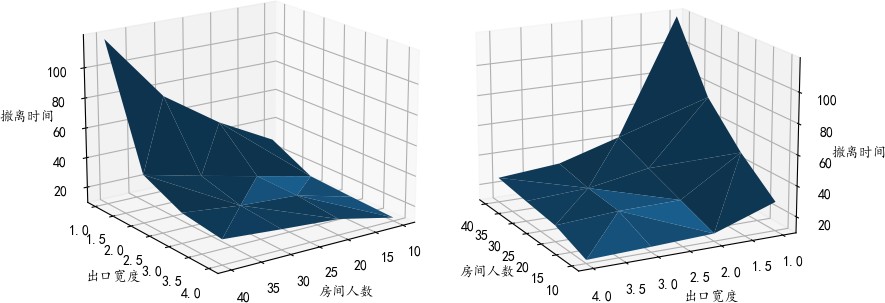
图 10 两种视角下的撤离时间与输入参数的关系图（最大速度为 1m/s）

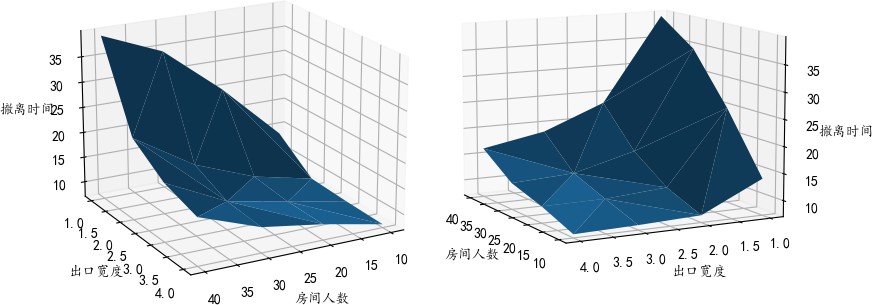
图 11 两种视角下的撤离时间与输入参数的关系图（最大速度为 2m/s）

分析以上仿真结果和图像的特点并做可能的解释如下：

总体而言，初始时刻房间内人数越少，人员最大移动速度越大，出口宽度越大，撤离所需时间越短，反之则均越低。
固定人员最大移动速度和出口宽度不变，仅改变初始时刻房间内人数，撤离时间随人数的减少而近似线性减少，且在人数减少到一定程度时趋于不变。其可能原因是人数较多时效率瓶颈在于出口处通行效率低，由于出口处通过效率一定，则总撤离时间线性减少，而人数较少时出口不会聚集较大人流，撤离时间与最远人员从初始点到达出口所需时间强相关。
固定人员最大速度和初始时刻房间内人员数量不变，仅改变出口宽度，撤离时间随出口宽度增加而近似指数减小，但在出口宽度达到一定长度时趋于不变。其原因可能是出口宽度较小时容易在出口处积累大量人流，造成通行效率较低，增大出口宽度可以显著减轻此情况的程度，而出口宽度增大到一定程度后每一时刻到达出口的人员都能直接通过出口，通行效率不再上升，因此总撤离时间趋于不变。
固定初始时刻房间内人员数量与出口宽度不变，仅改变人员最大移动速度，撤离时间在出口宽度足够长时随人员速度减少而近似线性增加，在出口宽度较小时严重延长。其原因可能是出口宽度足够时所有人走过相同路程情况下随速度不同时间近似线性变化，出口宽度较小时容易形成人流在出口处积累，此时较慢的速度会严重延长出口通过效率，造成总撤离时间大幅延长。
通过观察仿真过程中具体人流分布可以看出，出口宽度越小，越容易出现出口处形成倒三角形人流并造成通行效率大幅下降的情况，如下图 8 所示，在此基础上若倒三角形两侧人员质量相似则会出现没有人可以通过出口的情形出现（即互不相让），造成仿真异常，这也是社会力模型仿真的不足之处之一，如下图 9 所示。

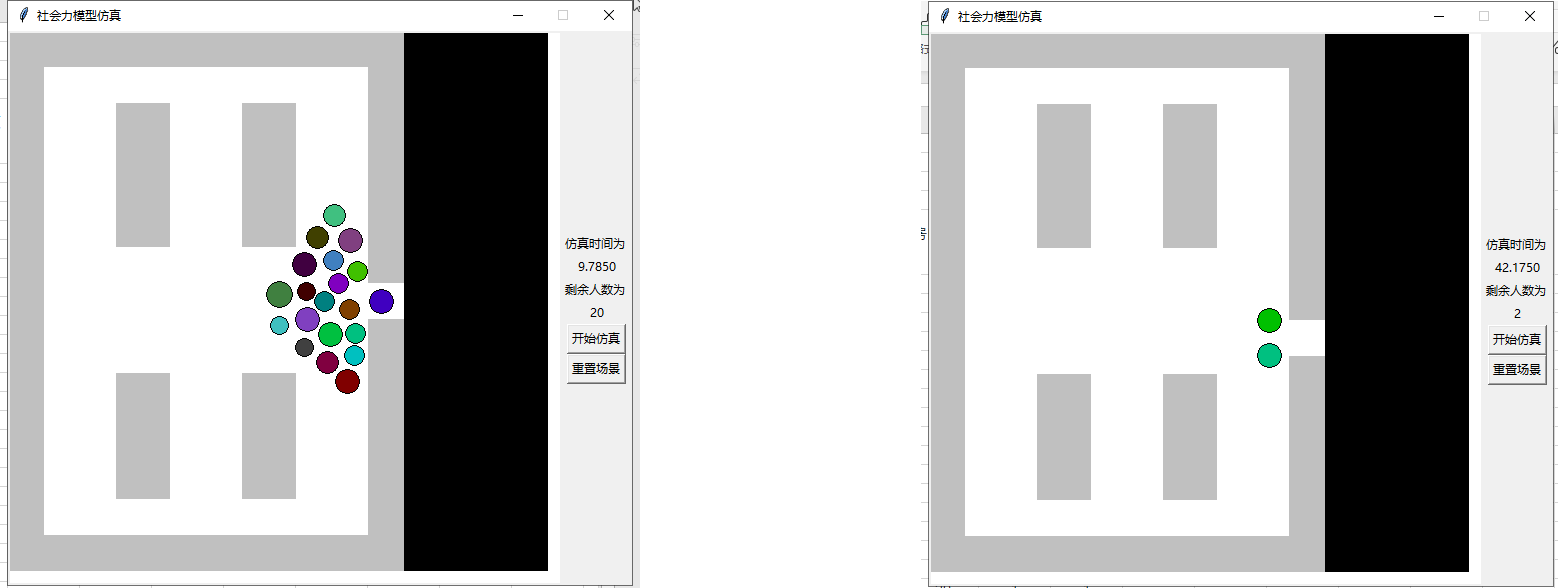
图 12 出口宽度较小时形成的倒三角形人流图 13 均无法通过出口的情形

五、与现实的联系

由上述仿真结果可以看出，增大出口宽度，增大人员最大速度，减小初始时刻人员数量均可以缩短总撤离时间，因此从缩短意外情况发生时撤离时间的考虑对博物馆/图书馆单房间的设计提出若干建议如下：

适当拓宽出口宽度，若出口宽度一定则可以通过开启多个出口的措施实现总出口宽度的扩宽。同时，需要将出口设置在合理的位置，也可以在特定的地点设置专用出口。
限制人员密度，可以通过施行分批游览的方式将人员密度控制在一个合理的范围内，从而控制总撤离时间。
优化展品/书架等障碍物摆放位置，优化人员前进路线，使得意外情况发生时能够有序撤离。
关注老年人及残障人士，其较慢的行进速度会影响房间内整体撤离效率，故应增设专门的出口或严格控制房间内该类人员数量。

附录 1：路径搜索算法源代码

```python 1 from SFM.BasicClasses import * 2 from numpy import source 3 import pandas as pd 4 5 class Node_Elem: 6 def index (self, x, y, dist): 7 self.x = x 8 self.y = y 9 self.dist = dist 10 11 class AStarPathFinder: 12 def init (self): 13 self.open = [[]] 14 self.close = [[]] 15 self.path = [[]] 16 17 @staticmethod 18 def get_direction(scene, source, number): 19 # 寻找路径，获得下一步运动的方向 20 # scene是Scene类型，source是行人（Circle类型） 21 # return: 返回期望方向e，类型为Vector2D，要求e是单位向量e.x^2 + e.y^2 = 1 22 self.number = number 23 self.source = source 24 self.scene = scene 25 point = Node_Elem(self.source.pos.x, self.source.pos.y, 0.0) 26 new_point = self.extend_round(point) 27 return Vector2D(0, 0) 28 29 def find_path(self): 30 point = Node_Elem(self.source.pos.x, self.source.pos.y, 0.0) 31 while True: 32 self.extend_round(point) # 如果这个节点的开放列表为空，不存在路径 33 if not self.open[self.number]: 34 return # 获取F值最小的节点 35 idx ,point = self.get_best() # 找到路径，生成路径，返回 36 if self.is_target(point): 37 print("We have arrived the aim") 38 return point # 找到了下一点，就找到了方向,把此节点压入关闭列表 # 并从开放列表里删除 39 self.close[self.number].append(point) 40 del self.open[self.number][idx] 41 return point 42 43 def is_target(self, i): 44 large_x = self.scene.dests.p1.x if self.scene.dests.p1.x >= self.scene.dests.p2.x else self.scene.dests.p2.x 45 small_x = self.scene.dests.p1.x if self.scene.dests.p1.x <= self.scene.dests.p2.x else self.scene.dests.p2.x 46 large_y = self.scene.dests.p1.y if self.scene.dests.p1.y >= self.scene.dests.p2.y else self.scene.dests.p2.y 47 small_y = self.scene.dests.p1.y if self.scene.dests.p1.y <= self.scene.dests.p2.y else self.scene.dests.p2.y 48 if small_x <= i.x and i.x <= large_x: 49 if small_y <= i.y and i.y <= large_y: 50 return True 51 return False 52
53 def extend_round(self, point): 54 xs = (-1, 0, 1, -1, 1, -1, 0, 1) 55 ys = (-1, -1, -1, 0, 0, 1, 1, 1) 56 for x, y in zip(xs, ys): 57 new_x, new_y = x + point.x , y+ point.y # 表示每次向某个方向移动 58 # 无效或者不可行走区域，则勿略 59 if not self.is_valid_coord(new_x, new_y): 60 continue 61 new_point = Node_Elem(new_x, new_y, point.dist + self.get_cost(point.x, point.y, new_x, new_y)) # 如果已经在close列表中 62 if self.node_in_close(new_point): 63 continue 64 i = self.node_in_open(new_point) 65 if i != -1: # 新节点在开放表，更新距离 66 if self.open[self.number][i].dist > new_point.dist: 67 self.open[self.number][i].dist = new_point.dist 68 # 现在的路径到比以前到这个节点的路径更好~,则使用现在的路径 69 # 类似于Dijkstra算法 70 continue 71 self.open[self.number].append(new_point)# 新节点不在表中，加入开放表 72 return 73
74 def get_best(self): 75 best = None 76 bv = 1000000 77 bi = -1 78 for idx, i in enumerate(self.open[self.number]): 79 value = self.get_dist(i) 80 if value < bv: 81 best = i 82 bv = value 83 bi = idx 84 return bi, best # best即是未选中表中的距离最近的 85
86 def get_dist(self, i): 87 return i.dist + math.sqrt() 88
89 def get_cost(self, x1, y1, x2, y2): 90 if x1==x2 or y1==y2: 91 return 1.0 92 return 1.4 93
94 def node_in_close(self, node): 95 for i in self.close[self.number]: 96 if node.x == i.x and node.y==i.y: 97 return True 98 return False 99
100 def node_in_open(self, node):

```