基于 OpenCV 及 Python 的数独问题识别与求解

本人平时比较喜欢玩数独，但比较难的数独经常一做就是半个多小时。这学期选了一门”计算机视觉”课，课程最后要做一个项目，正好我就想能不能写一个程序，用手机拍个照或者截个图，放进程序里跑一下，自动就把题目识别然后解出来了，and it was so.

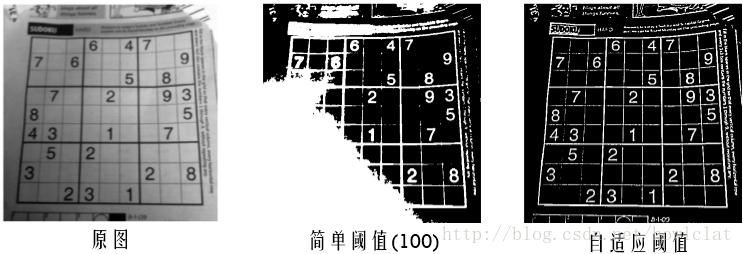
先来看一个 opencv 里自带的数独图片：

程序的最终目的就是将这种图像转化为一个矩阵或者说二维数组，来要告诉计算机在 9x9 的方格中哪个位置有数字、数字是什么，就像下面的形式：

[[0 0 0 6 0 4 7 0 0] [7 0 6 0 0 0 0 0 9] [0 0 0 0 0 5 0 8 0] [0 7 0 0 2 0 0 9 3] [8 0 0 0 0 0 0 0 5] [4 3 0 0 1 0 0 7 0] [0 5 0 2 0 0 0 0 0] [3 0 0 0 0 0 2 0 8] [0 0 2 3 0 1 0 0 0]]

在这个二维数组里，用 0 表示要填写的数字，用 1-9 表示识别出来的题目数字。

了解主要任务之后，下面就是具体的步骤了：

1. 图像预处理
2. 识别边框
3. 图像校正
4. 提取数字
5. 识别数字
6. 计算答案

这里使用的语言及版本如下，关于开发环境的配置可以参考本人 另一篇文章 ：

• Python 版本： 3.6.3 （Anaconda 3）
• OpenCV 版本： 3.3.1

第一篇文章主要讲解图像预处理部分，并给出使用 matplotlib 显示 OpenCV 图像的方法。

图像预处理

首先是使用 cv2.imread() 函数读取原图片，然后使用 cv2.cvtColor() 灰度化，因为颜色信息不重要。之后是使用滤波算法进行降噪处理，因为滤波处理对于识别效果有很大影响。常用的有均值滤波、高斯滤波、中值滤波、双边滤波等，具体使用方法可以参考 这里 。本文使用高斯滤波及中值滤波，但是滤波参数不能适用于所有情况的图像， 必须根据图像尺寸和清晰度做调整 。

python img_original = cv2.imread('./images/p1.png') img_gray = cv2.cvtColor(img_original, cv2.COLOR_BGR2GRAY) img_Blur = cv2.medianBlur(img_gray, 3) img_Blur = cv2.GaussianBlur(img_Blur, (3, 3), 0)

可以看到， Python 版本的 OpenCV 与 C++ 版本有个很大的区别，就是处理后的图像一般作为函数的返回值（之一），而 C++ 需要将原图像和处理后图像的地址作为参数传入，这是 Python 中函数可以返回多个值的特点决定的。

此图片在预处理阶段要解决的主要问题是亮度不均衡，图像左下角比较暗，如果直接进行二值化效果较差，对滤波后图像取 100 作为阈值处理得到中间的图像，左下部分图像缺失；若进行自适应阈值操作，可以得到较好的效果，但左下部分线条亦有缺失：

参考 stackflow 上一位大神的方法，以圆形作为结构化元素进行闭操作，将灰度图像除以闭操作后图像，再进行归一化。

python kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (11, 11)) close = cv2.morphologyEx(img_Blur, cv2.MORPH_CLOSE, kernel) div = np.float32(img_Blur) / close img_brightness_adjust = np.uint8(cv2.normalize(div, div, 0, 255, cv2.NORM_MINMAX))

第一句使用 cv2.getStructuringElement() 获取结构元素，可以使用椭圆、矩形、十字形三种，这里使用椭圆。第二句使用 cv2.morphologyEx() 对原图使用刚才的结构元素进行闭操作。将灰度图像除以闭操作后图像，但要先转换成 float32 类型才能除， / 运算符相当于调用 numpy 中的 divide 函数，即点除，又即每个像素点分别相除，且只保留整数部分。最后将除的结果归一化到 [0, 255] 区间内，并转换回 无符号 8 位整数（uint8） 类型。

结果如下图，效果拔群：

下一步是二值化， OpenCV 中二值化有简单阈值、自适应阈值、Otsu’s 二值化等方法，可以参考 这里 。简单阈值是一种全局性的阈值，整个图像都和这个阈值比较。而自适应阈值可以看成一种局部性的阈值，通过规定一个区域大小，比较这个点与区域大小里面像素点的平均值（或者其他特征）的大小关系确定这个像素点是属于黑或者白。这里使用自适应阈值方法，代码如下：

python img_thresh = cv2.adaptiveThreshold(img_brightness_adjust, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY_INV, 11, 7)

使用 cv2.adaptiveThreshold() 函数， 其中 cv2.ADAPTIVE_THRESH_GAUSSIAN_C 代表在小区域内阈值选取为加权和，以高斯分布确定权重。cv2.THRESH_BINARY_INV 代表二值化的结果取反，为下一步形态学处理做准备。

使用 matplotlib 显示 OpenCV 图像

Matplotlib 是 Python 中最常用的可视化工具之一，可以非常方便地创建海量类型地 2D 图表和一些基本的 3D 图表。也可以方便地显示图像。

众所周知，OpenCV 中彩色图像的像素是以 Bule Green Red 为顺序的，也就是 BGR，而普通的图像则是采用 RGB 顺序，因此要在其他地方（如 Qt、matplotlib 中）使用 OpenCV 的彩色图像，就必须转换格式。

我将使用 matplotlib 显示 OpenCV 图像的功能写成了一个函数：

python def plotImg(img, title=""): if img.ndim == 3: b, g, r = cv2.split(img) img = cv2.merge([r, g, b]) plt.imshow(img), plt.axis("off") else: plt.imshow(img, cmap='gray'), plt.axis("off") plt.title(title) plt.show()

这里先判断输入图像是不是 3 维，即彩色图，是的话进行转换，不是的话作为灰度图显示。转换代码中分割再重新组合的方法，还可以使用 img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) 。注意如果灰度图不加 cmap='gray' 这个参数，会显示为“热度图”。

当然不要忘了开头加上：

python import cv2 from matplotlib import pyplot as plt12

matplotlib 还可以像 MATLAB 里一样方便的显示多个图像，例如这里并列显示两幅图像：

python def plotImgs(img1, img2): if img1.ndim == 3: b, g, r = cv2.split(img1) img1 = cv2.merge([r, g, b]) plt.subplot(121), plt.imshow(img1), plt.axis("off") else: plt.subplot(121), plt.imshow(img1, cmap='gray'), plt.axis("off") if img2.ndim == 3: b, g, r = cv2.split(img2) img2 = cv2.merge([r, g, b]) plt.subplot(122), plt.imshow(img2), plt.axis("off") else: plt.subplot(122), plt.imshow(img2, cmap='gray'), plt.axis("off") plt.show()

其中 plt.subplot(121) 就代表一行两列图像中的第一个。

编写计算机视觉程序时可以使用上述函数将中间过程图像显示出来，方便观察与调试。例如：

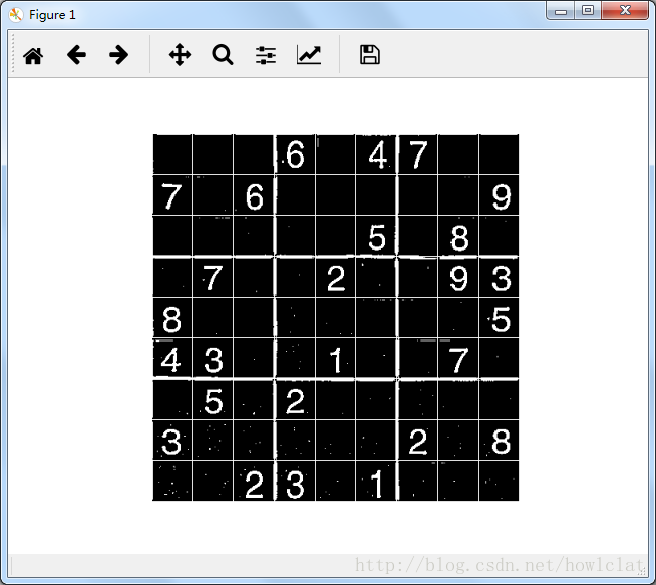
边框提取

首先进行轮廓检测。轮廓检测的原图像必须是 二值化 的图像，可以通过 threshold 或 Canny 等方法得到。同时，待检测的图像背景应为黑色而轮廓为白色，这也是上一篇中使用二值化时将图像反相的原因。

注意：在 OpenCV 3.2 版本后，函数不再对原图像进行修改而是将修改后的函数作为返回值的第一个，因此新版本中该函数有 3 个返回值 而不是旧版本的 2 个，参考 官方教程 。但在 函数说明 中，又说 3.2 版本后不再对图像进行修改（modify），据本人观察返回值中图像与原图像没有区别。

在预处理后二值图像中使用 cv2.findContours 函数检测所有的轮廓，代码如下：

python img, contours, hierarchy = cv2.findContours(img_thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

其中第二个参数选择最外层边框即可，选其他方式也可以，因为接下来会遍历找到的所有轮廓，并使用函数找到其中 面积最大 的轮廓，此轮廓即数独问题最外层边框，代码如下：

python max_area = 0 biggest_contour = None for cnt in contours: area = cv2.contourArea(cnt) if area > max_area: max_area = area biggest_contour = cnt

接下来我们要用一个掩膜（ mask ）屏蔽边框之外画面，使用 cv2.drawContours() 绘制轮廓，其中第五个参数 thickness 如果为负数则会填充轮廓内部，这里使用的 cv2.FILLED 值就等于 -1 。所以下面代码先是在全黑的图像上绘制了白色（255）的轮廓并填充轮廓内部，又用黑色（0）绘制了一次轮廓线进一步缩小掩膜，最后将掩膜与原图像进行与运算，得到纯净的数独画面。

python mask = np.zeros(img_brightness_adjust.shape, np.uint8) cv2.drawContours(mask, [biggest_contour], 0, 255, cv2.FILLED) cv2.drawContours(mask, [biggest_contour], 0, 0, 2) image_with_mask = cv2.bitwise_and(img_brightness_adjust, mask)

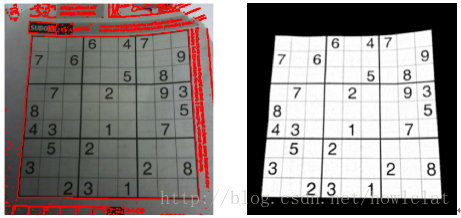
图像矫正

观察问题图像上部，存在边框线弯曲的问题，不利于下一步的数字提取。透视变换与放射变换是常用的图像校正方法，但如果将整个方框进行透视变换无法解决边框存在弯曲的问题。

将每个小方格分别进行透视变换 ，能够克服整体透视变换无法修正某一边弯曲的问题，可以将边框弯曲问题消除。主要过程是： 分别检测竖直线与水平线，取得其交点，即小方格的顶点，利用这些顶点进行透视变换。

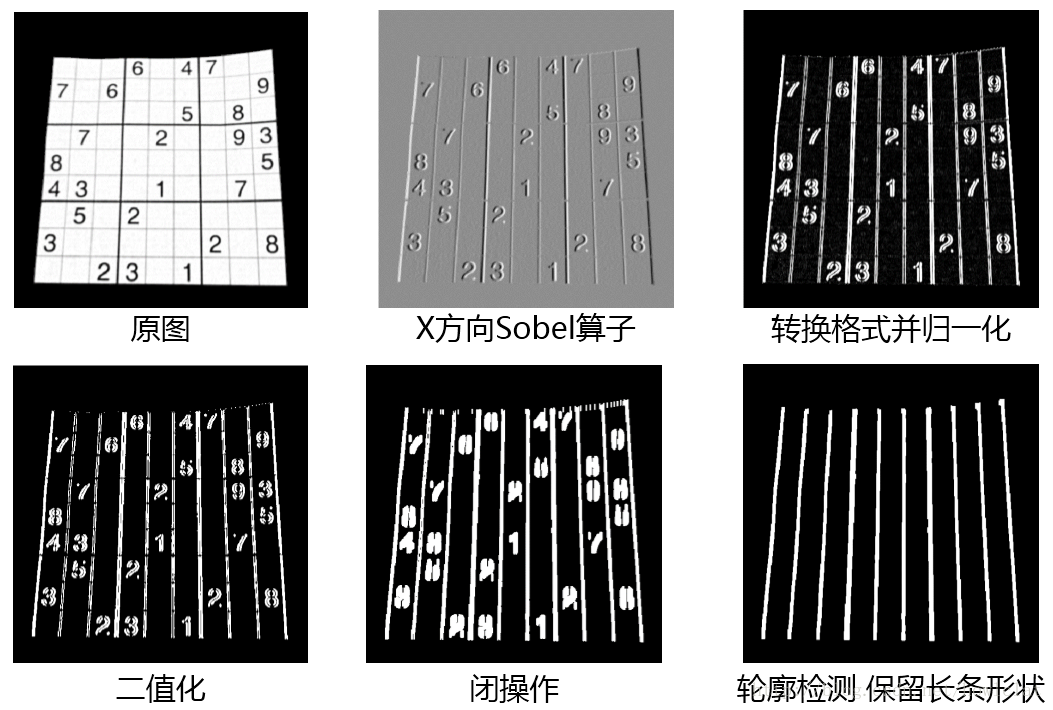
检测竖直线的关键步骤如下：

1. 利用 Sobel 算子在 x 方向检测边沿，并进行归一化和二值化；
2. 进行闭操作连接断裂的线段；
3. 检测轮廓，找出长条状的轮廓，即为竖直线。

```python dx = cv2.Sobel(image_with_mask, cv2.CV_16S, 1, 0) dx = cv2.convertScaleAbs(dx) cv2.normalize(dx, dx, 0, 255, cv2.NORM_MINMAX) ret, close = cv2.threshold(dx, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU) kernelx = cv2.getStructuringElement(cv2.MORPH_RECT, (2, 10)) close = cv2.morphologyEx(close, cv2.MORPH_DILATE, kernelx, iterations=1) binary, contour, hierarchy = cv2.findContours(close, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE) for cnt in contour: x, y, w, h = cv2.boundingRect(cnt) if h / w > 5: cv2.drawContours(close, [cnt], 0, 255, -1) else: cv2.drawContours(close, [cnt], 0, 0, -1)

close = cv2.morphologyEx(close, cv2.MORPH_CLOSE, None, iterations=2) closex = close.copy() ```

Sobel 算子中第三个和第四个参数分别为 dx、dy，这里写 1,0 就代表在 x 方向求一阶导，y 方向不求导。第二个参数 cv2.CV_16S 的解释如下，摘抄自 [这篇文章][1] 。 > 在 Sobel 函数的第二个参数这里使用了 cv2.CV_16S。因为 OpenCV 文档中对 Sobel 算子的介绍中有这么一句：“in the case of 8-bit input images it will result in truncated derivatives”。即 Sobel 函数求完导数后会有负值，还有会大于 255 的值。而原图像是 uint8，即 8 位无符号数，所以 Sobel 建立的图像位数不够，会有截断。因此要使用 16 位有符号的数据类型，即 cv2.CV_16S。 如下图中第二个所示，sobel 算子处理后会呈现灰色的图像，因此之后还需要使用 convertScaleAbs( ) 函数将图像转回原来的 uint8 类型，然后重新归一化到 0-255 范围内，并再次二值化以便进行形态学操作。 接下来使用闭操作时结构元素选择为 竖直方向较长的长方形 ，闭操作能连接断开的小线段，选择这样的结构元素这样能更好地连接竖直线，结果如第五张图所示。 最后再次使用轮廓检测，并判断所有轮廓的长宽比，保留高比宽比例大的轮廓，即为竖直线。 步骤细节如图所示：

使用同样的方法获得水平线，将水平与竖直线条进行与运算得到交叉点图像，结果为一个个小白块。

python res = cv2.bitwise_and(closex, closey)1

结果如下图所示：

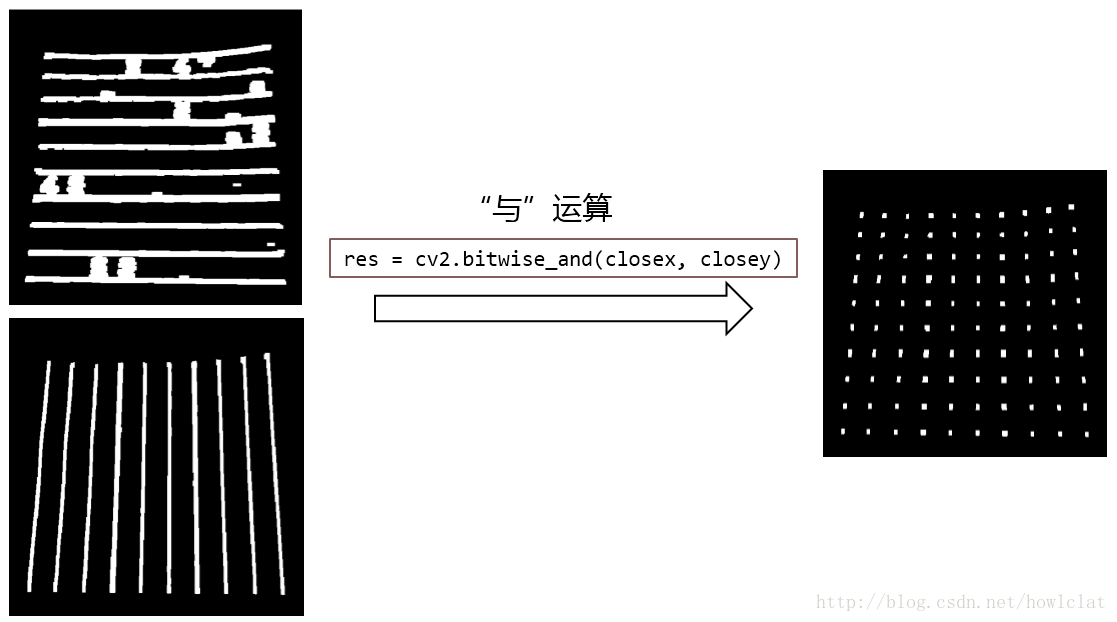
再次进行轮廓检测，检测到一个个小白块。求每个轮廓外接矩形的质心，即数独小方格的顶点。

```python img_dots = cv2.cvtColor(img_brightness_adjust, cv2.COLOR_GRAY2BGR) binary, contour, hierarchy = cv2.findContours(res, cv2.RETR_LIST, cv2.CHAIN_APPROX_SIMPLE) centroids = [] for cnt in contour: if cv2.contourArea(cnt) > 20: mom = cv2.moments(cnt) (x, y) = int(mom['m10'] / mom['m00']), int(mom['m01'] / mom['m00']) cv2.circle(img_dots, (x, y), 4, (0, 255, 0), -1) centroids.append((x, y)) centroids = np.array(centroids, dtype=np.float32) c = centroids.reshape((100, 2)) c2 = c[np.argsort(c[:, 1])]

b = np.vstack([c2[i * 10:(i + 1) * 10][np.argsort(c2[i * 10:(i + 1) * 10, 0])] for i in range(10)]) bm = b.reshape((10, 10, 2)) ```

其中求质心的用到了矩（moments）的概念，可参考 官方教程 。 最后得到的小方格顶点，如下所示：

以上步骤应该也能用 Harris 角点检测 来实现，有兴趣的可以试一下，不过内部线条比较淡而且有数字的干扰，可能需要其他的处理步骤。

最后使用小方格四个顶点将每个小方格透视变换为标准大小。

python res2 = cv2.cvtColor(img_brightness_adjust, cv2.COLOR_GRAY2BGR) output = np.zeros((450, 450, 3), np.uint8) for i, j in enumerate(b): ri = i // 10 ci = i % 10 if ci != 9 and ri != 9: src = bm[ri:ri + 2, ci:ci + 2, :].reshape((4, 2)) dst = np.array([[ci * 50, ri * 50], [(ci + 1) * 50 - 1, ri * 50], [ci * 50, (ri + 1) * 50 - 1], [(ci + 1) * 50 - 1, (ri + 1) * 50 - 1]], np.float32) retval = cv2.getPerspectiveTransform(src, dst) warp = cv2.warpPerspective(res2, retval, (450, 450)) output[ri * 50:(ri + 1) * 50 - 1, ci * 50:(ci + 1) * 50 - 1] = warp[ri * 50:(ri + 1) * 50 - 1, ci * 50:(ci + 1) * 50 - 1].copy() img_correct = cv2.cvtColor(output, cv2.COLOR_BGR2GRAY) img_puzzle = cv2.adaptiveThreshold(img_correct, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY_INV, 5, 7) img_puzzle = cv2.resize(img_puzzle, (SIZE_PUZZLE, SIZE_PUZZLE), interpolation=cv2.INTER_LINEAR)

最终结果如下图所示：

至此就得到了清晰、标准的数独问题图像，为下一步提取并识别数字做好了准备。

处理过程

数字提取的主要步骤是：将含有数字的图像，分为 9*9 即 81 个大小相同的方格，遍历这个 81 个位置，判断每个方格中是否有数字，记录数字所在位置（0~80），保存在 indexes_numbers 中，数字储存在数组 sudoku 中，主要的代码如下：

```python

识别并记录序号 (SUDOKU_SIZE = 9)

indexes_numbers = [] for i in range(SUDOKU_SIZE): for j in range(SUDOKU_SIZE): img_number = img_puzzle[i * GRID_HEIGHT:(i + 1) * GRID_HEIGHT][:, j * GRID_WIDTH:(j + 1) * GRID_WIDTH] hasNumber, sudoku[i * 9 + j, :] = extractNumber.recognize_number(img_number, i, j) if hasNumber: indexes_numbers.append(i * 9 + j) ```

Recognize_number() 函数

数字提取部分的核心函数就是 Recognize_number() ，用来判断方格中是否有数字，并存储数字，代码如下：

```python def recognize_number(im_number, x, y): """ 判断当前方格是否存在数字并存储该数字 :param im_number: 方格图像 :param x: 方格横坐标 (0~9) :param y: 方格纵坐标 (0~9) :return: 是否有数字，数字的一维数组 """ # 提取并处理方格图像 [im_number_thresh, n_active_pixels] = extract_grid(im_number)

# 条件1：非零像素大于设定的最小值
if n_active_pixels > N_MIN_ACTIVE_PIXELS:

    # 找出外接矩形
    [x_b, y_b, w, h] = find_biggest_bounding_box(im_number_thresh)

    # 计算矩形中心与方格中心距离
    cX = x_b + w // 2
    cY = y_b + h // 2
    d = np.sqrt(np.square(cX - GRID_WIDTH // 2) + np.square(cY - GRID_HEIGHT // 2))

    # 条件2: 外接矩形中心与方格中心距离足够小
    if d < GRID_WIDTH // 4:

        # 取出方格中数字
        number_roi = im_number[y_b:y_b + h, x_b:x_b + w]

        # 扩充数字图像为正方形，边长取长宽较大者
        h1, w1 = np.shape(number_roi)
        if h1 > w1:
            number = np.zeros(shape=(h1, h1))
            number[:, (h1 - w1) // 2:(h1 - w1) // 2 + w1] = number_roi
        else:
            number = np.zeros(shape=(w1, w1))
            number[(w1 - h1) // 2:(w1 - h1) // 2 + h1, :] = number_roi

        # 将数字缩放为标准大小
        number = cv2.resize(number, (NUM_WIDTH, NUM_HEIGHT), interpolation=cv2.INTER_LINEAR)
        # 二值化
        retVal, number = cv2.threshold(number, 50, 255, cv2.THRESH_BINARY)

        # 转换为1维数组并返回
        return True, number.reshape(1, NUM_WIDTH * NUM_HEIGHT)

# 没有数字，则返回全零1维数组
return False, np.zeros(shape=(1, NUM_WIDTH * NUM_HEIGHT)

```

1. 提取当前小方格的图像，并对方格图像进行预处理操作，这里用一个函数 extract_grid() 实现，具体代码见下文。函数返回 方格图像、方格二值图像、方格二值图像非零像素数 。
2. 条件 1，判断方格二值图像的非零像素数是否大于阈值，若大于阈值，认为可能存在数字。
3. 使用 find_biggest_bounding_box() 函数找出数字的外接矩形，具体代码见下文。函数返回外接矩形的 左上坐标、宽度、高度 。
4. 计算矩形中心，计算矩形中心与方格中心距离。
5. 条件 2，判断矩形中心是否离方格中心足够近，若小于阈值（方格宽度的四分之一），认为存在数字。
6. 使用 Python 的切片取出方格中数字，之后扩充数字图像为正方形，正方形边长取长宽较大者。
7. 将数字缩放为统一的标准大小。 注意！ cv2.resize() 函数在缩放二值化的图像时，默认插值方法输出不再是二值图像，若令参数 interpolation=cv2.INTER_NEAREST 输出还是二值图像，但因为像素较低效果并不好。因此涉及缩放的地方均使用原图而不是使用二值化后的图像。
8. 最后，转换为一维数组返回。

extract_grid() 函数

该函数用来提取小方格的图像，然后对其进行预处理。

```python def extract_grid(im_number): """ 将校正后图像划分为9x9的棋盘，取出小方格；二值化；去除离中心较远的像素（排除边框干扰）；统计非零像素数（判断方格中是否有数字） :param im_number: 方格图像 :param x: 方格横坐标 (0~9) :param y: 方格纵坐标 (0~9) :return: im_number_thresh: 二值化及处理后图像 n_active_pixels: 非零像素数 """

# 二值化
retVal, im_number_thresh = cv2.threshold(im_number, 150, 255, cv2.THRESH_BINARY)

# 去除离中心较远的像素点（排除边框干扰）
for i in range(im_number.shape[0]):
    for j in range(im_number.shape[1]):
        dist_center = np.sqrt(np.square(GRID_WIDTH // 2 - i) + np.square(GRID_HEIGHT // 2 - j))
        if dist_center > GRID_WIDTH // 2 - 2:
            im_number_thresh[i, j] = 0

# 统计非零像素数，以判断方格中是否有数字
n_active_pixels = cv2.countNonZero(im_number_thresh)

return [im_number_thresh, n_active_pixels]

```

1. 取出坐标为 (x,y) 的方格图像 im_number。使用 Python 中的 二维数组切片 功能，类似 OpenCV 中感兴趣区域（ROI）功能，可以方便地提取图像的某一部分，对图像进行分割。
2. 方格图像自适应二值化。
3. 由于校正后图像中有白色边框，在分割后会在每一个方格四周存在白色像素，需要去除离中心较远的像素点（排除边框干扰）。这里遍历小方格每一个像素，判断该像素与中心的距离，远于阈值的将其值设为 0，简单来说就是以方格中心为圆心画一个圆，圆内的保留，圆外的去除。
4. 使用 cv2.countNonZero() 统计现在方格中的非零像素数。
5. 将当前坐标方格图像和非零像素数返回。

find_biggest_bounding_box() 函数

该函数用来找出数字的外接矩形，输入参数为二值图像，输出为外接矩形的左上坐标和宽度、高度。

```python def find_biggest_bounding_box(im_number_thresh): """ 找出小方格中外接矩形面积最大的轮廓，返回其外接矩形参数 :param im_number_thresh: 当前方格的二值化及处理后图像 :return: 外接矩形参数（左上坐标及长和宽） """ # 轮廓检测 b, contour, hierarchy1 = cv2.findContours(im_number_thresh.copy(), cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE) # 找出外接矩形面积最大的轮廓 biggest_bound_rect = [] bound_rect_max_size = 0 for i in range(len(contour)): bound_rect = cv2.boundingRect(contour[i]) size_bound_rect = bound_rect[2] * bound_rect[3] if size_bound_rect > bound_rect_max_size: bound_rect_max_size = size_bound_rect biggest_bound_rect = bound_rect

# 将外接矩形扩大一个像素
x_b, y_b, w, h = biggest_bound_rect
x_b = x_b - 1
y_b = y_b - 1
w = w + 2
h = h + 2
return [x_b, y_b, w, h]

```

1. 对方格二值图像使用轮廓检测。
2. 遍历找到的轮廓，使用 cv2.boundingRect() 去轮廓的外接矩形， 求外接矩形面积，找出最大的面积。
3. 将外接矩形扩大一个像素，有利于识别，返回外接矩形坐标、长、宽。

效果展示

通过以上步骤，可找出哪些方格有数字，并将数字存储，如下图所示。

1->2 去除了四周的边框干扰；

2->3 找出外接矩形面积最大的轮廓并提取；

3->4 扩充为正方形，再进行缩放二值化等；

最终数字提取结果如图所示。

提取了数字，并统一成标准大小，下一步就可以进行数字识别了。事实上数字提取的过程还有一些需要改进的地方：比如从原图上提取出的数字，未缩放前为 29x29，而标准大小定义为 20x20，这样一缩放就会损失信息，有可能影响识别精度，等等。

参考文献

• 基于深度学习的小学数学辅助学习系统设计与实现（北京交通大学·王磊）
• 基于知识图谱的问答系统（华中科技大学·訚实松）
• 基于规则引擎的三角函数解题系统的设计与实现（电子科技大学·龚超）
• 基于常识推理的多模态融合算法研究（合肥工业大学·宋子杰）
• 分布式应用系统的研究与开发（武汉理工大学·廖斌）
• 基于深度学习的小学数学辅助学习系统设计与实现（北京交通大学·王磊）
• 基于结构数据的多模式智能问答消歧系统（山东大学·李华东）
• 基于.NET自定义控件的社区网站系统研究与实现（武汉理工大学·刘亚）
• 基于知识图谱的在线编程题目推荐可视分析方法（东北师范大学·杨孟茜）
• 基于深度学习的智能导学系统设计（北京交通大学·曹中）
• 基于知识图谱的在线编程题目推荐可视分析方法（东北师范大学·杨孟茜）
• 不确定性知识图谱表示学习方法研究与应用（宁夏大学·李健京）
• 基于知识图谱的学习者个性化推荐系统研究与实现（广东技术师范大学·姚俊杰）
• 基于知识图谱的深度知识追踪模型的研究（太原理工大学·张靖宇）
• 基于知识图谱的视觉问答系统设计与实现（河北科技大学·毛金莹）