CNN 模型
一、CNN 模型原理
1.1 什么是 CNN
在数字图像处理中有一个称为“边缘检测”的技术,它用到了信号的卷积操作,使用 Sobel 算子和原图像做卷积,得到的结果就是反映原图像的边界的。
受该启发,我们可以通过设计特定的卷积核,让它跟图像做卷积,就可以识别出图像中的某些特征。我们的 CNN 主要就是通过一个个的卷积核,不断地提取特征,从局部的特征到总体的特征,从而实现图像识别等功能。
而我们应该怎样去设计卷积核呢?这在数字图像处理中也是一个难题,不同的卷积核就会提取到不同的特征,而我们可能不知道应该提取哪些特征。但是结合了神经网络以后,我们就不用去考虑卷积核如何设计了,因为各个卷积核的参数都是通过神经网络自己学习得到的,这就是 CNN 的思想。
CNN 一般包含卷积层、池化层和全连接层,下面会给出解释。
1.2 为什么要用 CNN
权值共享。考虑 32 × 32 × 3 的一张 RGB 图像,即输入层有 32 32 3 = 3072 维,若隐藏层与输入层的维数一样,则输入层到隐藏层的全连接参数个数为 3072 3072 = 9,437,184 维,数目非常大,难以训练。假设使用卷积后隐藏层的每个神经元只和输入层的 5×5 个像素相连,则参数个数变为 3072 25 = 76,800,对比全连接的情况大大减少了参数个数,易于训练。
局部连接。局部连接使网络可以提取数据的局部特征,再结合池化操作实现了数据的降维,将低层次的局部特征组合成为较高层次的特征。最后再通过全连接层把卷积网络提取到的所有局部特征综合起来,得到一个全局的特征,则该全局特征既考虑了图像的各个局部细节,又考虑了图像的整体轮廓,所以有很好的识别效果。
1.3 CNN 的内在原理
以人的神经系统识别陌生人脸为引。
第一次见陌生人时,介绍人说这是张三,那么我们的神经系统一般会先记住张三的脸上的小小的细节,然后记住局部的,再记住全局印象,并且根据介绍人的说明,脑子里给这个人打上标签他叫张三。
第二次见面时,我们就会用记忆中的小小细节去和当前看到的人脸进行匹配验证,然后再用记忆中的局部特征去验证,最后就是用记忆中的全局信息去验证,通过这几个步骤后在脑海里给该脸匹配上了“张三”这个标签。
这里面的局部特征就是通过卷积层里的感受野提取得到的,全局信息就是通过全连接层把所有局部信息综合得到的。
卷积层的作用
卷积层就是对原图像作卷积操作,卷积的定义:连续形式:
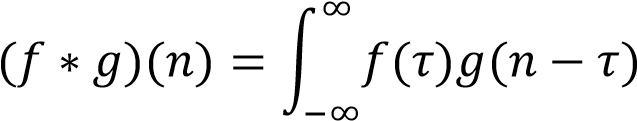
离散形式:
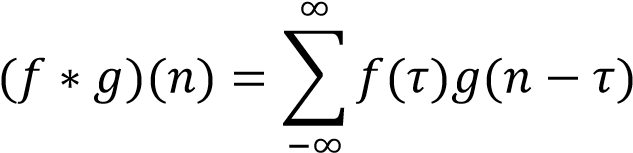
应用到图像上就是把一张图像放在另一张图像上滑动,对两张图像重叠的部分对应元素相乘求和。这两张图像分别就是原图像与卷积核。
卷积核的大小定义为感受野大小。感受野是人的神经系统里概念,表示人脑一次性捕捉信息的区域,应用在神经网络里就是卷积核的大小,它负责捕捉图像中的某一部分的信息。不同参数的卷积核相当于不同的认知策略,可以提取到图像的不同的局部特征,如边缘信息、强度中心等等。
逐层的卷积操作可以不断从原图像中提取出更高层的特征,高层的特征可以表示图像里更抽象的信息特征,逐渐增强各层得到的特征图的泛化能力。
并且逐层卷积还会使得特征图不断变小,使得训练数据量减少,可以加速训练。
1.4 padding 的作用
如上所述,经过卷积操作后图像会变小,虽然实现了对数据降维,但也不可避免地丢失了部分信息,尤其是图像边缘部分。为解决这个问题,可以采用 padding 方法,每次在卷积前,先对图像四周补若干圈像素,这样在进行卷积操作时就不会丢失边缘部分的信息,卷积得到的图像也会跟原来的一样大小。
池化层的作用
池化层类似卷积层操作,但该层是无参数的。池化主要有最大池化和平均池化两种,最大池化就是以图像的一个区域的最大值像素来代表该区域,平均池化则是以图像的一个区域的平均像素来代表该区域。
所以池化层实现了对特征图的降维,减少下一层的参数和计算量,一定程度上防止过拟合。
池化层还对特征图进行压缩,保留主要特征,具有一定程度的平移不变性、旋转不变性和尺度不变性。
平移不变性
考虑有以下原图片:
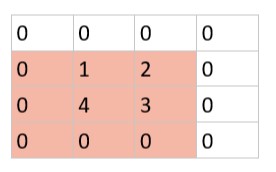
假设该图像所有像素点都右移了一位,则变成下图:
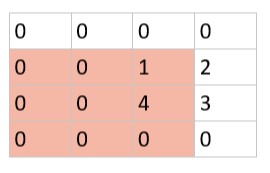
图像虽然发生了平移,像素点的位置改变了,但是如果使用大小为 3 的模板进行最大池化的话,在变化前后的图像里,红色区域的最大池化结果都是 4,说明平移变化并不影响图像红色区域的池化结果,则具有平移不变性。
旋转不变性
仍考虑上面例子里的原图,如果图像被顺时针旋转了 90°,则变成:
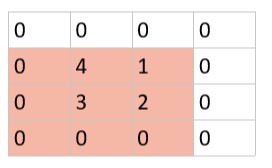
图像虽然发生了旋转,像素点的位置改变了,但红色区域的最大池化结果都是 4,说明旋转变化并不影响图像红色区域的池化结果,则具有旋转不变性。
尺度不变性
仍考虑上面的例子,假设原图在宽度上尺度增加了一倍,用 0 插值补充像素点,则图像变成:
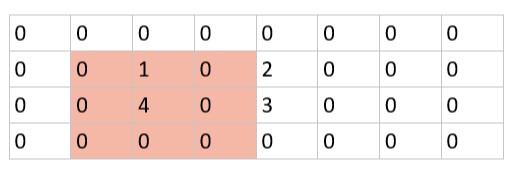
虽然图像尺度发生了变化,但是在对应位置最大池化结果仍为 4,说明尺度变化并不影响图像红色区域的池化结果,则具有尺度不变性。
二、网络结构图
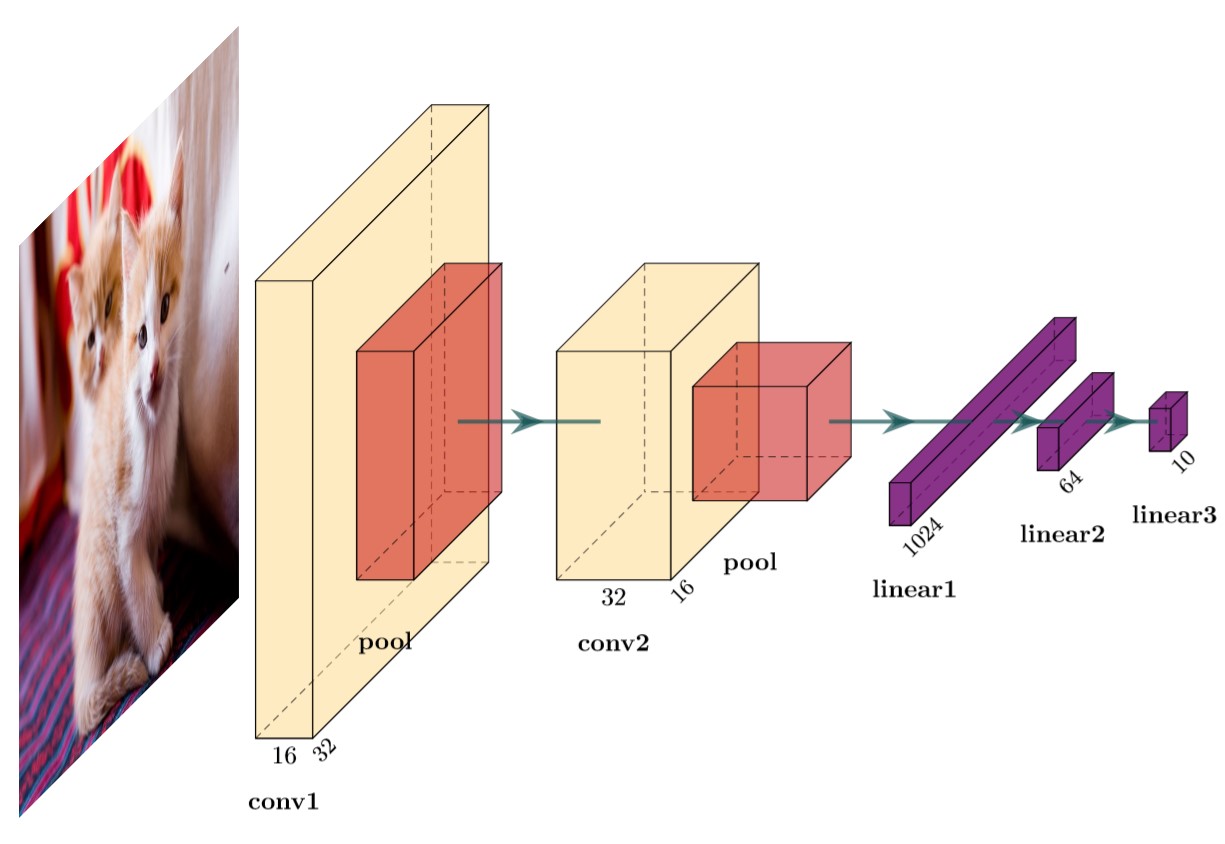
图 1,简易 CNN 结构
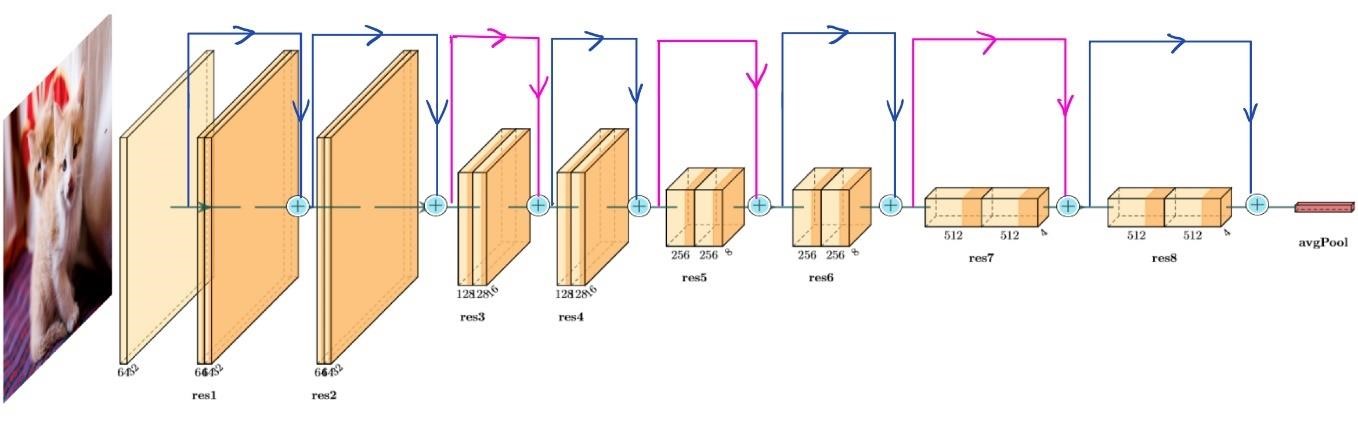
图 2,自定义的 ResNet18 结构图。其中蓝色线表示的 shortcut 代表恒等残差块,二者的大小完全一样可以直接相加;粉色线表示的卷积残差块,二者大小不相同,需要先用大小为 1 的卷积核进行卷积,对残差项进行降维,使得残差项和原始项大小一样再相加。
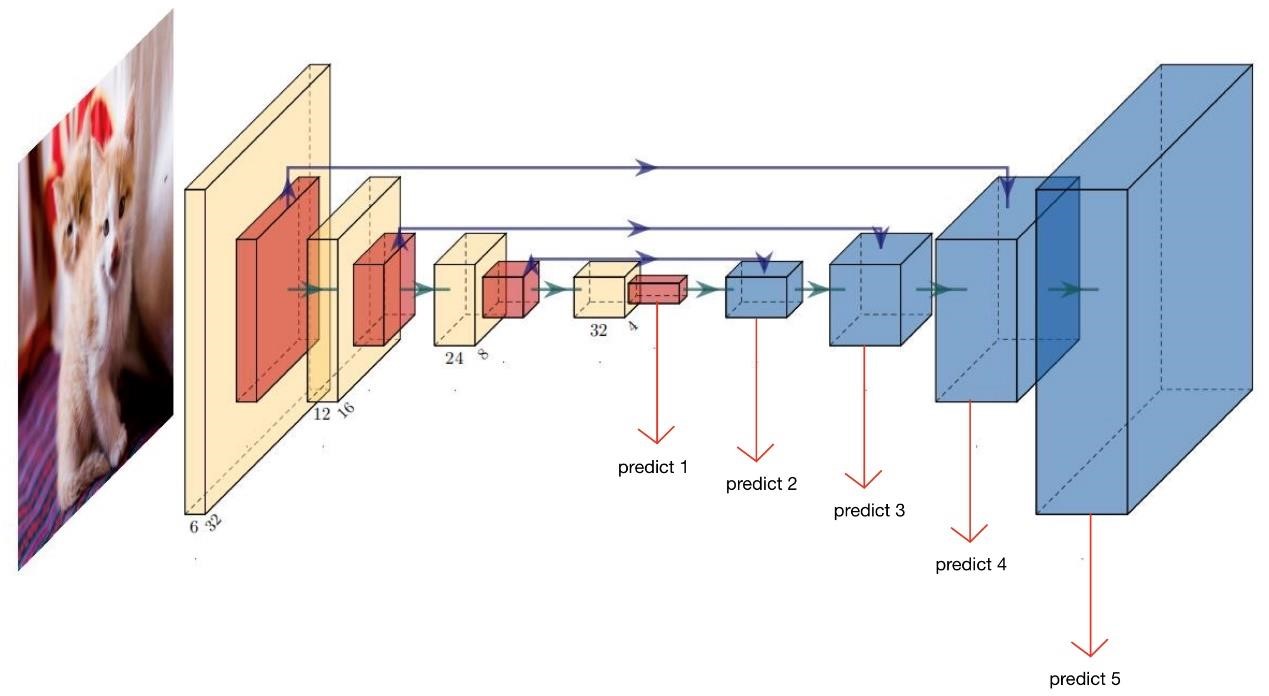
图 3,参照 FPN 自定义的网络结构图。其中蓝色方框代表对特征图上采样。图中所示的五个 predict 即对五个不同尺度的特征图进行预测,即把该特征图与一个全连接层相连得到一个十维的向量。然后再把这五个分别预测得到的结果相加起来,得到一个特征融合后的预测结果,再对该融合得到的向量所 Softmax 预测。
三、创新点
残差网络,见结果分析中的 d)
多尺度检测,见结果分析中的 e)
仿 FPN 的多尺度特征图融合、多尺度特征图预测, 见结果分析中的 f)
四、结果分析
有无 Batch Normalization[1] 使用图 1 的简易 CNN 结构作对比实验,其中一个在每个卷积层的后面都接一个 BN 层,而另一个则完全不使用 BN 层,使用同样对数据进行训练后,测试结果如下:
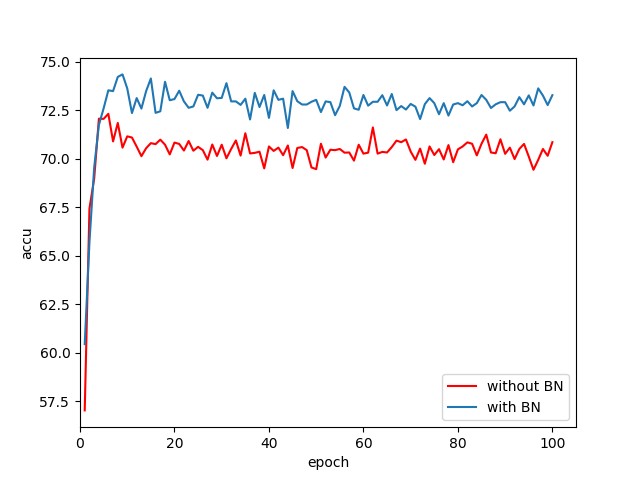
数据得出的结果显然可以看出加入了 BN 后使得网络对测试集的准确率更高了,所以可以确定我们的模型应该给每层都加上 BN。但是该结果无法表明 BN 对模型收敛速度的影响,个人猜测是因为使用的网络 backbone 过于简单所以无法体现出高层信息。
如该论文的题目所述,BN 是用了解决“Internal Covariate Shift”的,作用就是加快神经网络训练速度,并且实验发现 BN 还可以增强模型的表达效果。
论文中定义的“Internal Covariate Shift”指的是在训练过程中随着各层参数不断变化,各隐藏层的输入的分布总是在变化。一旦输入的分布发生了变化,那么该层就要重新调整参数使得该层的输出结果可以维持与标签值尽量相同。另一方面,考虑激活函数是 sigmoid 的情况,随着逐层网络训练过程,权值矩阵和偏置项很有可能使得该层的输出变得很大,这样再经过 sigmoid 函数的话就会处于饱和区域,得到的梯度很小,不利于训练。
为解决这个问题,提出了对输入数据进行“白化”操作,就是让各层的输入数据尽量符合均值为 0,方差为 1 的高斯分布,这样就可以同时解决上面所说的两个问题。给出的算法是每次对一个 mini-batch 操作,该 minibatch 里各个样本逐个分量分别计算:
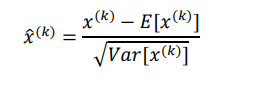
[()]为 mini-batch 中样本在第 k 维分量上的方差,[()] 为 mini-batch 中样本在第 k 维分量上的均值。
4.2.1 使用不同 batch size
使用图 1 所示的简易 CNN 结构,改变批训练的 mini-batch 大小,取 batch 的大小为 4、50 和 100,用同样的数据训练后在测试集的表现如下图:
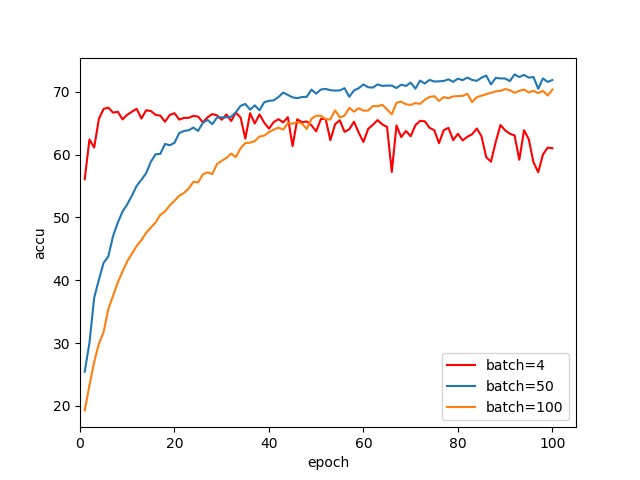
从上图显示的结果可以看出,当 batch 大小为 4 时模型收敛效果并不理想给,表现为一直在震荡,是因为 batch 太小了每次修正梯度方向都会很大的不同。Batch 大小为 50 和 100 的则表现明显变好。
在[1]中引入了 Batch Normalization,自然也讨论了 batch size 对模型效果的影响。考虑 batch size=1,即每个样本单独训练的情况,这样每次修正梯度方向都是以各个单独样本的方向,这样不同样本之间的方向很不同,修正结果难以收敛。一次性使用一个 Batch 的数据来训练,一个 Batch 里的样本的梯度可以代表整体数据集的梯度;其次,在同一个 Batch 里不同样本的计算可以并行化,加快计算速度。
所以在一定范围内增大 batch size 使得一个 Batch 更加能代表整体的梯度,并且能加快训练速度。但如果变得太大了,每个 epoch 要跑的迭代次数减少了,但在每一次迭代中,想要达到同等精确度所花费的时间也增加了,所以对参数的修正速度也更慢。且 batch size 在一定程度后,已经足以代表整体的梯度方向,继续盲目增大没有意义。
使用不同的优化器
继续使用图 1 所示的简易 CNN 结构,改变训练时使用不同的优化器,如 Adam、SGD 和 SGDM,用同样的数据训练后在测试集的表现如下图:
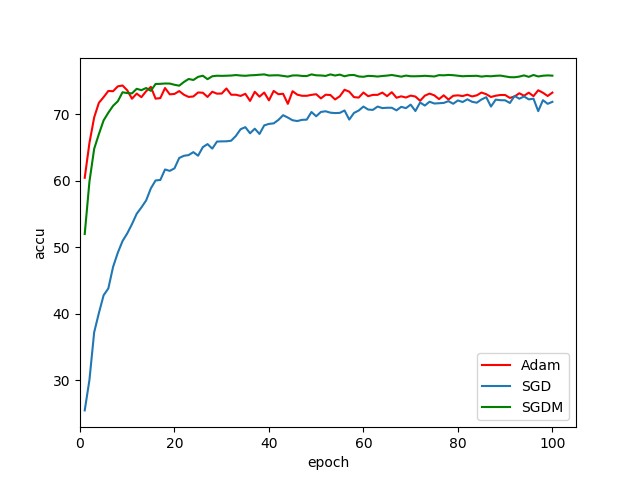
从结果可以看出来 Adam 和 SGDM 明显比 SGD 的收敛速度快,Adam 的收敛速度又比 SGDM 的要略快一点,但同时 SGDM 得出的效果又比使用 Adam 的要好。
SGD 就是随机梯度下降算法,是最简单的最优化算法,先计算目标函数关于当前参数的梯度:
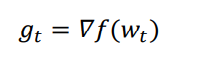
然后计算当前时刻的下降梯度:
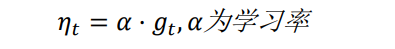
更新参数:
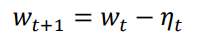
SGD 最大的缺点是下降速度慢,而且可能会在沟壑的两边持续震荡,停留在一个局部最优点。
SGDM 就是引入了“动量”概念的 SGD,梯度下降的时候,如果发现是陡坡,那就利用惯性下降快一些。SGDM 只需要在 SGD 的基础上引入一阶动量:
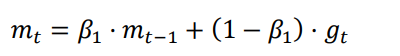
计算当前时刻的下降梯度公式改为:
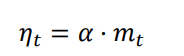
也就是说,t 时刻的下降方向,不仅由当前点的梯度方向决定,而且由此前累积的下降方向决定。1 的经验值为 0.9,这就意味着下降方向主要是此前累积的下降方向,并略微偏向当前时刻的下降方向。这样在训练初期由动量影响梯度较大,可以加快收敛速度;而在训练后期,在接近目标函数的坡谷时,由于之前动量的影响可以抑制在最优点两端震荡。
Adam 就是自适应学习率的优化器,它是在 AdaGrad 基础上的改进。
AdaGrad 引入了二阶动量的概念——该维度上,迄今为止所有梯度值的平方和:
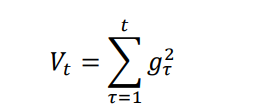
计算当前时刻的下降梯度公式改为:
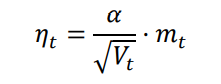
实际上就是学习率变为了
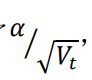 ,因此参数更新越频繁,二阶动量越大,
,因此参数更新越频繁,二阶动量越大,
学习率就越小。
AdaGrad 存在的问题是随着不断增加,学习率有可能过早减少到 0,所以出现了 AdaDelta 加入了一个时间窗口,只累积时间窗口内的二阶动量。
而 Adam 就是把 SGDM 和 AdaDelta 结合起来:
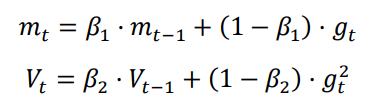
回顾上文,既然 Adam 是自适应学习率的算法,又是综合 SGDM 和 AdaGrad
的结合体,但为什么实验结果却是使用 Adam 的正确率比使用 SGDM 的要低呢?
Arxiv 上有两篇文章[2][3]谈到这个问题。[3]指出同样的一个优化问题,不同的优化算法可能会找到不同的答案,但自适应学习率的算法往往找到非常差的答案。他们通过一个特定的数据例子说明,自适应学习率算法可能会对前期出现的特征过拟合,后期才出现的特征很难纠正前期的拟合效果。[2]也是在 CIFAR-10 进行实验,发现 Adam 的收敛速度比 SGD 要快,但最终收敛的结果并没有 SGD 好。这与我们现在自己做出的结果是一致的。他们进一步实验发现,主要是后期 Adam 的学习率太低,影响了有效的收敛。他们试着对 Adam 的学习率的下界进行控制,发现效果好了很多。
使用残差网络[4]
残差网络[4]是在 2016 年提出的,主要解决了深度神经网络训练时出现的梯度消失、梯度爆炸问题,自提出以来就被应用在各种图像处理竞赛,且都有很好的成绩。我根据[4]中提供的网络参数:
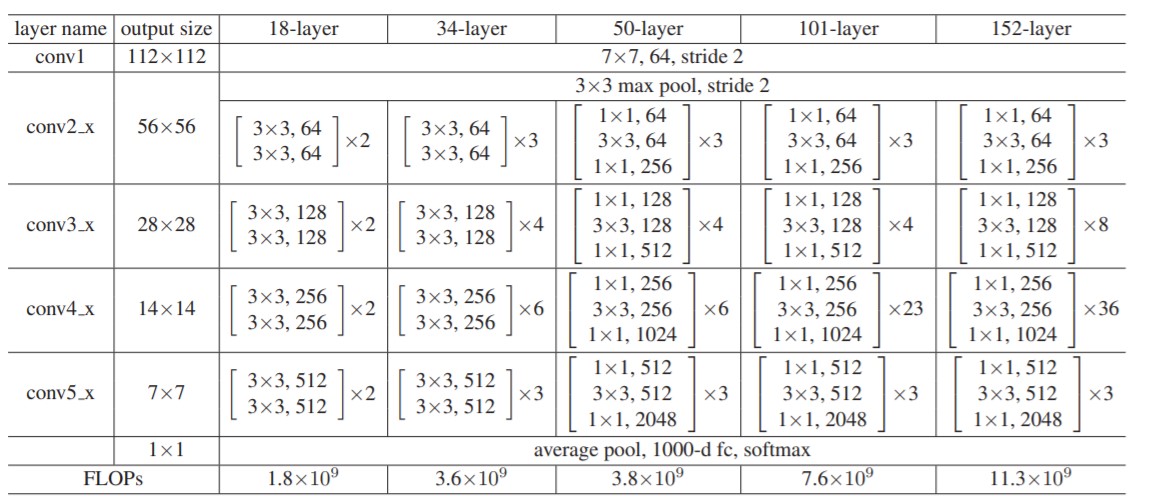
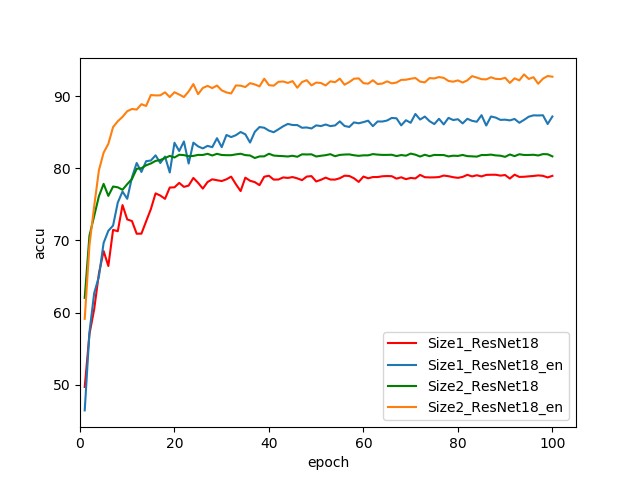
自己仿照官方的源码,改变了其中卷积核大小等参数,搭建了一个针对 32×32 输入的 ResNet18 网络,结构如网络结构图中的图 2 所示。对比用自己搭建的 ResNet18 和简易 CNN 的结果如下图:

图例中带 en 后缀的表示对训练数据进行了数据增强,如随机翻转等。可以看出使用残差网络后模型效果明显比简易的 CNN 结构好了很多。使用了数据增强又比没使用数据增强的正确率高出许多,因为数据增强可以增加训练数据的泛化性。
但回顾我们之前提到的 BN 已经使梯度稳定在正常范围了,为什么还要通过 ResNet 来避免梯度爆炸、梯度消失呢?论文[5]认为,即使 BN 过后梯度的模稳定在了正常范围内,但梯度的相关性实际上是随着层数增加持续衰减的。而经过证明,ResNet 可以有效减少这种相关性的衰减。[6]也提到过类似的现象,“由于非线性激活函数 Relu 的存在,每次输入到输出的过程都几乎是不可逆的(信息损失)。我们很难从输出反推回完整的输入。也许赋予神经网络无限可能性的“非线性”让神经网络模型走得太远,却也让它忘记了为什么出发.”[7]。
所以残差网络实际上就是要学习一个“恒等映射”,事实上,已有的神经网络很难拟合潜在的恒等映射函数 H(x) = x。但如果把网络设计为 H(x) =x,即直接把恒等映射作为网络的一部分。就可以把问题转化为学习一个残差函数 F(x) = H(x) - x.只要 F(x)=0,就构成了一个恒等映射 H(x)= x。 而且,拟合残差至少比拟合恒等映射容易得多。所以就有以下的残差块结构:
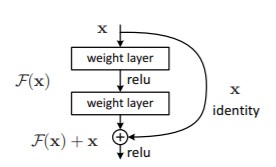
多尺度检测
因为 PyTorch 集成了 ResNet 的网络,提供的接口是针对 ImageNet 的,即 224×224 的图像,所以我们可以先对我们的数据调整到 224×224,再调用 PyTorch 提供的接口。这样可以得到改变输入尺度的对比结果:
多尺度就是对信号的不同粒度的采样,通常在不同的尺度下我们可以观察到不同的特征,从而完成不同的任务。在 CV 领域里的目标检测、实例分隔常常会用到多尺度识别的方法。通常是大尺度特征图检测大目标,小尺度特征图检测小目标。
从上图实验结果可以看出,改变了输入图像的尺度使得同样的残差网络得到的结果准确率降低了,猜测的原因是 CIFAR-10 数据集的图像都是 32×32 的,如果强行对原始图像上采样使其变成 224×224 的话,有可能会因插值不准确而丢失许多信息,所以导致分类效果变差了。
仿 FPN 的多尺度特征图融合、多尺度特征图预测接着前面多尺度检测的话题,在 CV 领域里的多尺度方法还可以应用于多尺度的特征图处理,如多尺度特征图融合、多尺度特征图预测等。以 Feature Pyramid Networks(FPN)为例:
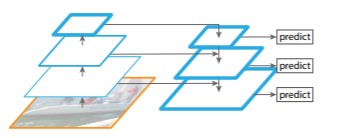
将高层的特征添加到相邻的低层组合成新的特征,每一层单独进行预测。把输入图像降维是通过卷积层实现的,而把高层的特征图上采样则是使用插值方法,如双线性插值。
使用 FPN 的方法来进行图像识别任务是因为我个人猜测可能数据集里并不是所有样本的前景图像大小都是一样的,如果存在大小不一的前景的图像,那么就相当于是尺度不一的目标,所以猜测多尺度检测的方法有可能会带来更好的效果。
使用图 1 的简易 CNN 结构,图 3 的在 CNN 基础上模仿 FPN 的改造结构实验结果如下:
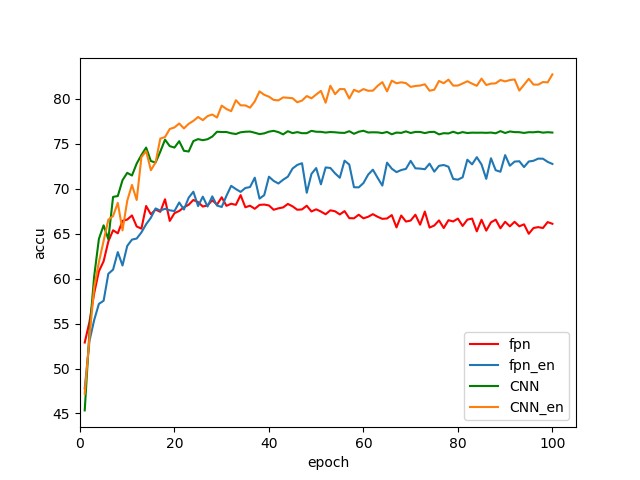
从结果可以看出,使用了多尺度融合、多尺度预测的模型效果明显变差了。原因可能是浅层的不准确预测结果影响了深层特征的预测结果,也可能是上采样插值使得特征图效果变差了。不同于目标检测中的不同尺度特征图检测不同的目标,图像分类中只有一个目标,所以不存在不同尺度特征图适用的多目标。
综合前面的多尺度的分析和仿 PFN 的结构分析,目标检测的方法确实并不适用于图像分类,把目标检测的方法移植过来反而使模型变得更差。
循环神经网络任务
实验任务及数据处理
实验任务
本次实验采用的数据集是 Semantic Textual Similarity 2012-2017 Dataset。它收集了 2012 年到 2017 年的新闻,论坛等英文预料。数据包含了的 8000 对句子已经他们获取的来源、时间和标签等信息,以及数据集中提供的这两个句子的相似度。下面从训练集中取出一行数据观察,可以看到每一项用\t 隔开,其中倒数第三列是相似度,倒数第二列和倒数第一列是我们的目标语句。
c++
main-captions MSRvid 2012test 0001 5.000 A plane is taking off. An air plane is taking off.
本次实验目标是搭建自己的网络,通过已经划分好的训练集构建并训练自己的网络,使得网络可以为这两个句子的相似度进行打分,打分区间是 0 到 5 之间, 终目标是要和数据集中提供的句子标准相似度接近。
4.3 数据预处理
在进行实验前,需要对数据进行一个预处理和清洗,我们先对数据进行一个分词,因为要从 glove 词表中提取词语的向量,如果要匹配向量,必须要保证词语完全一致包括大小写问题。但句子中的词语的首字母通常是大写,这样会在 glove 中无法找到对应的词语,因此我们需要将首字母变成小写的形式。分好词语后,因为数据中包含很多标点符号和制表符换行符等影响的信息,我们先使用正则表达式将非英文单词的组成符号去除,这里要注意有些词语是用横杠连接的,所以有些符号是不能去除的,否则会影响原来的语义。
接着,因为提供的语料中也存在很多拼写错误的情况,所以我们就去遍历 glove 词表,对每一个词语,如果不在 glove 中的话,就将它从句子中删去,同时对于存在在 glove 中的词语,我们用它对应词语向量做一个替换。
还存在一个问题就是,Lstm 模型的输入,不能接受不定长度的输入,一个矩阵一定要对齐才能作为输入进入模型,因此我们要设置一个允许的句子 长长度作为截止,超过这个长度的句子单词舍弃不要,小于这个的做一个 padding 操作来补齐,对齐了数据之后组成一个 nparray 就可以作为输入进入 Lstm,我们还要定义列表 mask 用来装每个句子原本的真实长度,作为参数传入 Lstm 训练模型中,从对应位置取出状态,就不用将 padding 的无意义的数据也加入计算影响实验效果了。
实验分析及思路
本次实验其实相当于一个有监督的学习过程,数据集中提供了句子和相似度。因为自然语言处理中不可能将文字作为神经网络的模型输入来分析,因此我们必须将词语句子转化成向量或者矩阵,才能进行神经网络的计算。因此可以想到的是,可以利用很多训练好的现成的词向量工具来训练句子的向量代表句子的语义。
我们首先可以先将句子进行分词和去噪,让句子变成一个个词语的序列。之后读入 glove 已有的词向量,用不同维度的词向量代替字符串,这样就可以得到我们的模型输入。 后我们根据数据是词语的序列的特点,我们可以想到使用循环神经网络的方法来提取特征训练我们的句向量。这里会发现有个特别的地方是,因为有两个句子,如果只有一个网络,我们没办法用相同的参数同时训练出两个不同的句向量。因此我们这里参考了 Jonas Mueller,Aditya Thyagarajan 在 2016 年发表的关于孪生 lstm 网络的论文 [Siamese Recurrent Architectures for Learning Sentence Similarity][ https://www.aaai.org/ocs/index.php/AAAI/AAAI16/paper/view/12195/12023 ]。这篇论文也是关于文本相似度的模型,它利用孪生网络共享参数来解决上述问题。
训练好句向量后,我们可以利用不同的方法来计算两个句子的相似度并进行打分。比如在自然语言处理中,解释性相对较强的在本次实验中也实验效果 好的余弦相似度。其次我们可以使用在论文
c++
[Siamese Recurrent Architectures for Learning Sentence Similarity][
https://www.aaai.org/ocs/index.php/AAAI/AAAI16/paper/view/12195/12023 ]推荐的街区距离的方法,这篇论文中提出街区距离的效果特别好。而在论文[Improved Semantic Representations From
Tree-Structured Long Short-Term Memory Networks][ https://arxiv.org/abs/1503.00075 ]中提出,将两个网络训练出来的lstm网络做差和相乘拼接后利用全连接层来训练,让网络自己来学习相似度。
后还有一个是 sts 数据集自己说明的推荐使用方法,就是用皮尔逊相关系数来计算句子相似度,个人认为可解释性不强,因为 lstm 训练出来的是一个句子向量,每一个元素都代表着这个句子的一个特征,而不是一个独立同分布的采样序列,但因为是推荐的方法,可能会有一定实验效果。
在建立好基础的模型后,就可以开始进行改进和创新了,首先是对学习率进行了调整,学习率在训练过程递减。同时还尝试了不同的 lstm 模型,比如双向的 lstm 和多层的,还使用了神经网络的方法拟合相似度,也取得了不同的实验效果。
实验基本原理
本次实验采用了孪生 lstm 网络的方法来训练句向量。
lstm 网络是对循环神经网络的一个改进, 基础的循环神经网络的原理,就是上一步中神经网络隐藏层节点的值会和下一步的输入结合在一起作为下一次的输入,这就相当于允许信息从网络的一个步骤传递到下一个步骤。
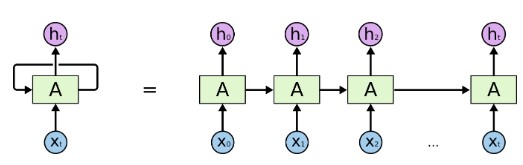
这种链的性质揭示了循环神经网络与序列和列表密切相关。它们是神经网络的自然结构,用来处理这些数据。在 RNNs 应用到各种问题上取得了令人难以置信的成功:语音识别、语言建模、翻译、图片字幕等等
但是很多时候,我们要推断一个词语,需要再前文很远的地方才能找到线索,比如说:”I lived inFrance, I worked there for many years, I…, I am now fluent in ___.”这里我们首先可以判断出应该填某种“语言”,但是究竟是哪个语言,就需要再往前找,也许很远很远,才能找到 France 这个词,这样才能确定答案是 French。
面对这样的“长距离依赖”(Long-Term Dependencies),RNN 的效果就开始变差了。虽然理论上可以通过仔细调参数在解决,但是在实践中,人们发现这个问题很难克服,即 RNN 很难学习到长距离的信息。
其实 LSTM 主要的改进之处,就是把神经网络层中对信息的处理变得更加复杂、精细了 ,可以看到 LSTM 的内部结构如下:
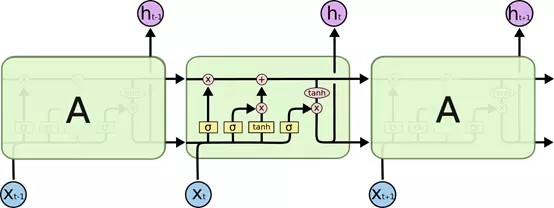
下面就一步步地分解上面的结构,逐层的理解:
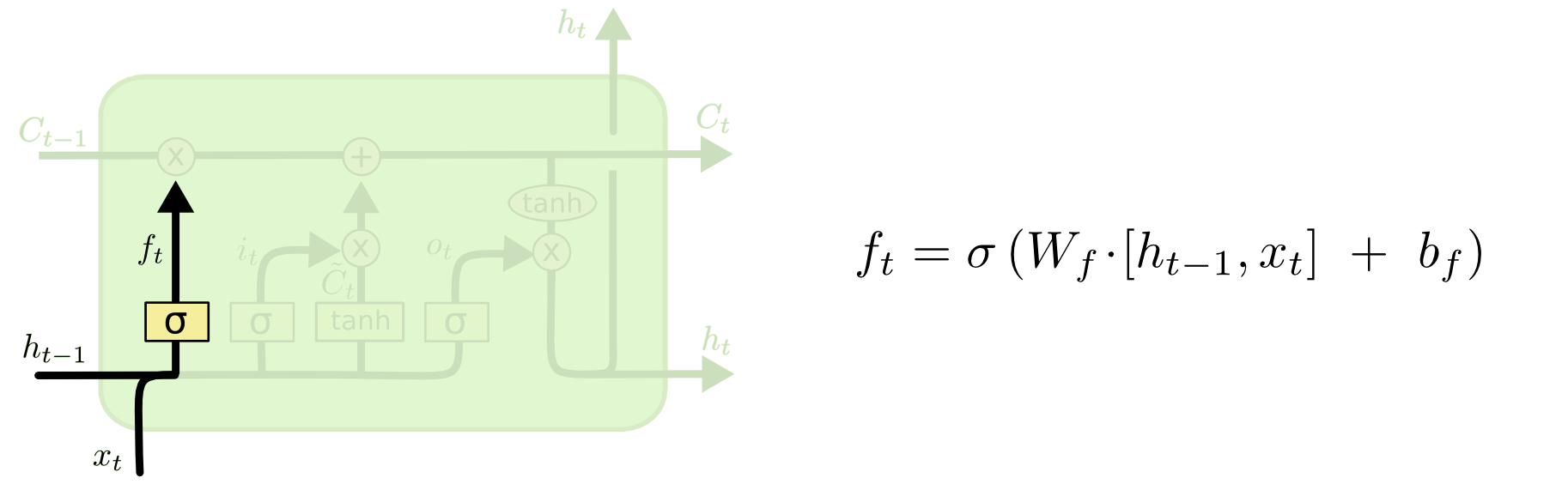
4.4 遗忘门
LSTM 的第一步是决定从细胞状态中丢弃什么信息。这个决定是由一个称为“忘记门”(遗忘门)层的 sigmoid 层做出的。它通过将 ht-1 和 xt 合在一起,并通过 sigmoid 函数并为细胞状态 Ct-1 中的每个数字输出一个介于 0 和 1 之间的数字。1 表示完全保留这个,0 表示完全去掉这个 ,中间值则表示保留的程度。这个方法为神经网络提供了一种学习的方法,就是忘记很长时间的或者相关度不高的状态,去学习到当前的状态。
4.5 输入门
上一个输出加上这一次的输入后经过 tanh 层,将信息转化为一个新的候选值,tanh 的作用就是相当于把数据规范化到-1 和 1 之间,这些就是需要更新的值。他们还要再统一经过 σ 层,这一步就相当于一个“扫描仪”,检测每个要更新的值是否需要更新,或者需要更新多少,然后将扫描的结果得到 0 到 1 的值对应乘到 tanh 层后的结果,就是 cell state 中需要更新的值了 。
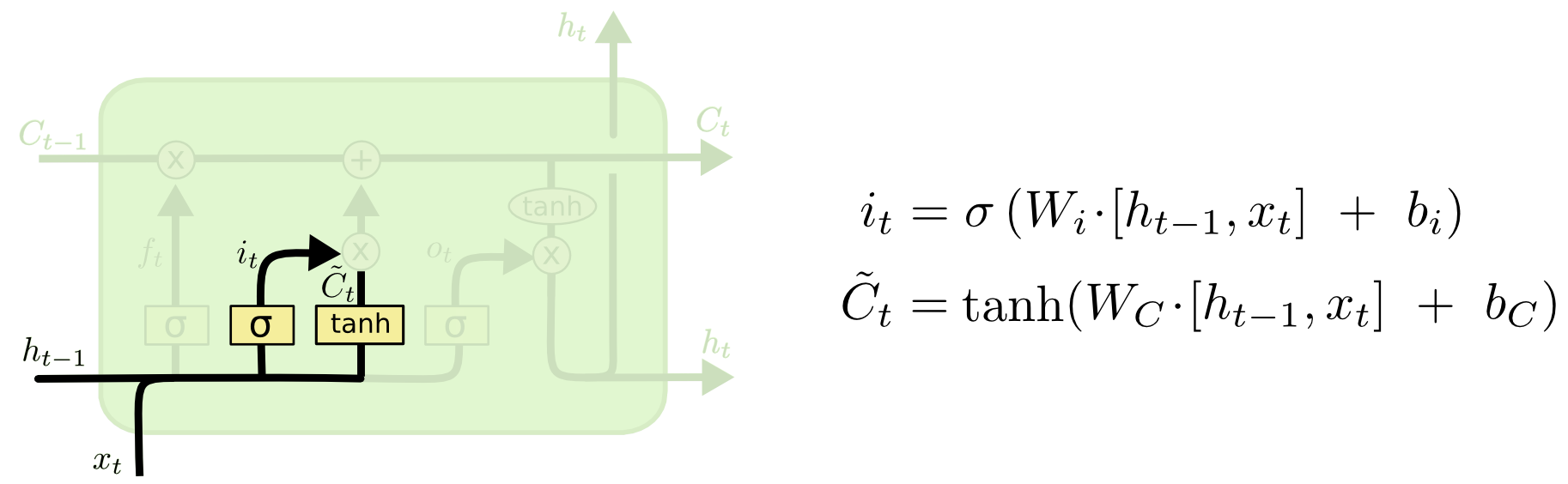
4.6 Cell state(单元状态流)
单元状态流就是下面这个水平直线,它用于“记忆”当前的状态,上面包含记忆的删除、更新。它通过三个门传过来信息,来更新单元的状态。
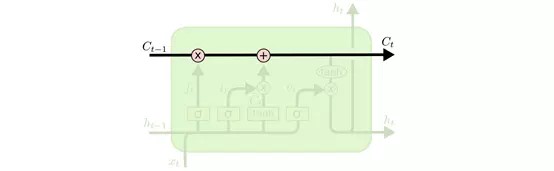
上面的两个门,“遗忘门”和“输入门”已经决定好了什么要遗忘,什么要更新保留了,现在就可以在 cell state 上执行了:
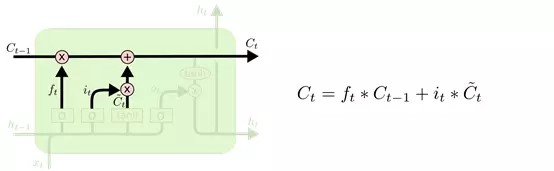
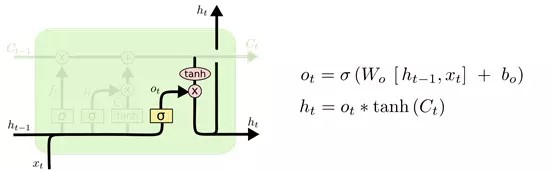
4.6.1 输出门
还是和上面一样, σ 层识别哪一部分信息要输出,乘以当前的状态 Ct(经过 tanh 处理过了),就得到了我们的输出 。
有了 lstm 网络,我们就可以训练得到句子向量。我们这里使用了孪生的 lstm 网络,也就是同时使用建立两个网络,我们将句子 a 和句子 b 分别输入到两个网络中训练,但这两个网络必须保持参数共享,也就是两个 lstm 网络在训练的时候要使用同一组参数,这样在反向传播误差的时候,就会更新同样的参数。
4.6.2 相似度
在训练完后两个目标句子的句向量后,我们需要使用一些方法求出他们之间的相似度。
余弦相似度 一种很常见而且解释性较好的方法是利用余弦距离公式。这里其实就相当于将 lstm 产生的两个输出序列,当作了这两个句子在语义空间对应的句向量。
他们之间的余弦距离,其实就相当于求两个语义空间的句子向量之间的夹角大小,越大也就表示关系越小,当两个句子方向完全相反的时候,此时相似度为 0,完全同向的时候,句子相似度为 5。
因此就需要将得分,从余弦距离的输出空间-1 到 1 映射到 0 到 5 之间,且不能改变原来的相关度排序。这是就考虑使用一个线性变换,如:
这样相当于做了一个简单的线性变换,没有改变原来相似度的排序,并且将相似度映射到了 0 到 5 区间上。
街区距离 另外一种尝试了的方法是论文 [Siamese Recurrent Architectures for Learning Sentence Similarity][ https://www.aaai.org/ocs/index.php/AAAI/AAAI16/paper/view/12195/12023 ]中使用的街区距离的
方法,我们直接用 lstm1 和 lstm2 做一个差,但街区距离并不好归一化来衡量。所以论文中就将他们的取反作为 e 的阶,然后输出的值作为相似度:
这种方法确实可以将距离转化到 0 到 1 之间的值,但在我试验过程中会发现,lstm1 和 lstm2 的差往往很大,经常都到了五百多的值,就会导致上述结果的输出值非常的小,在对损失函数使用梯度下降法时会发现刚开始模型收敛速度非常的慢,输出的相似度值一直很小,和目标相似度差距还是很大,往往训练了一段时间效果也不明显。
也考虑过用外加一些取个十分之一之类的方法让 lstm1 和 lstm2 的差值变小一点,但这样的话,模型的可解释性不高,而且让 lstm 缩小的比例并不通用,需要经常调节,且效果并没有余弦相似度更好,因此仍然选择了余弦相似度来衡量。
4.6.3 损失函数
有了每个句子对的相似度,我们可以选择距离公式来计算和目标相似度之间的距离。深度学习中有很多距离的度量方式给我们选择。本次实验我选择了下述两种常见的方法来衡量和标签值的差别
均方误差(MSE) 这个方法其实就是将两个向量做差,然后平方后再求均值。
皮尔逊相关系数 这个计算方法是提供这个数据一方要求的评测方法,就是求两个向量之间相关系数的方法:
4.6.4 网络示意图
下图是基础的 lstm 实现语义相似度的网络结构图,还有其他的改进会在创新中提到。这也是整个实验中效果 好的模型,不管是加了双向 lstm,多层 lstm,效果都没有 基础的网络效果好,分析可以猜测是这组数据因为数据量不大,语句也并不是长句,并不适合使用过于复杂的模型来拟合。如果模型过于复杂反而可能出现训练收敛缓慢,或者过拟合在验证集上表现不好的问题,而且对于有一些模型可能并不适合当前的数据,所以模型并不是越复杂越好的。
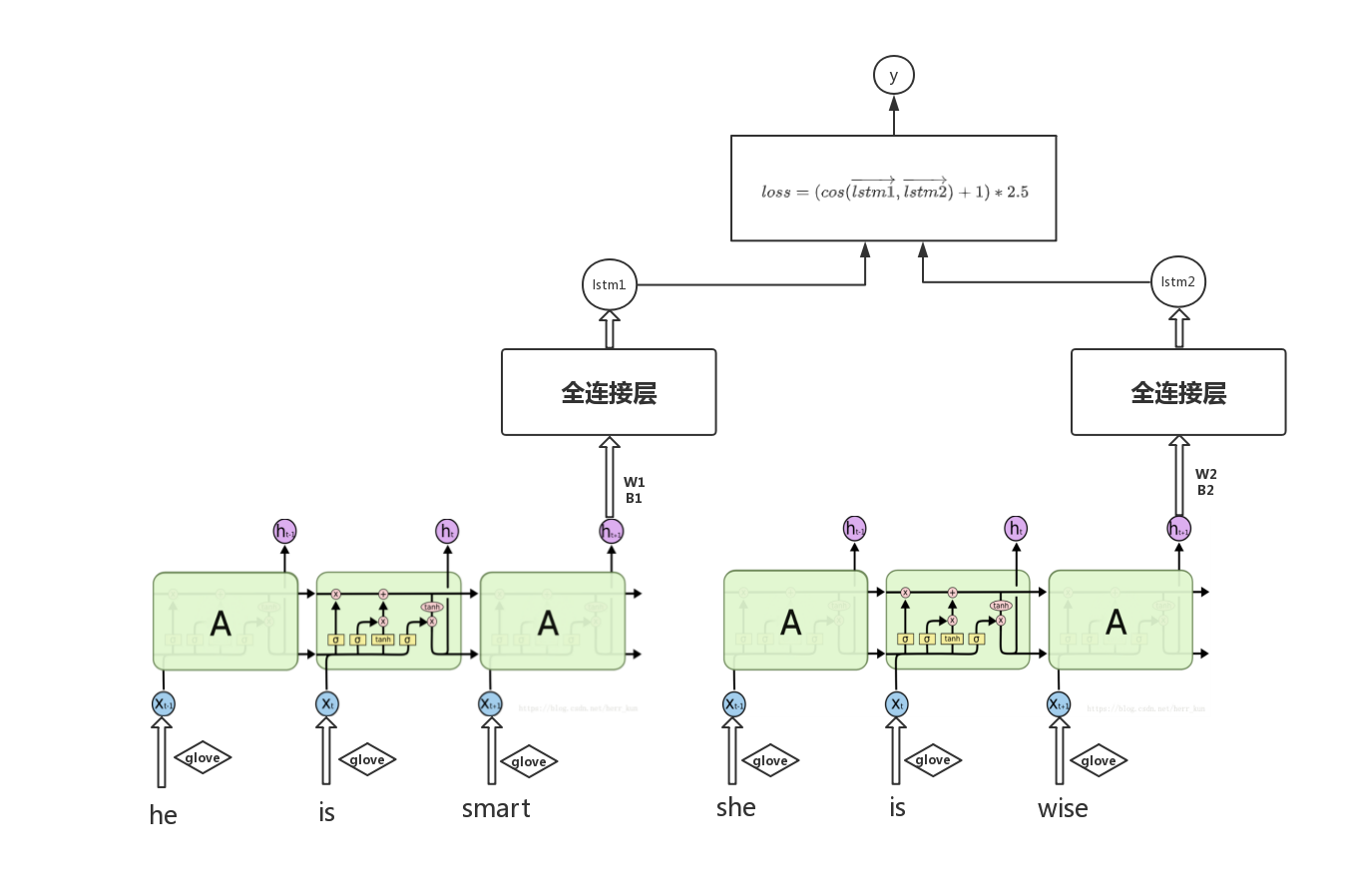
结果分析
虽然 sts 数据集的标准检测方法是用皮尔逊相似度来计算准确度,但在实验过程中,使用皮尔逊相似度的结果不是特别的突出,而且有时候会出现奇怪的波动。因此,本次实验没有采用皮尔逊相似度的度量方法,而是采用了更直观的平方误差的方法来衡量。
下面的展示是 基础的单层 lstm 和余弦距离搭配的模型。
4.6.5 调整隐藏层节点数
首先讨论在 lstm 在不同隐藏层节点下的实验效果,将 lstm 隐藏层节点从 32,64,128,256 和 512 逐步递增,运行 1500 次迭代的实验效果:

可以看到随着 lstm 隐藏层节点从 32 个开始增加,实验的 loss 有一个明显下降的变化,但当增加到 512 后,下降幅度又变小了,而且因为节点数太多,训练速度变得十分缓慢。可以得出结论,lstm 的隐藏层节点数量在合适范围的增加可以提升模型的实验效果和准确度。也可以理解成用更多的维度来表示一个句子向量,可以捕捉到句子更多的信息,这样可以更好的区别句向量,也可以更好的计算相似度。
4.7 调整 batch_size 大小
在深度学习中又不同的设置 batch_size 的方法,当数据集不大的时候, 好的方法就是: 全数据集 (Full Batch Learning ) 作为一批的输入,因为它代表着整体下降的梯度,可以 准确的用梯度下降法优化到 优情况,但问题也存在:
随着数据集的海量增长和内存限制,一次性载入所有的数据进来变得越来越不可行训练速度太慢,没办法查看更新过程 loss 下降变化和参数的变化既然 Full Batch Learning 并不适用大数据集,那每次只训练一个样本不就解决问题了,即 Batch_Size= 1。这就是在线学习(Online Learning)。线性神经元在均方误差代价函数的错误面是一个抛物
面,横截面是椭圆。对于多层神经元、非线性网络,在局部依然近似是抛物面。使用在线学习,每次修正方向以各自样本的梯度方向修正,横冲直撞各自为政,难以达到收敛。
于是 批梯度下降法(Mini-batches Learning) 就是两者折中的结果,它有很多的好处:
数据集足够充分,那么用一半(甚至少得多)的数据训练算出来的梯度与用全部数据训练出来的梯度是几乎一样的。
内存利用率提高了,大矩阵乘法的并行化效率提高跑完一次 epoch(全数据集)所需的迭代次数减少,对于相同数据量的处理速度进一步加快。于是我们可以从另外一个角度来分析,如果改变 batch_size,也就是每一次训练同时喂入的一批数据的数量,我们改变 batch_size,控制其他的属性不变,可以得到以下的实验结果:
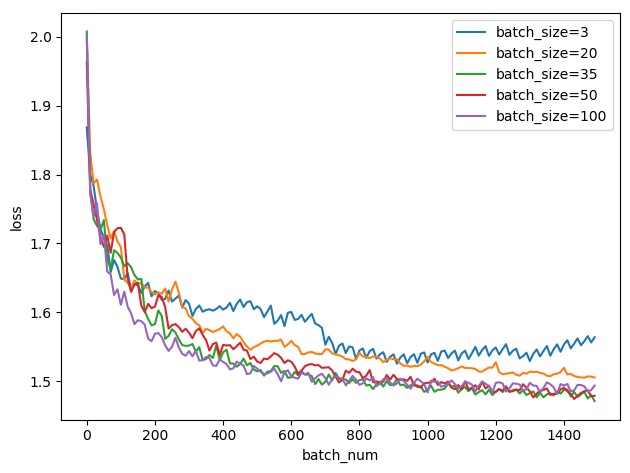
可以看到,因为这个模型对于这个数据是可以收敛的,35,50 和 100 在 1500 次 batch 后都大概收敛到相近的位置,对于可以收敛的情况,batch_size 对实验的精度不会有很明显的提升。但是可以看到, batch_size 越大,在收敛过程中的抖动会更少,蓝色在 200 到 400 次收敛的过程中波动明显 大,而红色在这个区间内波动时 小的,可见 batch_size 可以让训练更准确,向着更精准的方向前进。
这里还取了一个很极端的情况作为对照,当 batch_size 为 3 的时候可以看到,1500 次迭代后模型也无法收敛,一直在上下波动,并且波动程度很大,说明梯度没有向对的地方一直下降,而是一直在横冲直撞。
模型的相对最结果 在训练过程中达到的 优情况时当然参数为以下的时候:
| 参数 | 取值 |
|---|---|
| lstm hidden units | 512 |
| batch_size | 35 |
| n_inputs(词向量大小) | 100 |
| lr 初始学习率 | 1 |
| decay_rate 学习率衰减 | 0.96 |
| batch_num | 3000 |
| max_steps(词序列 大长度) | 65 |
在上述情况下可以达到 loss=1.42 的水平,这并不一定是这个模型在这个数据集上的 优情况,只是我在实验过程中调整参数得到的相对 优结果。通过图像可以观察得出,在迭代过程中 loss 还是一直在下降的,所以如果提高从迭代次数或者调整参数,可能可以达到更优的水平。下面就时从网络架构的角度而不是参数调整的角度进一步改进和优化模型,尝试新的网络架构,看看是否会有别的实验效果。
模型的改进与创新
神经网络模型可以有很多不同的变式,因此可以对模型进行很多不同方面的改进和对比测试得到 优的解。
学习率衰减
在神经网络的训练中,学习率是梯度下降过程中的一个重要参数,如果设置的太大,模型的训练速度会提升,但很容易出现无法到达 优点,因为学习率太大,而快到 优点的时候一下子学习过多,跳到另外一侧,然后另一侧又再跳回来,一直无法收敛。如果设置的太小,模型的训练速度和收敛速度就会特别的慢,要花费很多时间来训练而且不能达到比较好的效果,但如果运行足够长的时间理论上是能达到优点的。
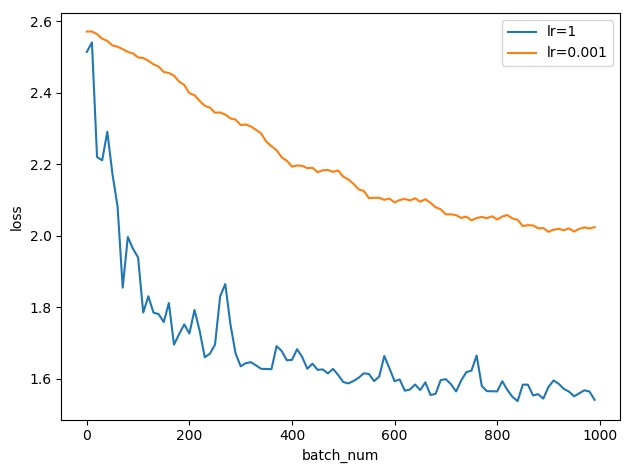
对于以上两种情况,上图展示了当学习率为 LR=1 和 LR=0.01 的不同情况下学习 的过程。其中蓝线是学习率为 1 的时候,可以看到它一开始就下降的特别快,但到后面就在 1.6 的附近上下波动,而且幅度比较大,我们就可以判断是出现了学习率过大导致不能收敛的问题。
而红线则是学习率为 0.01 的情况,准确度在一直上升且波动较小,但收敛速度慢,到 2.0 左右就十分缓慢了。
针对以上问题,我采取了学习率衰减的办法,使用 tf.train.exponential_decay 实现一个学习率的
阶级递减,其中每一定次数的 batch_num 就会下降到原来的 decay_rate 倍。就可以解决上述的问题。
双向 Lstm(bi-Lstm)
在自然语言处理中,语句中词语序列中的每个词语往往都会和它前面几个词语和后面几个词语有关联,对一些数据可能这样会让输出的预测值更为准确。我们可以看到 lstm 原论文中的的原理图:
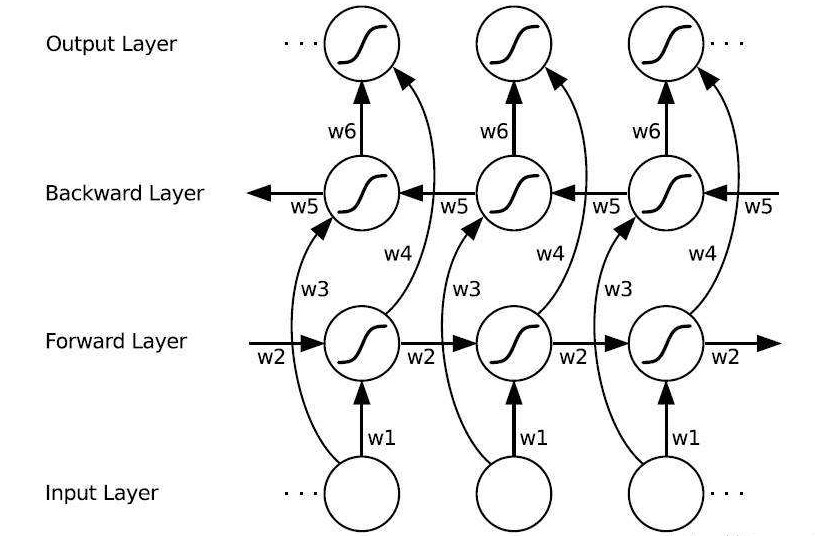
上图的每个节点其实就是上文原理部分介绍的那个 Lstm 的隐层。输入仍然按照时序输入,不过此时
Lstm 的隐层变为了两层,分别是前向和后向的 Lstm,在后项 Lstm 中,就相当于将句子倒着输入到模型中, 后我们可以分别得到前项和后项两个 Lstm 的输出结果,对于输出结果的处理我们就可以有很多不同的尝试,比如将输出结果加和,或者将输出结果使用 tf.concat 拼接在一起变成一个向量。对于两种情况,我们绘制出训练的 batch_number 和在验证集上的相似度的平方误差 loss 的函数图像:
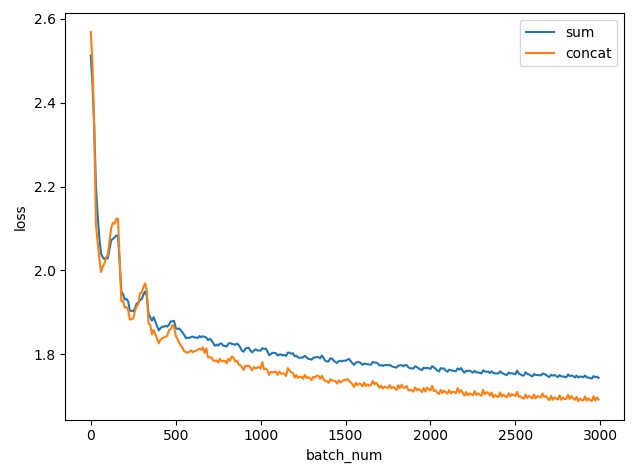
上图中蓝色线是平方误差的变化曲线,而橙色的线是拼接的方法的变化曲线。在 batch_size=35 的情况下,一共迭代 3000 次,可以看到,两条曲线都是从初始的 2.5(也就是完全没有训练的情况),损失率逐渐下降, 后蓝色线在 1.8 左右收敛,而橙色线在 1.6 左右收敛,后面随着梯度一直变缓慢,收敛速度越来越慢。
多层 Lstm 模型(Multi-Lstm)
多层的 Lstm 和单层的原理完全一样,其实就是保存下 lstm 所有 step 的隐层状态,然后再将每一步的隐藏层状态作为输入,输入到下一层的 Lstm 中,然后从 后一层 Lstm 中得到模型的输出结果,本质上还是一样的,只不过是更多的 Lstm 层的堆叠,如下图示意:
使用了多层 Lstm 后效果并不明显,经常会导致效果更差,可能是因为模型过于复杂导致收敛速度慢。如果提升迭代的次数,就会出现在训练集上的效果较好,但在验证集上的效果波动很大效果并不好,因为训练慢效果也不是很好,所以没有专门做更一步的对比实验展示。
用全连接层拟合相似度
在论文[Improved Semantic Representations From Tree-Structured Long Short-Term Memory
c++
Networks][ https://arxiv.org/abs/1503.00075 ]中,他们也是针对同一份数据集的研究。在他们的研究后发现,如果将lstm模型的输出结果直接再用减法和乘法运算后拼接在一起再次扔入全连接层,让神经网络去拟合相似度, 后套一个sigmoid函数,让输出的结果在0到5之间,然后 小化和标准的差值,可以达到更好的效果。
新增全连接层后得到的新的模型的示意图如下:
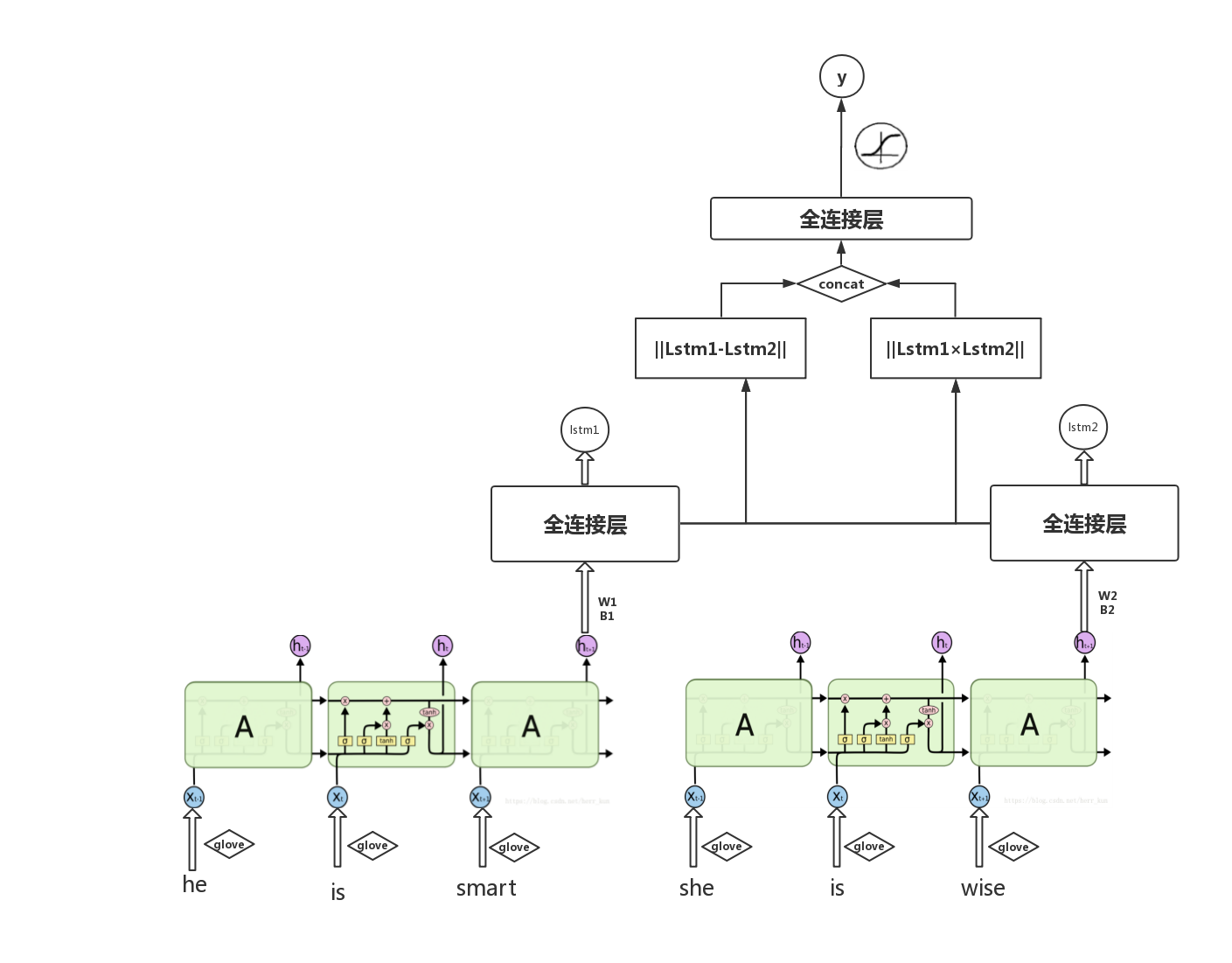
我尝试了单层的全连接层网络,对于单层的全连接网络我设置了不同的隐藏层节点,在初始学习率相同都为 1 的情况下,运行 3000 次迭代,实验效果如下图所示:
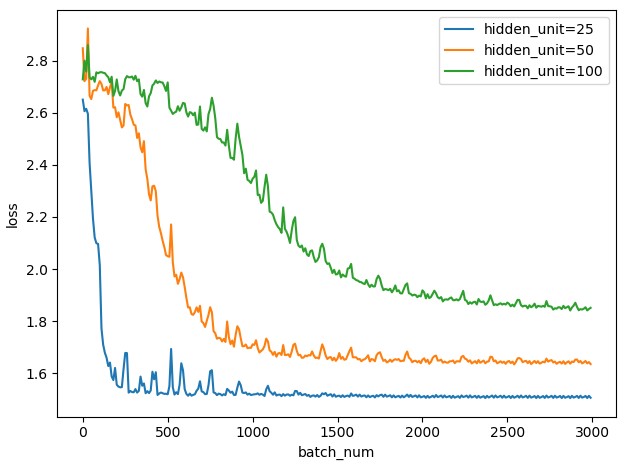
可以看到,隐藏层节点变化对模型的收敛速度和 终收敛的结果都有很大的影响。当节点数较多为 100 个的时候,模型的收敛速度比较慢,且在 1.9 左右时收敛速度就非常缓慢了。而对于 50 个节点的情况,模型初始收敛比 100 更快,可以理解时参数比较少导致的,而模型在 1.7 左右也进入收敛缓慢的状态。在 优,也就是 25 个节点的情况时,模型一开始就会有一个非常剧烈的下降过程,因为下降的太快,导致学习率一下就偏大了,于是出现了在 优点两侧的剧烈的波动,后面随着学习率指数递减,慢慢也逐渐可以收敛了。
可以看到用全连接层的方法也可以取得不错的效果,因此我考虑再在前面再添加一层全连接层,我们固定当前层的为 优情况 25 个隐藏节点,然后分别定义上一层的节点数为 32,64 和 128 再重复刚才的实验,在迭代 1500 次后可以看到实验效果如下:
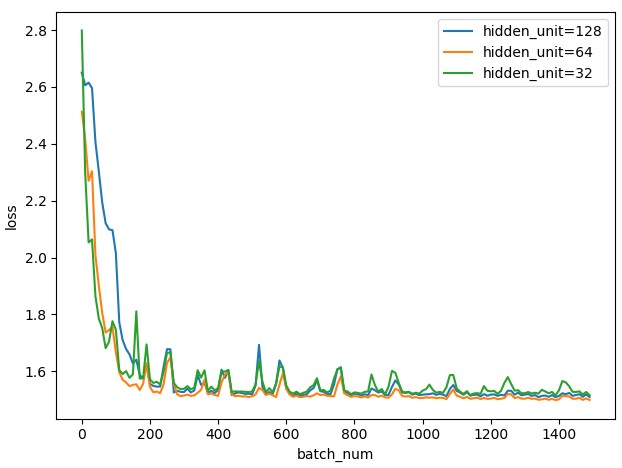
可以看到收敛的结果几乎相同,并不明显,当前一层的隐藏层节点数为 64 的时候,可以达到跟余弦相似度类似的实验效果,MSE 能收敛到 1.48 左右。因此可见增加更多的层或者节点数无限制的增加,效果不一定会更好。
组员分工
严宏昌 负责卷积神经网络部分 17341190 叶盛源 负责循环神经网络部分
参考文献
c++
[Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks][ https://arxiv.org/abs/1503.00075 ]
[Siamese Recurrent Architectures for Learning Sentence Similarity][ https://www.aaai.org/ocs/index.php/AAAI/AAAI16/paper/view/12195/12023 ]
[LSTM Neural Networks for Language Modeling][ https://www.iscaspeech.org/archive/interspeech_2012/i12_0194.html ]
Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[J]. arXiv preprint arXiv:1502.03167, 2015.
Keskar N S, Socher R. Improving generalization performance by switching from adam to sgd[J]. arXiv preprint arXiv:1712.07628, 2017.
Wilson A C, Roelofs R, Stern M, et al. The marginal value of adaptive gradient methods in machine learning[C]//Advances in Neural Information
He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.
Balduzzi D, Frean M, Leary L, et al. The shattered gradients problem: If resnets are the answer, then what is the question?[C]//Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017: 342-350.
Sandler M, Howard A, Zhu M, et al. Mobilenetv2: Inverted residuals and linear bottlenecks[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 4510-4520.
Lin T Y, Dollár P, Girshick R, et al. Feature pyramid networks for object detection[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 2117-2125.
参考文献
- 视频处理平台的设计与实现(北京交通大学·时月月)
- 基于用户画像的微博信息推荐模型研究(黑龙江大学·张冰)
- 物流设施选址系统的设计和实现(北京交通大学·黎宇彬)
- 基于机器学习的股票预测及股票推荐系统的设计与实现(北京交通大学·胡杰)
- 基于多类特征的股票走势预测及推荐系统(哈尔滨工业大学·魏侨池)
- 基于J2EE的地区电子政务系统的设计与实现(电子科技大学·薛刚)
- 基于混合策略的新闻推荐系统设计与实现(北京交通大学·郑宝瑞)
- 基于用户浏览模式的新闻推荐系统设计(云南财经大学·赵子慧)
- 基于SSH架构的个人空间交友网站的设计与实现(北京邮电大学·隋昕航)
- 基于Hadoop平台的个性化新闻推荐系统的设计与实现(北京交通大学·杨凯)
- 基于机器学习的股票预测及股票推荐系统的设计与实现(北京交通大学·胡杰)
- 金融信息实时发布系统的设计与实现(东北大学·伦健)
- 基于深度学习的新闻事件分析系统的研究与实现(北京邮电大学·俞书琪)
- 基于多模态融合的虚假新闻检测研究(中南财经政法大学·马银雪)
- 分布式智能网络爬虫的设计与实现(中国科学院大学(工程管理与信息技术学院)·何国正)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:源码客栈 ,原文地址:https://m.bishedaima.com/yuanma/36021.html