内容敏感的图像缩放
一、代码整体框架
bezier.hpp 提供了旋转 Bézier 曲面的相关功能,包括求曲线上的点、一阶导数、二阶导数的功能;
bezier_test.py 自己写的一个可视化 Bézier 曲线的脚本,方便调试;
kdtree.hpp 使用 PPM/SPPM 算法的时候存储碰撞点所用,支持统一更新碰撞点半径,在对数时间内查询碰撞点;
main.cpp 主程序接口,包含相机参数和初始化、景深效果、超采样等功能;
obj.hpp 定义了一些物体,有球、长方体、无穷大平面、旋转 Bézier 曲面;
ray.hpp 光线类,包含起点和方向;
render.hpp 渲染引擎,包含 PT、PPM、SPPM 等方法;
scene.hpp 渲染场景的定义;
texture.hpp 纹理类,每个 Object 都包含着一个 Texture,在 Texture 中可以存储图片、材质信息;
utils.hpp 最基本的一些定义;
vec3.hpp 三维向量的定义与运算,包括但不限于:四则运算、点积叉积、反射折射;
其中图片的读入采用 GitHub 上的开源仓库"stb"实现,图片的输出使用 ppm 格式,可直接以二进制方式写出。考虑到 ppm 格式的图像比较占内存,因此使用 Python 的 OpenCV 包将其转换为 png 格式。代码中除了使用 stb 读取图片之外, 其他全部的代码均为独立实现,共计代码 1184 行。
二、Bézier 曲线造型与曲面建模
2.1 Bézier 曲线造型
相关代码位于 bezier.hpp 中。
高次 Bézier 参数曲线由 n 个控制点构成, 参数 t ∈ [0,1]。Bézier 曲线需要解决两个问题:1. 求参数 t 对应点的坐标;2. 求参数 t 对应点的导数。
我并没有使用烂大街的 de Casteljau's[1] 算法,因为该算法对于 n 个控制点的
Bézier 曲线而言,每次需要花费 O(n2) 的时间计算,对于高次 Bézier 曲线并不友好,并且在作业中对于数值稳定性的要求不是很高。因此,我自己推导了一个只需要 O(n2) 预处理,之后的计算只需要 O(n) 的算法。
首先,由于 Bézier 曲线的 x,y 坐标是独立的,因此可以将该问题形式化为如下形式:
Theorem 1 给定 n + 1 个数值,分别将其记为 f0,f1,··· ,fn,令函数
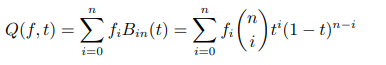
则 Q(x,t) 与 Q(y,t) 构成该 n 阶 Bézier 曲线。
Proof 1 根据定义,十分显然。
可以看出,函数 Q(f,t) 可以等价于一个关于 t 的 n 次多项式,不妨记为 Q(f,t) =
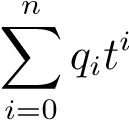
,如果能在多项式时间内求出 Q(f,t) 的系数,则可以在 O(n) 的时间内求出给定的 Bézier 曲线上的点,并且一阶导数、二阶导数也能够在 O(n) 的时间内计算得到。
Theorem 2 q0,q1,··· ,qn 可以在 O(n2) 的时间内求出。
Proof 2 详见参考文献 [6]。
2.2 Bézier 曲面建模
Bézier 曲面有两种建模方法:1. 用矩阵控制点描述曲面;2. 用曲线绕轴旋转构成曲面。代码中实现的是 Bézier 旋转体曲面,位于 obj.hpp 中。
我也没有使用烂大街的三维矩阵牛顿迭代求射线与 Bézier 曲面交点坐标,而是把该问题规约到了一个一元函数求零点的问题上。
Theorem 3 设 Bézier 曲面由 n 阶 Bézier 曲线 x(t),y(t) 绕旋转轴 y = y0 旋转而来,在三维空间中的形式为 (x(t)cosθ,y(t),x(t)sinθ),其中 θ 为曲线的旋转角度。则某条射线与该 Bézier 曲面有交点,当且仅当存在某个 y = yi 的平面上,射线与平面的交点到旋转轴的距离 dr,等于 Bézier 曲面与该平面的交点到旋转轴的距离 db。
Proof 3 显然。
如果我们枚举这个 y = yi 的平面,那么 dr 和 db 都是常数,因此可以认为 dr,db 是关于 y 的一个一元函数,该函数图像如图 1 所示。

图 1: 将 dr(y) 和 db(y) 的函数图像可视化,横坐标为 y,纵坐标中浅色的为 dr,深色的为 db
因此只要解方程 dr = db 即可得出旋转 Bézier 曲面与射线的交点的 y 坐标,进而求出交点。由高中的数学知识,经过一番简单的推导,可以得出方程 dr = db 等价于
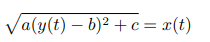
其中参数 a,b,c 与该射线相关,可经过计算得到;x(t),y(t) 为最初的 Bézier 曲线。该方程适用于任何形状的 Bézier 曲线。
由于 x(t),y(t) 可以看做一个关于 t 的一个 n 次多项式,因此该方程可以看做是一个次多项式求零点:g(t) = 0。理论上,多项式的所有零点都能通过一定的数值方法求得,但是出于效率的考虑,我直接对其采用牛顿迭代法求解。
我对 g(t) = 0 画过一些函数图像,发现它在 [0,1] 区间内比较平滑,在这个区间外是剧烈震荡,猜想是因为插值多项式的特性。采用原始的方程求解,一旦牛顿迭代中某一步的 x 到 [0,1] 之外,由于函数震荡,几乎不能收敛,这也解释了为什么三维情况比较难收敛的原因。此处使用的解决方案是,将 [0,1] 之外的函数值用一条直线抹平来代替原有的函数,这样如果有解,则一定会收敛到 [0,1] 内的某个解上。
该方法一个不足之处是,要对垂直于 y 轴射入的光线进行特判,对应到函数图像 1 上, dr 是一个斜率为无穷大的直线,方程相应变为
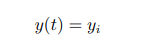
为一个 n 次多项式求零点的问题,求法同上,不再复述。
最终效果如图 2 所示。

图 2: 旋转 Bézier 曲线生成的花瓶
三、真实感场景渲染
3.1 光线与物体求交
代码位于 obj.hpp。
3.1.1 光线与无穷大平面求交
假设无穷大平面被表示为 ax + by + cz = 1,等价表示为 n···p = 1,射线为 o + td, o 为起点坐标,d 为方向向量,t > 0,因此交点方程为
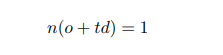 因此
因此
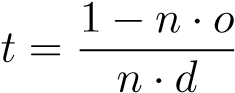
3.1.2 光线与球求交
球的方程可写为 (p c)2 = r2,带入射线方程即为 (o + td c)2 = r2,整理可得
 是一个关于 t 的一元二次方程,解之即可。
是一个关于 t 的一元二次方程,解之即可。
3.1.3 光线与长方体求交
射线与长方体的求交相当于射线对六个平面求交,在求交之后还需判定是否交点在长方形表面上。
3.1.4 光线与旋转 Bézier 曲面求交
在 2.2 小节已经叙述,此处不再重复。
3.2 反射、折射与 Fresnel 效应
代码位于 render.hpp
3.2.1 反射
反射光线计算公式为 R = I 2(I · N)N,其中 I 为入射光方向,N 为表面法向,R 为反射光方向。
3.2.2 折射
根据 Snell 定律,可以求得折射光的方向为
其中
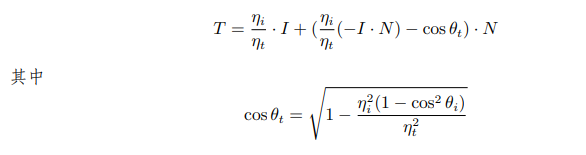
3.2.3 Fresnel 效应
当视线垂直于表面时,反射较弱,而当视线非垂直表面时,夹角越小,反射越明显。对于相同折射率为 η 的透明物体而言,由麦克斯韦电磁学方程推导出修正后的反射率和折射率:
其中
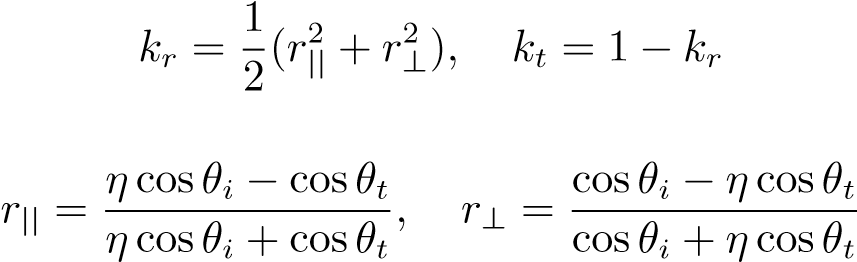
3.3 渲染算法
代码位于 render.hpp 中。
3.3.1 Path Tracing
Path Tracing[2] 是基本光线追踪的改良,有若干不同的版本,代码中简单实现了
Basic Path Tracing 的改良版本,在反射过程中统计直接光照。
Basic Path Tracing 在碰到漫反射面不终止,在半球上随机一个方向继续追踪,直到碰到光源。它可以采集到辉映效果,而焦散则难以采集(原因我觉得可能是对光源的追踪光路面积很小,随机打法难以打中),收敛极慢。
效果图如图 3 所示,渲染了好几天。

3.3.1 图 3: Path Tracing 效果图
3.3.2 Progressive Photon mapping
PPM[4] 大致流程如下:首先将光线跟踪中检测到的漫反射碰撞点组织成一颗 K-D Tree,K-D Tree 的实现方法参考 [5],代码位于 kdtree.hpp 中;然后从光源一轮轮均匀发射光子,对于落入碰撞点周围有效半径内的光子,估计其对于碰撞点的光亮度贡献,每一轮将碰撞点周围的有效半径减小一次。
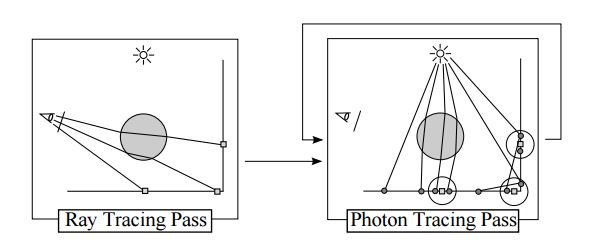
图 4: PPM 算法示意图
半径 R 的减小有 2 种方法:1. 全局固定半径 R 或不断缩小,查询碰撞点 R 范围近邻来统计光能;2. 根据论文公式
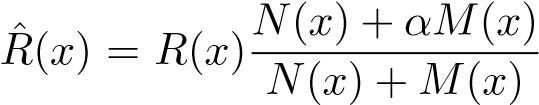
一轮轮修改每个碰撞点的半径。这两种方法各有好处,第一种方法计算快,对于细节收敛更快(非常锐利的焦散边缘),而第二种方法则全局暗部渲染较好,能保证无偏的完全收敛,但要产生锐利的焦散边缘则需要大量的光子。我两种方法都尝试了一下,最后选择了第一种方法。
效果图如图 5 所示,分辨率为 7680×4320,渲染了三天。更多结果可以查看 wallpaper 文件夹下的图片。

3.3.2 图 5: PPM 效果图
3.3.3 Stochastic Progressive Photon Mapping
SPPM[3] 相对于 PPM 增加了一个随机扰动,目的是超采样和抗锯齿。最终代码中即为
SPPM 的实现,从 PPM 直接改过来的,位于 render.hpp 和 main.cpp 中。
我跑了几张小图,发现也就是反射出来的星星更清晰了一些,其他基本没有差别,并且我在 PPM 实现的时候已经实现了抗锯齿的功能,效果差不多。考虑到渲染一张同样效果的大图所花的时间大于距离 DDL 的时间,因此就不放图了。
3.4 渲染特效
代码中实现了软阴影、超采样抗锯齿、纹理贴图和景深等功能,此处重点说明纹理贴图和景深的实现。
3.4.1 纹理贴图
对于某个物体而言,可以设定它的任意一点的颜色,可以从某张图中获取。比如图 5 中,地板的星星为一张基本的星星图片(第一次作业出来的图片)复制而成,左边的大球上的彩虹条纹为三维顶点经过一定的运算得出应该在图片的哪个像素点取颜色,这些变换函数具体位于 scene.hpp 中的 get_feature 函数中定义。
3.4.2 景深
光线追踪时,对每个像素点发出的射线,保持焦平面上的点不动,对射线发出处的端点做微小扰动,多次计算像素颜色后取平均值。在 main.cpp 中的 aperture 参数可以设置光圈半径,效果如图 6 所示。未加景深特效的渲染即为光圈半径为 0 时的情况。

图 6: 景深特效,可以看出相比图 5,玻璃球之后的部分更模糊
3.5 渲染加速
3.5.1 包围盒
在实现旋转 Bézier 曲面与光线求交的算法时,如果 dr 的最小值比 db 的最大值还要大,则说明该光线一定与曲面没有交点。相当于使用一个圆柱体包住旋转 Bézier 曲面。
3.5.2 K-D Tree
K-D Tree 主要用于 PPM/SPPM 算法找碰撞点,单次的查询复杂度在数据随机的情况下可看做 O(logn),其中 n 是 K-D Tree 中存储的点的个数。由于我没有实现网格/面片的相关功能(实现了还会扣分?),因此没有对 K-D Tree 进行更多的功能复用。
3.5.3 OpenMP
使用 C++ 中轻量级的多线程库 OpenMP 可将程序速度成倍提升。针对 PT 而言,可以将一张图一行行给一个线程运行;针对 PPM/SPPM 而言,可以将光源发射的光子数均分给若干个线程,每个线程出来一张缓存图片,等到所有线程都结束之后,再将其合并至一张图中,这样能够在不用加锁的情况下快速渲染。
四、图像降噪
我这一学期做了有关图像降噪的工作,训练了一个能够自动降噪的神经网络。出于某些原因,源代码和模型不能公开,但是效果图还是很好的,能够将渲染出来的图片去噪声去得几乎一颗噪点都不剩。
图 7(a)是计 42 班王赢绪同学的作品,直接从胡老师的 PPT 里面拿的,并且征得了王学长的同意;图 7(b)是降噪之后的效果。左右对比可以发现右图的质量明显优于左图,右图几乎没有一颗噪点。我还帮助了计 6 年级的某些同学进行图像降噪,如果有需要的话可以提供具体学生名
单和对应的图片。


原图 (b) 降噪之后的图
图 7: 图像降噪对比效果
参考文献
c++
De casteljau's algorithm. Accessed: 2018-06-30.
Kevin Beason. smallpt:
Global illumination in 99 lines of c++. Accessed: 2018-05-27.
Toshiya Hachisuka and Henrik Wann Jensen. Stochastic progressive photon mapping. ACM Transactions on Graphics (TOG), 28(5):141, 2009.
Toshiya Hachisuka, Shinji Ogaki, and Henrik Wann Jensen. Progressive photon mapping. In ACM Transactions on Graphics (TOG), volume 27, page 130. ACM, 2008.
Jiayi Weng. K-d tree 在信息学竞赛中的应用. . Published: 2016-7-31.
Jiayi Weng. 如何优雅地求和(清华集训 2016 解题报告). . Published: 2016-12-5.
参考文献
- 基于SSH架构的个人空间交友网站的设计与实现(北京邮电大学·隋昕航)
- 基于敏捷方法的软件研发项目管理系统的设计与实现(山东大学·孙凯)
- 基于SSH架构的个人空间交友网站的设计与实现(北京邮电大学·隋昕航)
- 基于J2EE的内容管理系统的设计与实现(南昌大学·舒婷)
- 印刷公司内容管理平台的设计与实现(吉林大学·郎彩虹)
- 复合规则驱动聚焦爬虫系统的设计与实现(哈尔滨工业大学·刘强)
- 基于MapGIS的地图服务系统的设计与实现(中国地质大学·汪鹏)
- 建筑设计院图档管理系统的设计与实现(吉林大学·时淮龙)
- 综合数据业务平台中内容管理系统的研究与设计(北京邮电大学·杨国梁)
- 适用于web需求的图片处理系统的设计与实现(北京工业大学·刘艳伟)
- 基于深度学习的图像美学推荐方法研究(北京工业大学·冯文颖)
- 基于SSH架构的个人空间交友网站的设计与实现(北京邮电大学·隋昕航)
- 高性能分布式图片服务器研究与实现(上海交通大学·王春)
- 基于WebGIS的快速解译制图系统的研究与实现(中国地质大学(北京)·周文豪)
- 基于SSH架构的个人空间交友网站的设计与实现(北京邮电大学·隋昕航)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:源码码头网 ,原文地址:https://m.bishedaima.com/yuanma/36039.html











