一、 理论知识
1.1 softmax线性分类器
线性分类器的函数为线性形式,即为(这里将偏置项看做参与乘积的一部分): $$ f(x_1,...x_m)=w_0+w_1x_1+...+w_mx_m=\bold x\bold w $$ 其中, $$ \bold x = [1,x_1,x_2,...,x_m]\ \bold w = [w_0,w_1,w_2,...,w_m]^T $$ 也就是找一组参数${w_k}^m_{k=1}$,使得在训练集上,函数与预测值尽可能接近。对于分类问题,线性回归的输出值与分类任务中的目标值不兼容。线性回归的结果范围为全体实数,而对于本次实验的多分类问题,变量结果即属于的类别,换言之,我们期望的结果标签的种类数量和训练样本的总类别数量一致。因此考虑使用softmax函数来将回归结果映射到种类上,从而表示分类结果。对于K分类问题,有: $$ softmax_i(\bold z)=\frac{e^{z_i}}{\sum^K_{k=1}e^{z_k}}\ f_i(\bold x)=softmax_i(\bold{xW})=\frac{e^{\bold{xw_i}}}{\sum^K_{k=1}e^{\bold{xw_k}}} $$ 其中,$\bold W$为: $$ \bold W\triangleq \left[\begin{matrix}{\bold w_1,\bold w_2...,\bold w_K}\end{matrix}\right] $$ 易见,所有类的softmax函数值之和为1。每一类的函数值就为它的概率。这就是softmax线性分类器。
1.2 多层感知机MLP
多层感知机由感知机推广而来,最主要的特点是有多个神经元层,因此也叫深度神经网络。相比单层的感知机,多层感知机引入了激活函数从而产生了非线性的变换,使得原本的分类超平面由线性变为了非线性,从而能够对线性不可分的数据进行更好的分类。多层感知机层与层之间是全连接的。多层感知机最底层是输入层,中间是隐藏层,最后是输出层。
对于每一层来说,输出的结果就是上一层的输入经过线性变换后再用激活函数处理的结果: $$ \bold x_n=f(\bold x_{n-1}\bold W_{n-1}) $$ 其中,$n$表示层数,$f( )$表示激活函数。输入层给出初始的$x_1$,与第一层的权重$\bold W_{1}$相乘,得到线性结果$\bold x_1\bold W_1$,再经过非线性的激活函数$f( )$处理得到$\bold x_2=f(\bold x_1\bold W_1)$,接着,将得到的$x_2$与隐藏层第二层的权重$w_2$相乘后经激活函数处理得到$x_3$......依次类推,经过多层处理,最终就能得到预测结果$\hat y$。
通过特定的损失函数度量预测结果$\hat y$与实际标签$y$的差距,将损失函数对每一层的所有参数进行求导从而得到梯度,使用梯度下降的方法训练各个参数。其中,每一层的反向传播求导遵循链式法则。设损失函数为$E$,第$l-1$层中,第$j$个节点到$l$层的第$i$个节点的权重为$w_l^{(i,j)}$,则有: $$ \frac{\part E}{\part w_l^{(j,i)}}=\frac{\part E}{\part f}\frac{\part f}{\part w_l^{(j,i)}}=\frac{\part E}{\part f}\frac{\part f}{\part x_l^{(j)}}\frac{{\part x_l^{(j)}}}{\part w_l^{(j,i)}} $$ 也就是说,需要从输出层开始,反向一层层求导。每一层权重的导数值为损失函数对激活函数求导后,再乘上用激活函数对权重参数求导的结果。这个结果可以看做是某一层的输出,再往前求导时同理,乘以对激活函数求导的值,再乘以激活函数对权重参数的导数值,一层层回推即可。
得到了每个参数的导数值后,就能通过梯度更新方法调整参数,减小损失: $$ \bold W_l=\bold W_l-\eta\frac{\part E}{\part \bold W_l} $$ 其中$\eta$为学习率。
通过多次的正向传播求结果和反向传播进行参数更新,使用得到的参数预测就能越来越接近想要的结果。
1.3 卷积神经网络CNN
卷积神经网络是多层感知机的变种。在上述的多层感知机中,每一层的输入节点到输出节点都有一个权重参数。如此一来,在规模较大、深度较深的网络中,会需要巨量的参数,从而使得训练和预测产生极大的开销。而卷积神经网络通过局部连接和权值共享,大大减少了参数数量。减少了权值的数量使得网络易于优化的同时,也降低了模型的复杂度,从而减小了过拟合的风险。
这些优点在网络的输入是图像时体现得更为明显,使得图像可以直接作为网络的输入,避免了传统识别算法中复杂的特征提取和数据重建的过程,在二维图像的处理过程中有很大的优势,如网络能够自行抽取图像的特征包括颜色、纹理、形状及图像的拓扑结构,在处理二维图像的问题上,特别是识别位移、缩放及其他形式扭曲不变性的应用上具有良好的鲁棒性和运算效率等。
卷积神经网络的基本结构包括:卷积层,池化层,全链接层。其中,全连接层的操作与上述的多次感知机一致。
卷积层是卷积神经网络的核心所在,其实质是空间滤波。以图像为例的话,卷积过程就是卷积核所有权重与其在输入图像上对应元素亮度之和。卷积之后,通常也会加入偏置, 并引入非线性激活函数: $$ conv_{x,y}=\sum^{p q}_iw_ix_i $$ 其中$(x,y)$为输入矩阵的空间坐标,$p q$为卷积核大小。
而池化层进行降采样操作,目的是降低特征图的特征空间。其操作和卷积操作基本一致,而步长通常等同于卷积核大小。同时,池化操作可以是线性的,如平均池化,也可以非线性的,如最大池化和$L_2$池化等。
同样,像多层感知机一样,通过多次的正向传播求结果和反向传播进行参数更新,使用得到的参数预测就能越来越接近想要的结果。
二、 代码实现
本次实验我使用的深度学习框架是python的PyTorch。
2.1 数据的预处理
读入数据集时,训练集和验证集各含有50000和10000个样本。将样本拆分成输入特征
data
和标签
label
,将二者合并成列表存入
trainset
中。其中,输入的特征为图像,大小为32*32,有三个颜色通道。以训练集为例,读入部分的代码如下:
python
trainset = []
train_images = np.load("cifar10_train_images.npy")
train_labels = np.load("cifar10_train_labels.npy")
for i in range(50000):
data = torch.Tensor(train_images[i])
label = train_labels[i]
trainset.append([data, label])
最后,用PyTorch的DataLoader类保存全部的数据。这里可以调整
batch_size
参数,从而在之后的训练过程中实现mini size batch。我设置的参数为100,即每个batch的大小为100。
python
trainloader = torch.utils.data.DataLoader(trainset, batch_size=100, shuffle=False, num_workers=0)
2.2 训练过程
首先创建神经网络实例:
python
net = Net()
这里的
Net
类可以依据需要进行修改。按照本次实验要求,我实现了softmax线性分类器、多层感知机、卷积神经网络三种网络,其定义在下文会详细说明。
通过PyTorch给出的接口,可以直接定义损失函数和优化方法。除了之后特殊说明的地方,我使用的都是交叉熵损失和批梯度下降的方法。其定义如下:
python
criterion = nn.CrossEntropyLoss() # 损失函数
optimizer = optim.SGD(net.parameters(), lr=0.001) # 批梯度下降,学习率为0.001
定义好训练的参数后就可以进行训练了:
python
for epoch in range(10): # 学习次数
running_loss = 0.0 # 损失函数值,用于统计每次学习后的损失
for i, data in enumerate(trainloader, 0):
inputs, labels = data
optimizer.zero_grad() # 将参数梯度清零
outputs = net(inputs) # 前向传播
loss = criterion(outputs, labels) # 计算损失
loss.backward() # 反向传播
optimizer.step() # 更新梯度
每轮训练后,可以累加损失值并输出,观察训练对损失函数值的影响:
python
running_loss += loss.item() # 累加当前损失,用于计算样本平均损失值
if i % 10 == 9:
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
2.3 验证过程
验证集的读入与训练集的读入基本一致,不再进行赘述。
读入验证集后,将验证集的数据经分类器处理,得到结果,如果预测结果与实际标签一致则预测正确,否则预测失败。统计预测正确的个数和验证集样本的总个数,从而可以算出准确率:
```python correct = 0 # 正确个数 total = 0 # 总个数 with torch.no_grad(): for data in testloader: images, labels = data outputs = net(images) # 预测结果 _, predicted = torch.max(outputs.data, 1) total += labels.size(0) correct += (predicted == labels).sum().item() # 比较结果
print('Accuracy of the network on the 10000 test images: %d %%' % ( 100 * correct / total)) ```
2.4 神经网络的定义
为了统一使用上述的训练过程,对于本次实验的十分类问题,神经网络的输出都为10维的向量,并且最后都通过softmax处理,从而能够选择数值最大的那一个维度作为分类结果。
首先是softmax线性分类器。对于本次实验的十分类问题,通过输入大小为$3 32 32$的参数进行加权求和,最终得到10个结果,再将是个结果通过softmax处理,得到最终的结果:
```python class Net(nn.Module): def init (self): super(Net, self). init () self.fc = nn.Linear(3 * 32 * 32, 10) self.softmax = nn.Softmax()
def forward(self, x):
x = x.view(-1, 3 * 32 * 32) # 将3*32*32的矩阵转换为向量,从而将矩阵展平
x = self.softmax(self.fc(x))
return x
```
我实现的MLP更加复杂一些,需要通过三个隐藏层,每一层的激活函数都为ReLU函数。最终,输出层通过softmax处理。除了最后实验结果分析时改动了层数和神经元参数会进行特别说明外,其他部分的实现代码都如下:
```python class Net2(nn.Module): def init (self): super(Net2, self). init () self.fc1 = nn.Linear(3 * 32 * 32, 1000) self.fc2 = nn.Linear(1000, 500) self.fc3 = nn.Linear(500, 100) self.fc4 = nn.Linear(100, 10) self.softmax = nn.Softmax() self.relu = nn.ReLU()
def forward(self, x):
x = x.view(-1, 3 * 32 * 32)
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.relu(self.fc3(x))
x = self.softmax(self.fc4(x))
return x
```
卷积神经网络则是依次通过卷积层、池化层、卷积层、池化层,再通过三个全连接层。卷积神经网络的各层的参数是依据LeNet-5设置的。除了LeNet-5的输入为单通道,而本次实验的输入图像有RGB三个通道外,其他的参数都相同。实现代码如下:
```python class Net3(nn.Module): def init (self): super(Net3, self). init () self.conv1 = nn.Conv2d(3, 6, 5) self.pool = nn.MaxPool2d(2, 2) self.conv2 = nn.Conv2d(6, 16, 5) self.fc1 = nn.Linear(16 * 5 * 5, 120) self.fc2 = nn.Linear(120, 84) self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
```
三、实验结果与分析
3.1 三种模型的对比
使用上面代码实现部分所用的参数进行实验,最终得到的准确率为:
| 线性分类器 | 多层感知机 | 卷积神经网络 |
|---|---|---|
| 10% | 70% | 67% |
线性分类器的分类结果最差,这是因为图片对象具有高度的线性不可分性。单纯的进行单层的线性变化难以将多达十种类别的图片进行划分。这个实验很好地暴露了线性分类器的缺点:面对线性不可分的实际问题,线性分类器的效果奇差。实际上,在训练过程中,线性分类器的损失函数一开始就几乎收敛了(下图方括号中的第一个数字表示训练次数,第二个数字表示已经训练了几个mini batch):

数次训练后,其损失函数也几乎没什么变化:
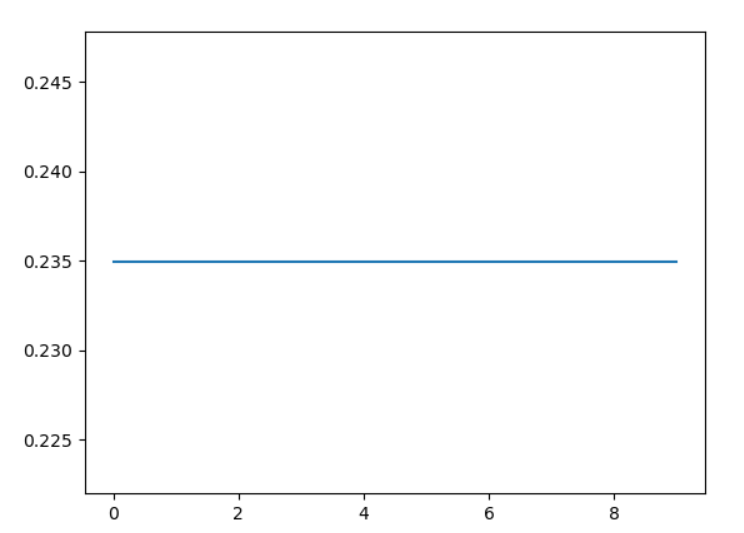
上图的横轴为1~10,表示训练的除数,纵轴表示损失函数值。因为我采用的是mini batch size的方法,故使用每次训练时的最后一个batch的损失函数均值作为整体的损失函数值。
相对线性分类器来说,多层感知机具有更好的表现。其损失函数变化图像如下:
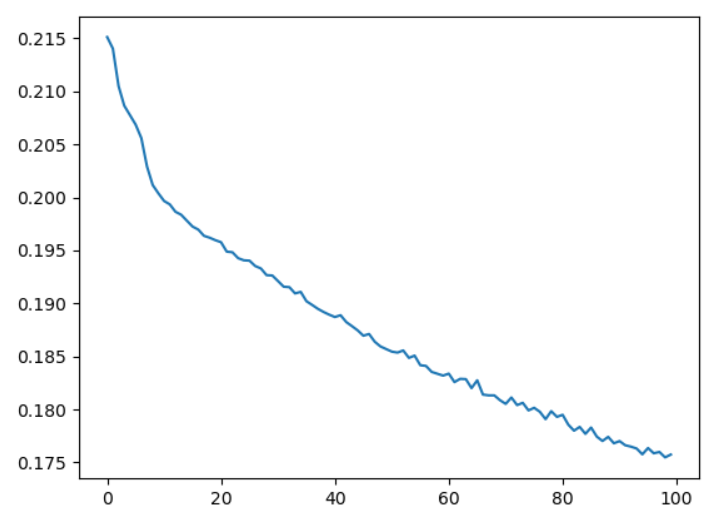
可以看出,经过100次的训练,多层感知机仍然并未完全收敛,通过改进网络结构、修改超参数、增多训练次数等方法,可以进一步提高最后的准确率。而对于10分类问题来说,70%的准确率已经较优了。可以看出,在多层感知机引入非线性函数和多层的概念后,分类效果相较单纯的线性分类器极大的提升了。
使用卷积神经网络得到的损失函数变化如下图所示:
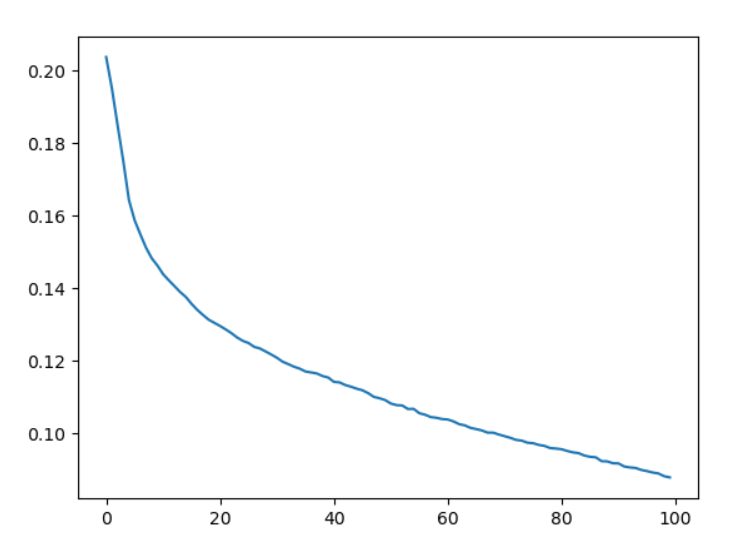
可以看到,相较多层感知机,使用卷积神经网络有更快的收敛速度,最终得到的损失也更小。
经上面的实验不难看出,相比于线性softmax分类器来说,具有非线性成分的多层感知机和卷积神经网络效果明显更优。对于线性不可分的数据,引入的非线性成分极大地提高了模型性能。
3.2 网络层数和神经元数量对MLP的影响
在上面的实验中,我的MLP具有3个隐藏层和一个输出层,其中三个隐藏层的节点数分别为$3\times3\times32$、$1000$、$500$、$100$,输出层的节点数为$10$;隐藏层的激活函数都为ReLu函数,输出层为softmax函数。
现在将上面的模型称为MLP1,并对其进行改造,减少网络层数。首先去掉神经元个数为1000的层,将修改后的模型称为MLP2。在MLP2的基础上,去掉节点数为500的模型,称为MLP3。在MLP3的基础上,去掉神经元个数为100的层,称为MLP4。
在同样的学习率(0.001)和训练次数(100次)下,四个不同的MLP模型训练后的准确率为:
| MLP1(4层) | MLP2(3层) | MLP3(2层) | MLP4(1层) |
|---|---|---|---|
| 70% | 61 % | 42% | 10% |
再在MLP1的基础上,重新改造形成新模型。这次试着减少神经元数量。首先将MLP1的隐藏层的每一层的节点数减半,新模型称为MLP2。MLP1隐藏层的节点数变为原来的1/5,作为MLP3。节点数变为原来的1/10,作为MLP4。
在网络结构基本相同,只是隐藏层节点数不同的情况下重复试验,得到了如下结果:
| MLP1 | MLP2(节点数减半) | MLP3(节点数变为1/5) | MLP4(节点数变为1/10) |
|---|---|---|---|
| 70% | 52% | 49% | 40% |
从上面的结果不难看出,MLP模型的层数越多(或者说网络越深)、节点数越多,预测的结果就越准确,也就是模型的性能越好。这是因为通过增加神经网络的深度和网络中的节点数,整个模型的复杂度上升了。复杂的模型对数据具有更好的拟合能力,因此最终呈现出了更佳的模型性能。对复杂的网络进行足够充分的学习后,能更好的拟合数据。当然,也存在过拟合的风险。
3.3 不同模型结构因素对CNN的影响
以LeNet-5模型为基础,对部分结构进行部分改变,其他结构相同,在学习率为0.01、训练次数为10次(卷积神经网络训练速度较慢,所以我增加了学习率并减少了迭代次数)的情况下,可以得到如下的准确率结果:
| 原模型 | 去掉第一个卷积层 | 去掉第二个卷积层 | 去掉两个卷积层 |
|---|---|---|---|
| 52% | 10% | 10% | 10% |
| 原模型 | 滤波器数量变为原来的1.5倍 | 滤波器数量减半 |
|---|---|---|
| 52% | 68% | 46% |
| 原模型 | 去掉第一个池化层 | 去掉第二个池化层 |
|---|---|---|
| 52% | 81% | 63% |
得到的结论和上面基本一致。CNN增加卷积层、增加滤波器数量、减少池化层能够增加模型的复杂度,从而使得模型更好地拟合数据,以此达到更好的性能。理论上,更加复杂的模型经过足够的学习训练后,可以有更优的性能,但模型过于复杂可能导致过拟合,导致在测试样本上效果不佳,同时也会增加训练和预测的时间开销,因此,模型复杂度也不是越高越好。
3.4 不同算法的影响
使用python的
time
模块可以对训练时间进行统计。分别使⽤ SGD 算法、 SGD Momentum 算法和 Adam 算法训练模型,SGD算法的学习率为0.001,Adam为0.000001;学习次数都为10,以原来的MLP模型为例,可以得到以下的准确率结果:
| 算法 | SGD算法 | SGD Momentum算法(momentum=0.9) | Adam算法(betas=(0.9,0.99)) |
|---|---|---|---|
| 准确率 | 42% | 42% | 35% |
| 训练用时(秒) | 250.1 | 275.1 | 499.3 |
三个算法的损失函数变化分别如下:



虽然SGD需要走很多步的样子,但是对梯度的要求很低(计算梯度快),但SGD在随机选择梯度的同时会引入噪声,使得权值更新的方向不一定正确。此外,SGD也没能单独克服局部最优解的问题。动量Momentum主要解决SGD的两个问题:一是随机梯度的方法(引入的噪声);二是SGD在收敛过程中和正确梯度相比来回摆动比较大的问题。 Adam中动量直接并入了梯度一阶矩(指数加权)的估计,并包括偏置修正,修正从原点初始化的一阶矩(动量项)和(非中心的)二阶矩估计。Adam算法既可以减缓波动,又使得学习步子变大,从而达到加快学习的目的。
参考文献
- Semi-supervised Node Classification Based on Graph Markov Convolution Neural Network(华中师范大学·Yuanming Gu)
- 基于颜色特征的图像检索系统设计与实现(沈阳工业大学·邸洪波)
- 基于用户画像的推荐系统的设计与实现(东北大学·鲁墨)
- 基于知识图谱的图像描述改进(云南大学·王雁鹏)
- 基于深度学习的商品图片检测算法(河北经贸大学·赵子露)
- 融合知识图谱和多模态的文本分类研究(河南财经政法大学·姚克)
- 基于知识图谱的图像描述改进(云南大学·王雁鹏)
- 基于深度学习的定制化图像识别系统的设计与实现(贵州大学·姜建勇)
- 基于视频分享社交系统后台的设计与研发(中国地质大学(北京)·刘昌瑞)
- Semi-supervised Node Classification Based on Graph Markov Convolution Neural Network(华中师范大学·Yuanming Gu)
- 基于SSH框架的图像检索系统的设计与实现(内蒙古大学·高凌超)
- 基于人脸聚类的图片管理系统的设计与实现(首都经济贸易大学·王子涛)
- 基于元学习的少样本图像识别方法研究(中国矿业大学·储蓄)
- 基于影像特征的艺术品识别检索系统设计与开发(东南大学·张雨露)
- 基于用户画像的知识付费产品推荐研究(黑龙江大学·刘子瑞)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:源码导航 ,原文地址:https://m.bishedaima.com/yuanma/36053.html











