Python 数据分析

实验目的及实验内容

（本次实验所涉及并要求掌握的知识；实验内容；必要的原理分析）

实验目的：

使用 python 进行图像处理

实验内容：

自己找一张图片，用 OpenCV 的仿射变换实现图片缩放。

理解 HOG、ORC 过程，修改 digits.py 或独立编程，实现数字图像的识别，要求分别使用 SVM、knn（第六次课）以及 cnn 神经网络模型（第七次课），以群文件中 digit_data.rar 中 train 文件夹下数据作为训练集，test 文件夹下图片作为测试集，并计算测试集上分类正确率，并自己找测试数据（可以是一个或多个数字）。

原理分析：

用 OpenCV 的仿射变换实现图片缩放：先说仿射变换：

一个任意的仿射变换都能表示为乘以一个矩阵（线性变换）接着再加上一个向量（平移），即旋转相当于线性变换、平移相当于向量加、缩放操作相当于线性变换等。

我们通常使用 2 x 3 矩阵来表示仿射变换，其中左边的 2×2 子矩阵是线性变换矩阵，右边的 2×1 的两项是平移项：

对于图像上的任一位置（x, y），仿射变换执行的是如下的操作：

需要注意的是，对于图像而言，宽度方向是 x，高度方向是 y，坐标的顺序和图像像素对应下标一致，因此原点的位置是左上角而不是左下角，y 的方向是向下而不是向上。

当对一张图像执行缩放操作时，实际上只执行线性变换而不执行平移，因此矩阵 A 和矩阵 B 的构造应如下所示：

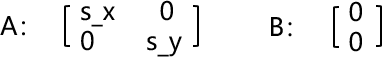
其中 s_x、s_y 分别表示 x 坐标和 y 坐标的缩放比例，对于缩小操作而言，s_x、s_y 的取值范围为(0, 1]。

导入 openCV 时，实际上应该导入 cv2。该包有一个函数 cv2.warpAffine(src, M, dsize, dst,flags, borderMode, borderValue)可以实现仿射变换，其各参数说明如下： InputArray src：输入的图像；

InputArray M：透视变换的矩阵，即 A 和 B 的拼接； Size dsize：输出图像的大小，宽高应为整数； OutputArray dst：输出的图像；

flags=INTER_LINEAR：输出图像的插值方法，如 cv.INTER_NEAREST 向邻近元素借值、cv.INTER_LINEAR 使用附近四个点的颜色值进行双线性插值等（默认为后者）。borderMode=BORDER_CONSTANT：图像边界的处理方式； borderValue=Scalar()：边界的颜色设置，一般默认是 0（黑色）。

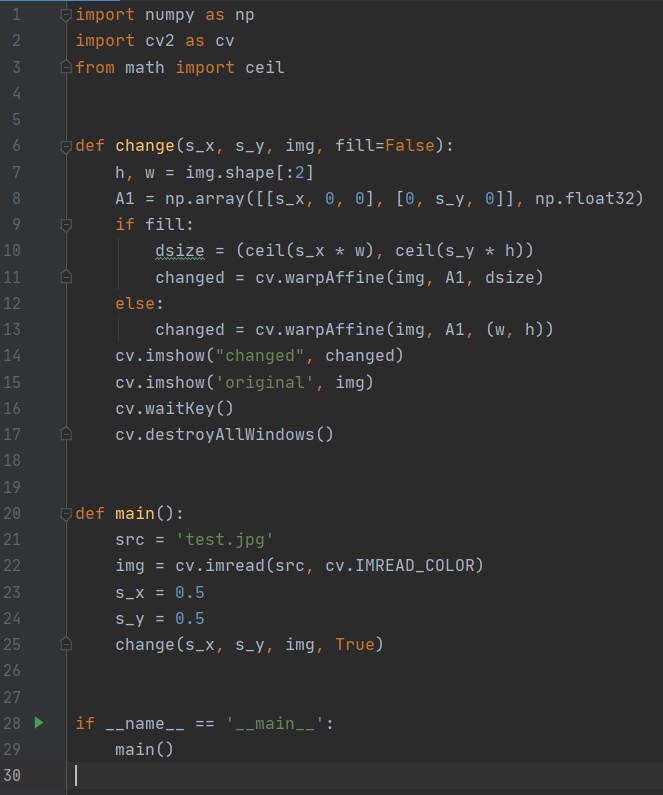
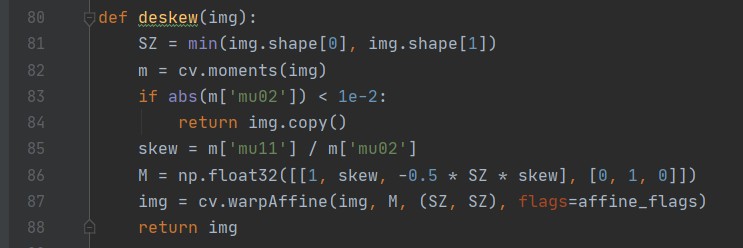
确定好矩阵 M 后直接调用 cv2.warpAffine()函数，然后打印送显即可。相关代码如下图所示：

其中 fill 作为标志位用于确定用户是否想要将窗口适应为图像大小。使用 SVM 进行数字图像识别：

使用 SVM 和 KNN 在进行分类时都需要预先提取图像特征。方向梯度直方图（Histogram of Oriented Gradient, HOG）特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子，它通过计算和统计图像局部区域的梯度方向直方图来构成特征。

HOG 特征提取方法就是将一个 image 依次做如下操作：

灰度化（将图像看做一个 x，y，z（灰度）的三维图像；

采用 Gamma 校正法对输入图像进行颜色空间的标准化（归一化）；目的是调节图像的对比度，降低图像局部的阴影和光照变化所造成的影响，同时可以抑制噪音的干扰；

计算图像每个像素的梯度（包括大小和方向）；主要是为了捕获轮廓信息，同时进一步弱化光照的干扰。

将图像划分成小 cells（本实验中采用的是 10*10 像素/cell）；

统计每个 cell 的梯度直方图（不同梯度的个数），即可形成每个 cell 的 descriptor； 6）将每几个 cell 组成一个 block（例如 2*2 个 cell/block），一个 block 内所有 cell 的特征

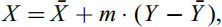
校正效果如下图所示，图左为原图，图右为校正后的图片：

在该部分实验中，分类器采用的是 SVM，其相关介绍如下所述：

SVM 是支持向量机，它会将样本的两种特征用一条直线或者超平面分开，并且保证间隔最大。

SVM 的基本思想可以概括为：首先通过非线性变换将输入空间变换到一个高维空间，然后在这个新空间中求取最优线性分类面，而这种非线性变换是通过定义适当的内积函数（核函数）实现的。

SVM 求得的分类函数形式上类似于一个神经网络，其输出的若干中间层节点的线性组合，而每一个中间层节点对应于输入样本与一个支持向量机的内积，因此也被称为支持向量网络。由于最终判决函数中实际只包含与支持向量的内积和求和，因此识别时的计算复杂度取决于支持向量的个数。

SVM 效果好坏的重要决定因素之一是核函数的选择，一般可供选择的核函数有线性核、多项式核、高斯（RBF）核函数、sigmoid 核函数。在选择核函数时一般考虑以下几点：

如果特征的数量大到和样本数量差不多，则选用 LR 或者线性核的 SVM；

如果特征的数量小，样本的数量正常，则选用 SVM+ 高斯核函数；

如果特征的数量小，而样本的数量很大，则需要手工添加一些特征从而变成第一种情况。

本实验中采用的是高斯核函数。

除了核函数的选取，SVM 的策略对 SVM 的性能也十分重要。手写数字字体识别显然是个多类别分类问题，对于多分类问题，解决的基本思路是“拆分法”，即将多个二分类问题拆分为若干个十分类任务进行求解。具体来讲，先对问题进行拆分，然后为拆出的每个十分类任务训练一个分类器，在测试时，对这些二分类器的结果进行集成以获得最终的多分类结果。拆分的策略主要有以下几种：

OvO（one-vs-one）

这种解决方法的思路是：对于有 N 个类别的分类任任务，将这 N 个类别两两配对，从而产生 N(N-1)/2 个二分类任务。在测试阶段，新样本同时提交给所有分类器，这样可以得到 N(N-1)/2 个分类结果，最终的结果可以通过投票产生：即把预测的最多的类别作为最终的分类结果。

OvR（one-vs-rest）

这种解决方法的思路是：每次将一个类的样例作为正例，所有其他类的样例作为负例来训练 N 个分类器。在测试时，若仅有一个分类器预测为正类，则对应的类别标记为最终分类结果。

本实验采用的是 OvR 策略。

采用的是 sklearn 库的 SVM 分类器，相关代码如下所示：

至此，使用 HOG + SVM 的手写数字图像识别的流程为：

图像文件输入 → 图像校正 → 图像特征（HOG）提取 → 划分好训练集和测试集 → 训练集送 SVM 分类器训练 → 测试集送已训练好的分类器预测 → 计算正确率 → 送自检数据到 SVM 分类器预测 → 识别结果输出

使用 KNN 进行手写数字图像识别：

使用 KNN 做手写数字图像识别的任务的预处理流程和 HOG+SVM 差不多，只是分类器的选择从 SVM 变成了 KNN。KNN 的相关介绍如下所述：

KNN 是通过测量不同特征值之间的距离进行分类。它的思路是：如果一个样本在特征空间中的 k 个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中 K 通常是不大于 20 的整数。KNN 算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

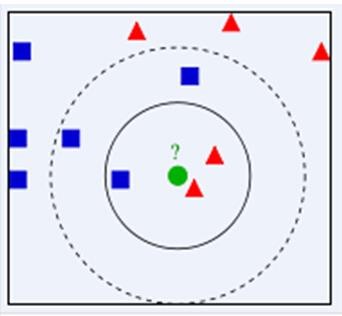
下面通过一个简单的例子说明一下：如下图，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果 K=3，由于红色三角形所占比例为 2/3，绿色圆将被赋予红色三角形那个类，如果 K=5，由于蓝色四方形比例为 3/5，因此绿色圆被赋予蓝色四方形类。

由此也说明了 KNN 算法的结果很大程度取决于 k 的选择。

在 KNN 中，通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离；同时，KNN 通过依据 k 个对象中占优的类别进行决策，而不是单一的对象类别决策。这两点就是 KNN 算法的优势。

算法的描述为：

计算测试数据与各个训练数据之间的距离；

按照距离的递增关系进行排序；

选取距离最小的 K 个点；

确定前 K 个点所在类别的出现频率；

返回前 K 个点中出现频率最高的类别作为测试数据的预测分类。

本实验中采用的是 sklearn 库的 KNN 做分类器，相关代码如下图所示：

使用 CNN 进行数字图像识别：

CNN 是卷积神经网络，属于深度学习的范畴。它的基础是神经网络，然而神经网络在做图像识别的时候需要大量的神经元并进行大量的计算，计算代价太大，因此考虑用卷积神经网络。

卷积的思想来源于特征提取，譬如我们看一张猫的图片，可能看到猫的眼睛或者嘴巴就知道这是一张猫的照片，而不必等看完整个照片的每一个像素点再做判断；所以如果我们可以用某种方式对一张图片的某个或某些典型特征做出识别，那么这张图片的类别也就知道了。这个时候就产生了卷积的概念：把大量的数据做特征提取，最后对提取到的特征做累计投票，将票选的结果作为分类结果。

卷积神经网络中有三个比较重要的“层”：卷积层（Convolution Layer）、池化层（Pooling Layer）、Flatten 层 & 全连接层（Fully Connected Layer）。

卷积层：

卷积层相当于是，用若干个卷积核“滑过”图像的每一块并对其做计算，得到一张新的图像。卷积核是一个矩阵，其大小由人为指定。就像是一个过滤器，过滤器通过每次移动一个单元的方式对输入内容进行卷积，过滤器移动的距离就是步幅。一般而言，如果不做填充的话，一次卷积过后图像的大小会减少，减少量与步幅有关。计算任意给定卷积层的输出的大小的公式是：

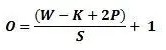
其中 O 是输出尺寸，W 是输入尺寸，K 是过滤器尺寸，P 是填充，S 是步幅。

在卷积层中每个神经元连接数据窗的权重是固定的，每个神经元只关注一个特性。神经元就是图像处理中的滤波器，比如边缘检测专用的 Sobel 滤波器，即卷积层的每个滤波器都会有自己所关注一个图像特征，比如垂直边缘，水平边缘，颜色，纹理等等，这些所有神经元加起来就好比就是整张图像的特征提取器集合。

把卷积层输出结果做非线性映射。CNN 采用的激活函数一般为 ReLU(The Rectified Linear Unit/修正线性单元)，它的特点是收敛快，求梯度简单，但较脆弱。

池化层：

池化层夹在连续的卷积层中间，用于压缩数据和参数的量，减小过拟合。简而言之，如果输入是图像的话，那么池化层的最主要作用就是压缩图像。

池化层的具体作用一般有三点：

保留特征。池化操作就是图像的 resize，比如我们将一张猫的照片由 56 56 缩小到 28 28 时仍能认出这是一张猫的照片，就是因为缩小的过程中，这张图像中仍保留着猫最重要的特征，我们一看就能判断图像中画的是一只猫。图像压缩时去掉的信息只是一些无关紧要的信息，而留下的信息则是具有尺度不变性的特征，是最能表达图像的特征。

特征降维。一幅图像含有的信息是很大的，特征也很多，但是有些信息对于我们做图像任务时没有太多用途或者有重复，我们可以把这类冗余信息去除、把最重要的特征抽取出来，这也是池化操作的另一重要作用。

在一定程度上防止过拟合，更方便优化。

池化层用的方法有 Max pooling 和 average pooling，而实际用的较多的是 Max pooling，本次实验中采用的也是 Max pooling。Max pooling 就是最大池化，其基本思想是将图像分为若干个块儿，每个块儿保留最大的数值作为该块儿的特征，然后再将处理后的特征拼到一起形成新的图像，新的图像可以认为是旧图像的特征集合。

全连接层：

两层之间所有神经元都有权重连接，通常全连接层在卷积神经网络尾部。全连接层一般会把卷积输出的二维特征图转化为一维的一个向量，全连接层的每一个节点都与上一层的每个节点连接，是把前一层的输出特征都综合起来，所以该层的权值参数是最多的。其作用就是将最后一层卷积得到的 feature map stretch 成向量，对这个向量做乘法，最终降低其维度，然后输入到 softmax 层中得到对应的每个类别的得分。

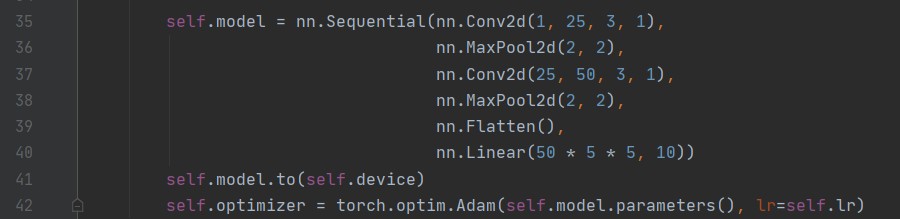
在本实验中，数据集为 28*28 的图像，通过 torch.tensor 转化成 torch.Size([n, 1, 28, 28])的 tensor，然后将（batch，1，28，28）大小的 tensor 输入模型 CNN。CNN 的构建如下图所示：

对这个网络的解释为：

第 1 层卷积层的卷积核为 3 3，步幅为 1，共 25 个。输入的 1 28 28 的数据经过该层卷积，得到 25 26*26 的输出；

第 2 层池化层采用最大池化，池化窗口的大小是 2 2。将第 1 层卷积后得到的 25 26 26的数据送入该层池化，得到 25 13*13 的输出；

第 3 层卷积层的卷积核为 3 3，步幅为 1，共 50 个。输入的 25 13 13 的数据经过该层卷积，得到 50 11*11 的输出；

第 4 层池化层采用最大池化，池化窗口的大小是 2 2。将第 3 层卷积后得到的 50 11 11的数据送入该层池化，得到 50 5*5 的输出；

将第 4 层池化后的 50 5 5 送入 flatten 层“拍平”后全连接，得到 1250 的结果；

将 1250 的结果送入 linear 层，通过线性分类器，分出 10 个标签对应的概率值。将这个网络送入若干个 epoch 训练，用交叉熵计算 loss，并用 Adam 做优化。

在用 CNN 做预测时，需要禁止梯度计算，随后将测试集数据送入 CNN，然后将 CNN 的输出中概率值最大的一项作为预测结果。

实验环境

（本次实验所使用的器件、仪器设备等的情况）

处理器：Intel(R) Core(TM) i5-9300H CPU @ 2.40GHz 2.40 GHz (2)操作系统环境：Windows 10 家庭中文版 x64 19042.867

编程语言：Python 3.8

其他环境：16 GB 运行内存

IDE 及包管理器：JetBrains PyCharm 2020.1 x64， anaconda 3 for Windows（conda 4.9.0）

实验步骤及实验过程分析

（详细记录实验过程中发生的故障和问题，进行故障分析，说明故障排除的过程及方法。根据具体实验，记录、整理相应的数据表格、绘制曲线、波形等）

说明：

本篇实验报告所记录的内容仅为写报告时（2021/05/12）的情况，可能与实际实验时/04/28）结果有出入。

一切以实际运行时所得到的结果为准。

用 OpenCV 的仿射变换实现图片缩放：

原图及缩放后的结果分别如下图左和下图右所示：

我在输出图片时顺便调整了窗口适应图片大小。如果不调整的话，原图及缩放后的结果分

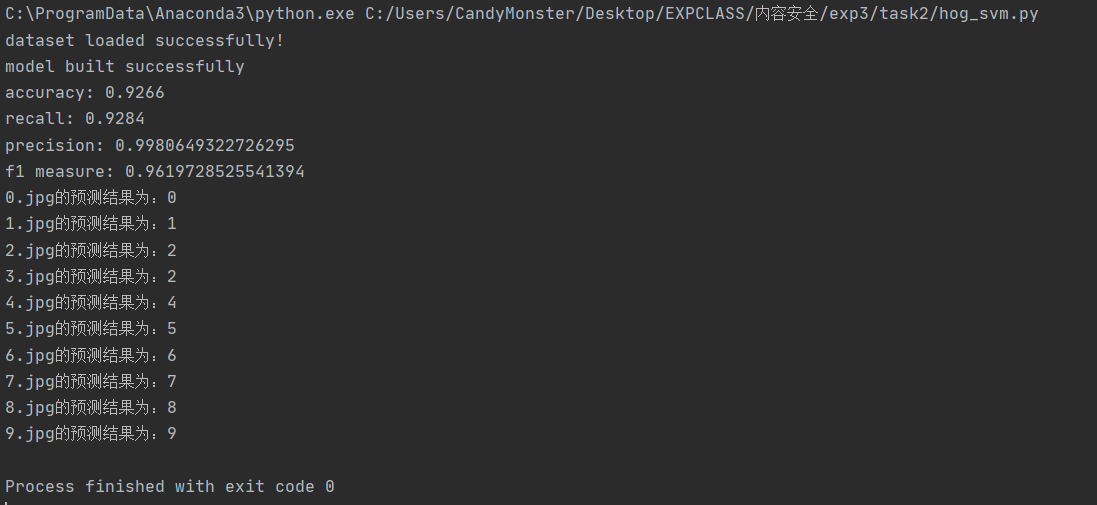
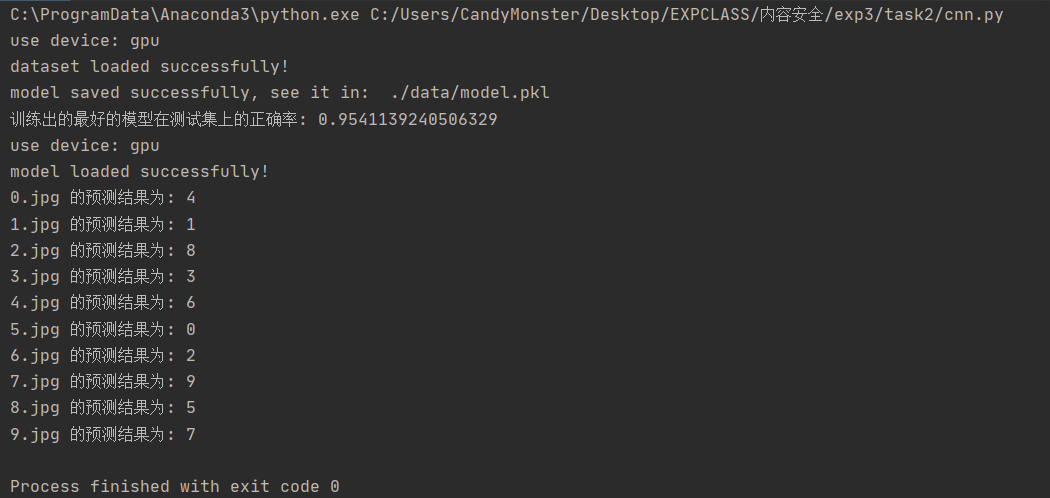
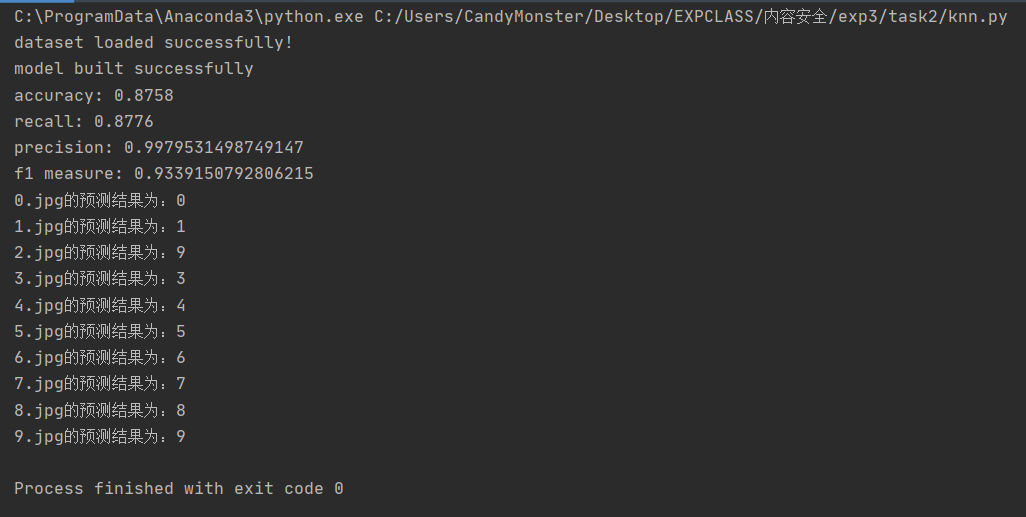
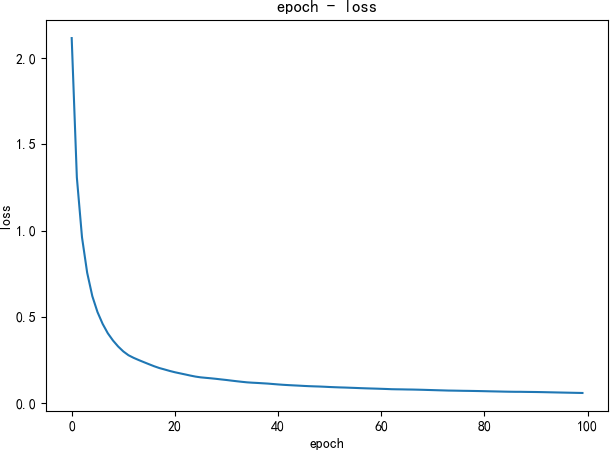
呃…在训练集和测试集上的效果是比较不错，但是在真正用于分类的时候，效果显然是有点逊的。

实验结果总结

（对实验结果进行分析，完成思考题目，总结实验的新的体会，并提出实验的改进意见）

本次手写数字图像识别实验理论理解起来有些困难，但实际操作起来很简单，使用前人已经造好的轮子就可以很方便地完成实验。然而重要的并不是实验结果，而是实验原理，因此通过实验明白实验原理对日后的发展有很大用处。

SVM 方面，有很多参数都会对实验结果产生较大的影响，如核函数的选择、策略的选择、核函数与策略的组合等。或许应当测试一下不同选择对准确率的影响。

KNN 的效果主要取决于 k 的选择，或许应当测试一下不同 k 对准确率的影响。

CNN 是我以前一直没弄明白的东西，神经网络这块我一直都不是很熟悉，只知道大概的流程如卷积、池化之类的，但具体怎么做、拍平是什么意思、最后怎么输出到标签的，一直都不是很明白。本次实验的过程中参考了大量的相关文档，其中 https://xie.infoq.cn/article/c4d84 6096c92c7dfcd6539075 和给了我很大帮助，现在终于对这块儿有了一点更深的理解。

图片分类相关的工作有很多且都很有成效，最近几年也提出了许多更为复杂的神经网络，还需努力学习。图片分类对内容安全具有很重要的意义。